Fast Tempo, Wide Pitch

In the previous section we examined melody’s home range–its size, and melody’s hangouts within it. One facet of melody we discussed was that it tends to remain in a cage, called the tessitura, and I am suggesting that the top and bottom of the tessitura correspond to the Doppler pitches when the fictional mover is directed toward and away from you, respectively. But remember that Doppler shifts are greater when the mover has greater speed. A car driving past you at a crawl will have a small difference between its high approaching pitch and its low moving‑away pitch. But if you stand at the side of the freeway, the difference in pitch as the cars pass you will be much greater. It follows from these simple observations that faster‑tempo pieces of music should have bigger home ranges for their melodies. That is, if melodic contour has been culturally selected to mimic the Doppler shifts of movers, then the prediction is that music with a faster tempo (more beats per minute) should have a wider tessitura.

To test this, Sean Barnett and I measured the tempo and tessitura width of the melodies of all the pieces in the Classical Fake Book (Hal Leonard Corp.). (We did not use the Dictionary of Musical Themes here because it does not include tempo data.) Figure 47 shows how tessitura width varies with tempo (for just those pieces originally intended for keyboard). One can see that although tessitura width does not change for the several low tempos, it rises among the faster tempos. Tessitura width increases with greater tempo, as predicted from the fact that the Doppler pitch home range widens as mover speed increases. This is particularly striking because themes with wider tessituras tend to be more difficult to play, and so one might predict that wider‑tessitura music would go with a slower tempo, but this is the opposite of what we in fact find.

One might wonder whether this result could be due, instead, to a general phenomenon in which faster‑tempo music tends simply to amplify musical qualities, whatever they may be. Caitlin Morris measured the range of loudness levels–the “loudness‑tessitura” width–and the tempo for a sample of 55 pieces in Denes Agay’s piano anthology, The Classical Period. Figure 48 shows how the width of the loudness range varies with tempo, and one can see that there is no trend. The pitch tessitura width does not, then, increase in Figure 47 merely because of some general proclivity to amplify musical qualities at higher tempos. In fact, the lack of change in “loudness‑tessitura” width as a function of tempo is something the music‑is‑movement theory does predict, assuming that loudness in music is primarily driven by proximity, as we discussed in detail in the “Nearness versus Stompiness” section of Chapter 4. Imagine that a mover carries out a bout of behavior in your vicinity at low speed. Now imagine this mover is asked to repeat the same bout of behavior, but this time moving much more quickly–that is, at a higher tempo. In each case the mover is, we presume, going through the same sequence of spatial coordinates, and thus the same sequence of distances from the listener. And so it immediately follows that the mover courses through the same sequence of loudnesses no matter whether moving slowly or quickly. The music‑is‑movement theory predicts, then, that, unlike pitch, the range of loudnesses should not change as a function of the music’s tempo–faster music, same loudness range–and that’s what we found.

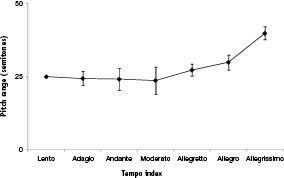
Figure 47 . Tessitura (of melody) width versus tempo, among all 92 pieces for keyboard in the Classical Fake Book for which tempo data could be acquired. One can see that faster music tends to have wider tessituras, consistent with the Doppler interpretation of melodic pitch. (We found the same result when we used the data for all pieces.) The Classical Fake Book was used for two reasons. First, it is helpful because fake books are not cluttered with the notes from the chords (chords are notated via letter labels). Second, it is the only classical fake book I possess, so it amounted to an easy‑to‑get, unbiased sample.

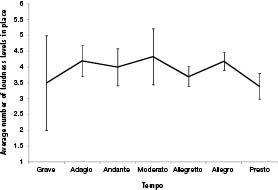
Figure 48 . “Loudness‑tessitura” width (i.e., the total range of loudness levels) versus tempo, sampled from 55 pieces in Denes Agay’s An Anthology of Piano Music, Vol. II: The Classical Period (used instead of the Dictionary of Musical Themes because the latter does not possess loudness information). Unlike (pitch) tessitura width, which is expected–and does–increase with increasing tempo, the loudness‑tessitura is expected–and does–remain constant. This anthology was chosen because it was the only proper non‑fake, non‑lesson book I possessed at home.

We see, then, that faster‑tempo music behaves like faster‑tempo movers: in each case the range of pitches increases with tempo, and the range of loudnesses does not change. Essentially, these results show us that the physics of movers is found in the structure of music. The upcoming Encore section continues the search for physics in music, and concerns momentum and Newton’s First Law.