Medium Encounters

In the Chapter 4 section titled “Slow Loudness, Fast Pitch,” we saw that loudness varies slowly, consistent with the time scales required for movers to vary their distance from you, the listener. We must be more careful, though. If a mover were a “close talker,” tending to move about uncomfortably close to you, then even small changes in distance could lead to large changes in loudness, due to the inverse square law for loudness and distance. But in real life, more than close encounters, we tend to have medium encounters: the movers we typically listen to tend to be in the several‑ to ten‑meter range, not in the centimeter range, and not in the tens or hundreds of meters range. At “medium” distances, large loudness modulations don’t occur over just one or several steps. They require more steps, plausibly in the range of the approximately 10 beats we found for the average loudness duration in Chapter 4.

Not only are our experiences of movers usually at a “medium” distance, but it seems reasonable to expect that individual bouts of behavior tend to occur at an average “medium” distance. Recall our generic encounters from the section titled “Musical Encounters” in Chapter 4: the “center of mass” of the A‑B‑C‑D cycle of movement would be representative of the average distance of a generic encounter. We see, then, that loudnesses of movers will tend to have a typical value. We therefore expect any piece of music to have a baseline loudness level it spends a disproportionate amount of time at, spending less time at loudness levels farther away from this average. Unlike Doppler pitches, which have a distribution that is fairly broad and flat, the distribution of mover loudnesses tends to be more peaked. Is music like this? Does music spend most of its time at an average loudness level, relatively rarely venture out of that loudness zone, and more rarely still pursue greater loudness deviations from the average? Music is indeed roughly like this. Music tends to use mezzo forte as this baseline, with lesser and greater loudness levels happening progressively more rarely. RPI students Caitlin Morris and Eric Jordan measured the average percentage of a song spent at each of its loudness levels, and the results are shown in Figure 51. One can see that there is a strong “mountain” shape to the plot: pieces tend to spend more time at intermediate loudness levels than at loudness levels deviating far from the central values. (Although our data were broadly consistent with our expectation, there was a slight downward divot at mezzo forte relative to piano and forte , with the greatest percentage of time spent in piano .)

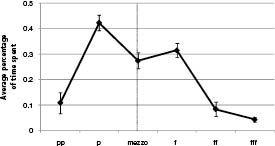
Figure 51 . For each song, the total percentage of time spent at each loudness level was determined. These distributions were then averaged together across 43 pieces in Denes Agay’s An Anthology of Piano Music, Vol. II: The Classical Period .

We can say more. Consider the obvious fact that there is less real estate–less space–near you than far from you. This asymmetry means that a mover has more chances to be farther than average from you than to be nearer than average to you. There should not only be, then, a roughly mountain shape to Figure 51, but the below‑average levels of loudness should be more common than the above‑average levels of loudness. The mountain should have a higher level at lower‑than‑average levels of loudness. The distribution we just plotted in Figure 51 has , in fact, this expected asymmetry.

We can say something further still. Not only should movers spend a greater proportion of their time relatively far away than relatively nearby, but when they do get near, and thus relatively loud, this should be more transient. Why? Because the mover will more quickly leave the near region, for the simple reason that “the near” is an inherently smaller piece of land than “the far.” This is indeed the case, as shown in Figure 52, also obtained by Caitlin Morris and Eric Jordan

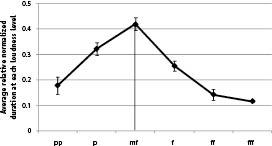
Figure 52 . For each song, the average duration of each loudness level was computed, and then these per‑song average normalized so that the sum across the levels equaled one. Then, these were averaged across 43 pieces measured in Denes Agay’s An Anthology of Piano Music, Vol. II: The Classical Period . One can see the asymmetry. As predicted from the spatial asymmetries of near and far, music should tend to have longer durations at lower‑than‑average loudness levels compared to higher‑than‑average loudness levels.

We see, then, that loudnesses distribute themselves as expected if they are about proximity. Encounters have a typical distance; more cumulative time is spent farther than nearer; and nearer segments of encounters tend to be short‑lived relative to farther segments.