Synchronous Generator Performance

In open-circuit conditions when the stator (armature) winding is open and the generator does not supply power to a load, there is no current in the stator winding. The magnetic flux produced by the field current induces an emf in the three-phase stator winding.

In closed-circuit conditions when the generator operates into a load, a current flows in the stator winding. At a balanced load, the ar­mature (stator) currents are equal in magnitude and shifted in phase by one-third of a period (120°). The armature currents produce a magnetic field revolving at a speed n₁ = 60f/p = n, i.e. this field revolves in synchronism with the field of the rotor winding. The emf induced in the stator winding depends on the magnetic flux of the poles. If the magnetic flux is small, the emf is also small, and vice versa. At a constant speed of the rotor, the emf is proportional to the magnetic flux excited by the direct current flowing in the field winding. An increased current in the field winding produces a stronger magnetic flux, which results in a higher emf. Consequently, since the emf varies with the field current, it is possible to control the voltage at generator terminals by properly changing the field current.

In open-circuit conditions, the voltage across the generator ter­minals is equal to the emf generated in the armature. In the loaded generator, the voltage is not equal to the emf because of the voltage drop across the resistance and reactance of the stator winding. Be­sides, the currents flowing through the stator winding produce the armature reaction flux which acts on the flux of the field winding, so that the magnetic flux under load is not equal to the magnetic flux at no load. That is why, changes in the load, i.e. changes in the armature current, will cause changes in the terminal voltage if the field current remains constant.

In Fig. 7.15a are shown the external characteristics of a synchro­nous generator at resistive and reactive loads. These characteristics are the plots of the terminal voltage as a function of the load cur­rent at a constant rotor speed and constant field current. What ac­counts for the different shapes of the curves at resistive, inductive, andcapacitive loads is a nonuniform action of the armature reaction field on the flux of poles.

Any load requires a constant line voltage for its normal operation. The line voltage is kept constant with changes in the load on the generator by changing the field current.

Figure 7.15b illustrates the control characteristics which are the plots of field current versus load current at a constant line voltage. They actually show the range over which it is necessary to change the field current with changes in the load current in order to main­tain the terminal voltage constant. At a resistive load, an increase in the armature current causes a slight dip in the voltage because the armature reaction decreases the magnetic flux to a small degree. This load calls for an insignificant increase in the field current to keep the voltage invariable. At an inductive load, an opposing armature reaction field appears, which reduces the flux of poles. The field current now need be higher, than it is in the previous case, to compensate for the opposing armature reaction field and, thus, to obtain a constant net flux which induces a constant voltage. At a capacitive load, the magnetic flux grows, so the field current must be reduced to decrease the armature current and, thus, provide for the constant voltage.

Synchronous generators most often operate into a common external circuit, of a power plant or a power system. The voltage V_c and fre­quency of such a power circuit are invariable. The voltage V_g across

the generator terminals is equal and opposite to the circuit voltage, V_g = –V_c. The net armature flux Ф_n revolving at a speed n₁ = = 60f/p in space leads the voltage V_g by 90° (Fig. 7.16).

With the power circuit voltage V_c invariable, the amplitude of the net armature flux Ф_nremains invariable too. At a resistive load on the generator, the armature current I is in phase with V_g. The armature reaction flux Ф_а is in phase with I, so their phasors that only differ in length are laid on the same axis. The net magnetic flux is the phasor sum of the field winding flux Ф_m (flux of poles) and the armature reac­tion flux Ф_а.

A change in the field current does not change the active power of the generator since the power it receives from the prime mover is constant (the torque of the prime mover and its speed are constant). Therefore, the active component of the arma­ture current is constant and the head of phasor I (Ф_а) rests on the straight line AB parallel to the x-axis. Increasing the field current causes an increase in the field winding flux whose phasor Ф'_т lies between the line А В and the head of the invariable phasor Ф_n. In this case, the phasor I' (Ф'_а) will change both in magnitude and in direction, i.e. the current will lag the generator voltage in phase. 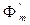As the field current decreases, so too does the flux , which will cause the armature current I" ( 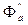) to change both in magnitude and in phase. Thus, variations in the field current of the generator operating into a power network lead to variations in the reactive component of the armature current, i.e. in the reactive power produced by the generator.

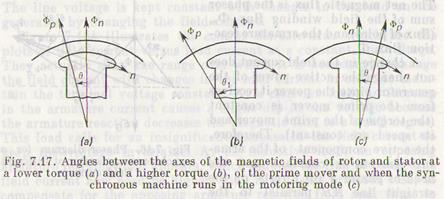
For the active power to be changed, it is necessary to change the torque of the prime mover driving the generator rotor. The torque T₁ of the prime mover causes the generator rotor to revolve at a speed n in a minute. The net armature field revolves at the same speed, n₁ = n (Fig. 7.17a). Consequently, the field Ф_m excited by the; field winding and the net armature field Ф_n rotate in synchronism and, thus, remain stationary with respect to each other and interact in a definite manner. As a result, there appears an electromagnetic brak­ing torques T_e that counterbalances the prime mover torque. When these torques are equal, T₁= T_e, the angle Э between the axes of the magnetic fields remains invariable.

Should the torque T'₁ exceed the torque T'_e, the rotor begins to accelerate to a speed in excess of the constant speed of the revolving armature field, n₁ = 60 f/p, where f is the constant line frequency (Fig. 7.17b). The angle θ₁ between the axes of the magnetic fields of the rotor and stator will then grow, thereby causing the torque T'_e to rise until it becomes equal to T'₁.

When a synchronous machine runs as a motor, the angle θ between the axes of magnetic fields is such as illustrated in Fig. 7.17c.

Before switching a generator into a power line, one must ensure that the line and generator have the same sequence of phases and the line voltage and frequency are equal to the generator emf and

frequency. Besides, at the instant of switching, the generator emf in each phase must be opposite in direction to the line voltage. If these conditions are not met, large currents may appear, which would render the generator inoperative. Special devices called synchronoscopes are used to connect generators into power lines. A simple synchronoscope consists of three incandescent lamps designed for double line voltage and connected across the terminals of the gene­rator and power line. With the generator terminals disconnected from the line, the lamps come on and go out simultaneously. At the instant when the generator emf is equal in magnitude but opposite in direction to the line voltage, the lamps get dark because the vol­tage across each lamp is zero. The generator is now ready for switch­ing into the line. The generator emf read on the voltmeter is set equal to the line voltage by adjusting the field current. The genera­tor frequency is controlled by changing the rotational speed of the prime mover.

7.13. Synchronous Motors

A synchronous motor does not principally differ in design from a synchronous generator. As with the generator stator, the stator of the motor carries a three-phase winding which, when connected to a three-phase line, provides for the magnetic field revolving at a speed n₁ = 60 f/p in a minute. The field winding arranged on the rotor receives direct current from a rectifier or an exciter mounted on the same shaft as the rotor. The field (excitation) current produces the magnetic flux Ф_m of the rotor. The net magnetic field Ф_п excited by the stator current tends to carry along the rotor poles in the direc­tion of its rotation as illustrated in Fig. 7.17c. The rotor can turn at precisely synchronous speed equal to the rotational speed of the stator field. The speed of a synchronous motor is thus strictly con­stant if the power line frequency is invariable.

The main advantage of a synchronous motor is that it can operate on a leading current, i.e. it can act as a capacitive load for the power line. Such a motor raises cosφ of the entire network as it makes up for the reactive power of other loads of the consumer.

As in a generator, the reactive power (cosφ) of a motor is varied by adjusting the field current. At a certain field current corresponding to rated excitation, the power factor cosφ is unity. A decrease in the field current gives rise to lagging (inductive) current in the stator; an increase in the field current that overexcites the motor causes a leading (capacitive) current to appear in the stator.

An advantage of this motor over an induction counterpart is that it is less sensitive to changes in the supply voltage. In the former, the torque is proportional to the line voltage raised to the first pow­er, whereas in the latter, it varies as the square of the volt­age.

The torque results from the interaction of the magnetic fields of rotor and stator. It is only the magnetic flux of the stator field that depends on the line voltage.

Synchronous motors largely come in salient pole designs, nor­mally operated on a leading current at cosφ = 0.8, with the field current supplied from exciters or from ac circuits via semiconductor rectifiers.

The synchronous motor connected to the supply line cannot produce the starting torque. With the rotor stationary, the revolv­ing stator field travels at synchronous speed with respect to the ro­tor field and, hence, does not interact with the rotor field. To start the motor, the rotor should first be set in motion to enable it to acce­lerate to or almost to the synchronous speed.

The motor is made self-starting through induction-motor action provided by a squirrel-cage winding (damper winding) inserted in the rotor pole faces. With the stator winding connected to the three-phase power line, the motor starts on the cage winding, just like an ordinary squirrel-cage motor. As the motor comes up almost to syn­chronous speed (95% of this speed), the exciter is cut in to supply the field winding. The torque developed is now enough to pull the rotor into synchronism.

At starting, the field winding must be closed through a resistance that is 10 to 12 times the resistance of the winding itself. This win­ding must not be left open or short-circuited during the starting per­iod. Should it prove open, the stator field would cut the conductors of the field winding at a great rate and induce a large emf in the winding, which may cause breakdown of its insulation and, thus, offer a hazard to attendants. Should the field winding be shorted out when starting the motor under load, the rotor would accelerate nearly to half the synchronous speed and fail to pull into synchro­nism.

The operation of a synchronous machine on a leading current makes this machine suitable for use as a synchronous capacitor. The synchronous capacitor is a synchronous machine running without load and designed to improve the power factor of the ac system. It supplies reactive power to the ac system and insignificantly differs in design from an ordinary synchronous motor. Since the former car­ries no load, its shaft and rotor are lighter than those of the latter and its air gap is smaller.

The basic disadvantage of a synchronous motor is that it requires an ac and a dc source for its operation. The need to supply direct current to the field winding makes this motor rather inefficient at low powers. That is why, low-power synchronous motors with dc excitation do not find any use. Reluctance motors enjoy wide appli­cation where power demands are low. The rotor of this type of syn­chronous motor has salient poles. For motors of very small powers, the rotor is made cylindrical. It is cast from aluminum in the mold with soft iron cores inserted into it to form salient poles. The cy­lindrical shape facilitates the rotor machining and balancing and also reduces the windage loss, which is of importance for small-pow­er motors.

In a reluctance motor, the rotor develops the torque by virtue of its orientation in the magnetic field in such a way that the reluctance offered to the field is the lowest. The rotor always takes a definite position in space, such that the magnetic lines of the revolving stator field continue through the rotor iron and the rotor normally operates at the synchronous speed of the stator field.

REVIEW QUESTIONS

1. Explain the operation principle of an induction motor.

2. How can one reverse the sense of rotation of an induction motor?

3. Give the basic features of the construction of an induction motor with a wound rotor and with a squirrel-cage rotor.

4. What factors affect the torque of an induction motor?

5. Draw the operating characteristics of an induction motor.

6. Explain how to start a three-phase induction motor and to control its speed.

7. Describe the synchronous generator action and construction.

8. What relations do the external and control characteristics of a synchronous generator reveal?

9. What conditions must be complied with before connecting a synchronous generator across the power line?

10. Explain the operation principle of a synchronous motor.