Проточный реактор идеального смешения в неизотермическом режиме
При составлении балансовых уравнений в качестве элементарного объема для реактора идеального смешения принимают полный реакционный объем V. Тепловые потоки за элементарный промежуток времени dτ для объема V:
 ; (6.3)
; (6.3)
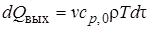 ; (6.4)
; (6.4)
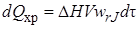 ; (6.5)
; (6.5)
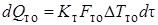 , (6.6)
, (6.6)
где cp – средняя теплоемкость реакционной смеси; ρ – средняя плотность реакционной смеси; ∆H – тепловой эффект реакции, отнесенный к 1 моль реагента; Кт – коэффициент теплопередачи; Fто– поверхность теплообмена с окружающей средой; ∆Тто – движущая сила теплообмена (средняя разность температур в реакторе и внешней среде, с которой происходит теплообмен); величины, относящиеся к входному потоку, отмечены индексом «0», величины без индекса относятся к реакционной смеси, находящейся в реакторе в данный момент или выходящей из него.
Накопление теплоты в реакторе за время dτ равно изменению теплосодержания реакционной смеси:
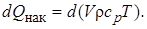 (6.7)
(6.7)
С учетом уравнений (6.2)–(6.7) уравнение теплового баланса для нестационарного режима будет иметь вид
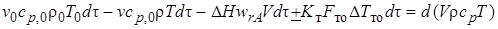
или
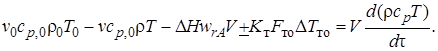 (6.8)
(6.8)
В стационарном режиме правая часть уравнения (6.8) равна нулю. Если также принять, что v0 = v и пренебречь изменением средней теплоемкости и плотности реакционной смеси при изменении состава и температуры, для стационарного режима
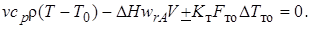 (6.9)
(6.9)
Математическая модель неизотермического реактора идеального смешения кроме уравнения теплового баланса (6.9) включает в себя уравнение материального баланса
 . (6.10)
. (6.10)
Уравнения (6.9) и (6.10) взаимосвязаны: в оба входит в качестве составной части функция wrA(cA, T). Скорость химической реакции wrA зависит и от концентрации реагентов (степени превращения), и от температуры. Чем выше температура, тем выше скорость реакции и, следовательно, тем большая степень превращения должна достигаться при том же среднем времени пребывания  . Но рост степени превращения автоматически должен приводить к понижению скорости реакции. В проточном реакторе заданного объема устанавливаются степень превращения и температура, которые одновременно должны удовлетворять и уравнению (6.9), и уравнению (6.10).
. Но рост степени превращения автоматически должен приводить к понижению скорости реакции. В проточном реакторе заданного объема устанавливаются степень превращения и температура, которые одновременно должны удовлетворять и уравнению (6.9), и уравнению (6.10).
При совместном решении уравнений (6.9) и (6.10)при заданных
 = V/v и начальной температуре Т0можно определить значения хА и Т, удовлетворяющие этим уравнениям. Ниже рассмотрен анализ возможных решений уравнений материального и теплового балансов сначала для адиабатического реактора идеального смешения, затем для реактора идеального смешения с внешним теплообменом. На основании этого анализа можно сделать вывод о том, какие условия проведения процесса нужно выбрать для достижения высокой степени превращения реагентов.
= V/v и начальной температуре Т0можно определить значения хА и Т, удовлетворяющие этим уравнениям. Ниже рассмотрен анализ возможных решений уравнений материального и теплового балансов сначала для адиабатического реактора идеального смешения, затем для реактора идеального смешения с внешним теплообменом. На основании этого анализа можно сделать вывод о том, какие условия проведения процесса нужно выбрать для достижения высокой степени превращения реагентов.
Совместное решение уравнений материального и теплового балансов для стационарного адиабатического реактора идеального смешения.Математическая модель проточного адиабатического реактора идеального смешения представляет собой систему уравнений материального и теплового балансов:
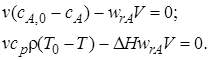 (6.11)
(6.11)
Определим, используя эту систему уравнений, степень превращения хА и температуру Т,достигаемые в реакторе. Различные частные решения зависят от конкретного вида кинетического уравнения wrA = wrA(cA, T) реакции, протекающей в аппарате. Рассмотрим решения для реакций с наиболее простой кинетикой: необратимой реакции первого порядка А 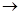 R и обратимой реакции первого порядка А
R и обратимой реакции первого порядка А  R, так как в этих случаях все математические выкладки проще.
R, так как в этих случаях все математические выкладки проще.
Предварительно преобразуем систему уравнений (6.11). В уравнении материального баланса заменим изменение концентраций (сА,0 – cА) равным ему соотношением сА,0 хА. Упростим уравнение теплового баланса, исключив из него скорость реакции wrA.
Для этого воспользуемся уравнением материального баланса, в соответствии с которым wrAV = v(cA,0 – сА) = vcА,0xA. Тогда уравнение теплового баланса примет вид vcpρ(Т0 – Т) – ∆HvсА,0хА = 0. После сделанных преобразований систему уравнений (6.11)запишем так:
 (6.12)
(6.12)
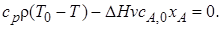 (6.13)
(6.13)
Необратимая реакция первого порядка. Кинетическое уравнение необратимой реакции первого порядка имеет вид
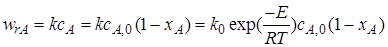 .
.
Подставим его в уравнение (6.12)
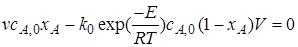 . (6.14)
. (6.14)
Для определения степени превращения хА и температуры Т в реакторе уравнение материального баланса (6.14)нужно решить совместно с уравнением теплового баланса (6.13). Аналитическое решение этой системы уравнений затруднено из-за того, что температура T входит в уравнения и в виде линейного члена, и в составе комплекса, являющегося показателем экспоненциальной функции. Такие уравнения являются трансцендентными, и для их решения применяют численные методы.
Решим систему уравнений (6.13) и (6.14)графическим методом. Для этого запишем оба уравнения в виде зависимостей хА Т,построим графики этих зависимостей и найдем точки их пересечения, удовлетворяющие одновременно обоим уравнениям, т. е. являющиеся решениями системы.
В уравнении теплового баланса (8.14)зависимость между хА и T является линейной.
Эта прямая линия пересекает ось температур в точке Т = Т0и имеет угловой коэффициент
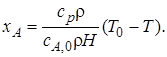 (6.15)
(6.15)
Знак углового коэффициента зависит от знака теплового эффекта, он отрицателен для эндотермических реакций, у которых ∆Н > 0 (рис. 6.1, а),и положителен для экзотермических реакций (рис. 6.1, б). Крутизну угла наклона можно изменить, меняя начальную концентрацию сA,0.

Рис. 6.1. Уравнение теплового баланса реактора идеального смешения
в координатах хА – Т дляэндотермической (а)и экзотермической (б)реакций
Если принять хА = 1 (т. е. реакция прошла до конца), из уравнения (6.15) получим
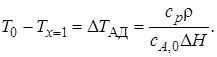
Величина ∆TАД – максимальное изменение температуры реакционной смеси, возможное в адиабатических условиях, или адиабатическое изменение температуры (для экзотермических реакций, например, адиабатический разогрев). Уравнение (6.15) с учетом ∆Tадможно записать так:
 (6.16)
(6.16)
Вид зависимости хА(T), соответствующей уравнению материального баланса (6.12), зависит от типа кинетического уравнения реакции. Для необратимой реакции первого порядка (эндотермической, и экзотермической) уравнение материального баланса (6.12) можно представить в следующем виде (с учетом того, что V/v =  ):
):
 (6.17)
(6.17)
Уравнение (6.17) описывает монотонно возрастающую функцию хa(T). При низких температурах, когда кинетическая энергия молекул существенно ниже энергии активации (об этом можно судить, сравнивая энергии Е и RT), хА 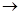 0. При высоких температурах, когда величины Е и RT имеют одинаковый порядок, числовое значение exp[E/(RT)]невелико. Так как предэкспоненциальный множитель k0= 108 + 1013, то в этом случае хА
0. При высоких температурах, когда величины Е и RT имеют одинаковый порядок, числовое значение exp[E/(RT)]невелико. Так как предэкспоненциальный множитель k0= 108 + 1013, то в этом случае хА 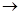 1.
1.
Таким образом, график функции (6.17) – кривая без экстремумов (рис. 6.2, кривая 1), при низких температурах асимптотически приближающаяся к нулю, при высоких – к единице, а при «средних» температурах имеющая одну точку перегиба (ее координаты можно получить, приравняв нулю производную d2xA/dT2).
Положение среднего участка кривой относительно оси температур можно изменить, увеличив или уменьшив среднее время пребывания в реакторе  (
(  = V/v). Из уравнения (6.17) следует, что увеличение
= V/v). Из уравнения (6.17) следует, что увеличение  при тех же температурах приведет к росту хА (рис. 6.2, кривая 2).
при тех же температурах приведет к росту хА (рис. 6.2, кривая 2).
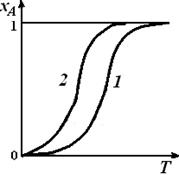
Рис. 6.2. Уравнение материального баланса реактора идеального смешения в координатах хA – Т для необратимой реакции первого порядка
при среднем времени пребывания 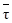 1 (1)и
1 (1)и 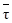 2 (2)
2 (2)
Решение системы уравнений материального и теплового балансов имеет несколько различающийся вид для эндо- и экзотермических необратимых реакций. В случае проведения в адиабатическом реакторе идеального смешения необратимой эндотермической реакции графики функций (6.16) и (6.17) имеют лишь одну точку пересечения (см. рис. 6.3).
Координаты этой точки (хА/, T/) и являются решением системы уравнений: если в адиабатический реактор идеального смешения заданного объема V подает исходный реагент А, имеющий концентрацию сА,0 с объемным расходом v и при начальной температуре Т0,необратимая эндотермическая реакция будет протекать в аппарате при температуре Т и при этом будет достигаться степень превращения хА/.

Рис. 6.3. Уравнения теплового (1) и материального (2)балансов
для адиабатического реактора идеального смешения при проведении
в нем необратимой эндотермической реакции (совместное решение)
Если в адиабатическом реакторе проводят необратимую экзотермическую реакцию, система уравнений материального и теплового балансов может иметь как одно, так и несколько решений, отвечающих стационарному режиму.
Из рис. 6.4 видно, что графики функций (6.16) и (6.17) имеют только одну точку пересечения, если начальная температура Т0реакционного потока будет сравнительно низкой (например, Т10)или сравнительно высокой (например, T20). При этом оказывается, что при подаче реагентов в реактор с низкой начальной температурой Т10процесс будет протекать при температуре, мало отличающейся от T10, а достигаемая степень превращения (ордината точки А на рис. 6.4) также будет очень низка. Более выгодным является режим работы реактора, соответствующий начальной температуре Т30.В этом случае также имеется лишь одна точка пересечения графиков (точка Е),т. е. одно решение системы уравнений, но оно соответствует высокой степени превращения, почти равной единице.
Если же реагенты подавать в реактор с начальной температурой Т20, то линии, соответствующие уравнениям материального и теплового балансов, пересекаются трижды, т. е. координаты точек В, С, D являются возможными решениями системы уравнений, составляющей математическую модель адиабатического реактора идеального смешения.
В таких случаях говорят о множественности стационарных состояний реактора. При этом возникает дополнительная проблема устойчивости рассматриваемых стационарных состояний.
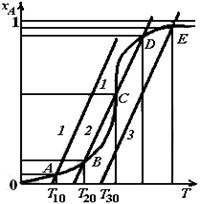
Рис. 6.4. Уравнения теплового (1, 2, 3) и материального (4)балансов
для адиабатического реактора идеального смешения при проведении
в нем необратимой экзотермической реакции (совместное решение)
Обратимая реакция первого порядка.Для обратимой реакции первого порядка А 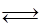 R кинетическое уравнение имеет вид
R кинетическое уравнение имеет вид
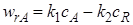 . (6.18)
. (6.18)
Выразив в уравнении (6.18) концентрации сА и сR через сА,0 и хА получим

В условиях равновесия для обратимой реакции первого порядка имеет место равенство скоростей прямой и обратной реакции  ,откуда следует, что
,откуда следует, что
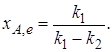 (6 19)
(6 19)
С учетом выражения (6.19) кинетическое уравнение обратимой реакции первого порядка примет вид
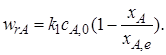 (6.20)
(6.20)
После подстановки выражения (6.20) в формулу (6.12) уравнение материального баланса можно представить в виде зависимости хА от Т:
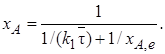 (6.21)
(6.21)
Уравнение (6.21), как и следовало ожидать, при хА,е = 1 (т. е. для необратимой реакции первого порядка) переходит в уравнение (6.17).
Для графического решения системы уравнений материального и теплового балансов в случае обратимой реакции нужно построить график функции (6.21). График уравнения теплового баланса (6.15), не содержащего никаких кинетических параметров реакции, от вида кинетического уравнения не зависит.
В уравнении (6.21) от температуры зависят константа скорости прямой реакции k1, и равновесная степень превращения хА,е.
Для обратимой эндотермической реакции (∆H > 0) с ростом температуры увеличивается и константа равновесия, и равновесная степень превращения. Величина хА,рассчитанная по уравнению (6.21), при любых температурах будет меньше, чем k1, 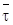 , и меньше, чем хА,е, т. е. грфик функции хА(Т)должен находиться на координатной плоскости (рис. 6.5, a) ниже графиков функций k1(Т)
, и меньше, чем хА,е, т. е. грфик функции хА(Т)должен находиться на координатной плоскости (рис. 6.5, a) ниже графиков функций k1(Т) 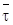 и хА,e(Т).
и хА,e(Т).
Система уравнений материального и теплового балансов для обратимой экзотермической реакции имеет такой же вид, как и для обратимой эндотермической реакции, т. е. это уравнения (6.21) и (6.15). Однако график функции хА(Т),определяемый уравнением (6.21), будет другим. Связано это с тем, что равновесная степень превращения хА,е для экзотермических реакций с ростом температуры падает. Поэтому, построив график функции хА(Т),пользуясь при этом теми же приемами, что и для обратимой экзотермической реакции, получим кривую с максимумом (рис. 6.5, б). Абсолютное значение максимума и его положение относительно кривой определяются, с одной стороны, средним временем пребывания реагентов в реакторе τ, а с другой – состоянием химического равновесия.
Уравнение теплового баланса – прямая 1 с положительным тангенсом угла наклона. Эта прямая может пересекаться с кривой 2, отвечающей уравнению материального баланса, в одной или в нескольких точках (одно или несколько стационарных состояний).

Рис. 6.5. Уравнения теплового (1) и материального (2)балансов
для адиабатического реактора идеального смешения при проведении
в нем обратимых эндотермической (а)и экзотермической (б)реакций
(совместное решение)
Способы увеличения степени превращения реагентов при проведении реакций в адиабатическом реакторе идеального смешения.Взависимости от начальных условий (температуры на входе Т0,начальной концентрации сА,0), соотношения объема аппарата и объемного расхода ( 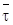 = V/v),а также типа химической реакции в проточном реакторе идеального смешения устанавливается некоторое стационарное состояние, характеризующееся неизменяющимися во времени значениями температуры реакционной смеси и степени превращения на выходе из аппарата. Эти значения T и xA могут быть определены на основании совместного решения уравнений материального и теплового балансов, как это было показано выше.
= V/v),а также типа химической реакции в проточном реакторе идеального смешения устанавливается некоторое стационарное состояние, характеризующееся неизменяющимися во времени значениями температуры реакционной смеси и степени превращения на выходе из аппарата. Эти значения T и xA могут быть определены на основании совместного решения уравнений материального и теплового балансов, как это было показано выше.
В промышленных условиях очень важно наиболее полно использовать исходное сырье, т. е. достичь высоких значений степени превращения. Анализ получающихся решений позволяет найти условия проведения процесса, при которых достигается оптимальная степень превращения реагентов в адиабатическом реакторе идеального смешения.
Графическое решение системы уравнений материального и теплового балансов сводится к определению точки пересечения графиков функций хА(Т),отвечающих и тому, и другому уравнениям. Более высокая степень превращения исходного сырья в адиабатическом реакторе соответствует на рис. 6.3–6.5 смещению точки пересечения в область больших значений хА. Добиться этого можно, изменяя взаимное положение кривой, отвечающей уравнению материального баланса, и прямой, соответствующей уравнению теплового баланса. Укажем возможные способы влияния на положение этих линий.
Для эндотермических реакций (необратимых и обратимых) повышения степени превращения можно добиться, прежде всего, увеличением начальной температуры T0, что приведет к параллельному смещению вправо прямой 1 (см. рис. 6.3 и 6.5, а).
Для необратимых экзотермических реакций увеличение температуры на входе в реактор также приведет к росту степени превращения (см. рис. 6.4, прямая 2). Одновременно это позволит избежать тройного пересечения линий 2 и 4,отвечающего случаю множественности стационарных состояний. Однако увеличение начальной температуры должно быть оправдано экономическими соображениями, так как рост степени превращения будет сопровождаться при этом и увеличением затрат на нагрев исходной реакционной смеси.
Для обратимых экзотермических реакций, проводимых в адиабатическом реакторе идеального смешения, целесообразно добиться таких условий, чтобы решение системы уравнений материального и теплового балансов соответствовало точке максимума линии 2,отвечающего уравнению материального баланса (см. рис. 6.5, б). Смещение прямой 1 вправо при возрастании начальной температуры может привести не к увеличению, а к уменьшению степени превращения. Выбор оптимальных условий проведения обратимых экзотермических реакций представляет наибольшую сложность.
Другой способ изменения положения прямой, отвечающей уравнению теплового баланса, состоит в изменении угла ее наклона. Угловой коэффициент прямой, описываемой уравнением (6.15), можно увеличить или уменьшить, изменив начальную концентрацию сА,0:
 .
.
В эндотермических реакциях для повышения хA при сохранении прежней начальной температуры нужно увеличить крутизну прямой, что можно сделать уменьшением сA,0 (это не всегда целесообразно, так как придется работать с низко концентрированными реагентами). При проведении экзотермических реакций увеличение сА,0 приведет к росту ∆Тад, и прямая станет более пологой.
Повышение степени превращения хА может быть достигнуто также при увеличении среднего времени пребывания 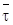 = V/v. Во всех рассмотренных случаях на графиках (см. рис. 6.3–6.5) произойдет смешение влево линии, отвечающей уравнению материального баланса. При проведении обратимых реакций положение этой линии ограничено условиями равновесия [зависимость хА,е(T)]. Поэтому добиться увеличения хА можно изменением условий, влияющих на равновесие.
= V/v. Во всех рассмотренных случаях на графиках (см. рис. 6.3–6.5) произойдет смешение влево линии, отвечающей уравнению материального баланса. При проведении обратимых реакций положение этой линии ограничено условиями равновесия [зависимость хА,е(T)]. Поэтому добиться увеличения хА можно изменением условий, влияющих на равновесие.
В каждом конкретном случае проводится анализ всех возможных способов увеличения степени превращения с проведением технико-экономического сравнения.
Стационарный неадиабатический реактор идеального смешения.Для расчетов реактора идеального смешения, работающего в промежуточном тепловом режиме, пользуются полным уравнением теплового баланса (6.9)
 .
.
Движущей силой теплообмена ∆Tто между реакционной смесью, находящейся в реакторе, и теплоносителем (внешней средой) является средняя разность температур реакционной смеси и теплоносителя. Температура реакционной смеси Т одинакова в любой точке аппарата идеального смешения. Если считать, что средняя температура теплоносителя Тт,то ∆Tто = |Tт – Т |.
Рассмотрим проведение экзотермической реакции в реакторе идеального смешения с отводом теплоты. Тогда Т > Тти уравнение (6.9) с учетом уравнения материального баланса можно записать так:
 (6.22)
(6.22)
Преобразуем уравнение (6.22)к виду хА = хА(T), чтобы сделать возможным графическое решение системы уравнений материального и теплового балансов (рис. 6.6):
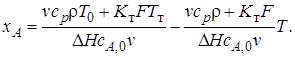 (6.23)
(6.23)

Рис. 6.6. Уравнения материального и теплового балансов для неадиабатического реактора идеального смешения при проведении необратимой экзотермической реакции (совместное решение): линии уравнения теплового баланса: 1 – для адиабатического реактора; 2 – для реактора с отводом теплоты; штриховая – для изотермического реактора; 3 – линия уравнения материального баланса
Уравнение (6.23) – уравнение прямой, как и уравнение теплового баланса (6.15) адиабатического реактора идеального смешения, но с большим свободным членом и большим угловым коэффициентом. Поэтому прямая, описываемая им, смещена относительно линии уравнения теплового баланса адиабатического реактора и имеет большую крутизну (линия 2).
Аналогичные рассуждения подходят для проведения эндотермических реакций в реакторах с подводом теплоты.
Предельным случаем неадиабатического реактора является изотермический аппарат, в котором вся теплота реакции компенсируется теплообменом с внешней средой. Уравнение теплового баланса для изотермического реактора изобразится прямой линией, параллельной оси ординат (Т = Т0)– штриховая линия.
Дата добавления: 2015-06-17; просмотров: 4441;
