Реактор идеального вытеснения
Реактор идеального вытеснения представляет собой длинный канал, через который реакционная смесь движется в поршневом режиме (рис. 5.4). Каждый элемент потока, условно выделенный двумя плоскостями, перпендикулярными оси канала, движется через него как твердый поршень, вытесняя предыдущие элементы потока и не перемешиваясь ни с предыдущими, ни со следующими за ним элементами.
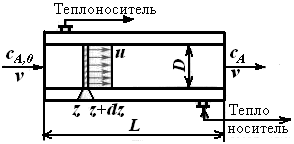
Рис. 5.4. Схема реактора идеального вытеснения
Естественно, что при проведении химической реакции, например реакции, в которой участвуют два или более реагентов, перемешивание участников реакции является необходимым условием ее осуществления, иначе невозможным будет контакт между разноименными молекулами, в результате которого и происходит элементарный акт реакции. Если в реакторе идеального смешения перемешивание носит глобальный характер и благодаря ему параметры процесса полностью выравниваются по объему аппарата, в реакторе идеального вытеснения перемешивание является локальным: оно происходит в каждом элементе потока, а между соседними по оси реактора элементами, как уже указывалось, перемешивания нет.
Идеальное вытеснение возможно при выполнении следующих допущений: 1) движущийся поток имеет плоский профиль линейных скоростей; 2) отсутствует обусловленное любыми причинами перемешивание в направлении оси потока; 3) в каждом отдельно взятом сечении, перпендикулярном оси потока, параметры процесса (концентрации, температуры и т. д.) полностью выравнены.
Следует отметить, что строго эти допущения в реальных реакторах не выполняются. Из гидравлики известно, что даже в очень гладких каналах при движении потока, характеризующегося высокими числами Рейнольдса Re, у стенок канала существует так называемый пограничный вязкий подслой, в котором градиент линейной скорости очень велик. Сравнивая профили скоростей при различных потоках (рис. 5.5), видно, что максимально приблизиться к идеальному вытеснению можно лишь в развитом турбулентном режиме.
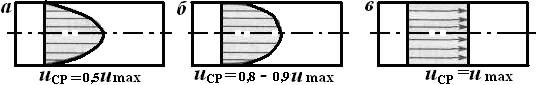
Рис. 5.5. Профили линейных скоростей потока при ламинарном (а),развитом турбулентном (б) и идеальном поршневом (в)режимах течения жидкости
Однако турбулентный поток характеризуется наличием нерегулярных пульсаций, носящих хаотичный характер, в результате чего некоторые частицы потока могут опережать основной поток или отставать от него, т. е. произойдет частичное перемешивание в осевом направлении. Конечно, абсолютные значения таких перемещений будут невелики по сравнению с основным осевым перемещением потока, и при больших линейных скоростях ими можно пренебречь. В то же время турбулентные пульсации в радиальном направлении будут способствовать локальному перемешиванию реагентов и выполнению третьего допущения.
В реальном реакторе можно приблизиться к режиму идеального вытеснения, если реакционный поток – турбулентный и при этом длина канала существенно превышает его поперечный размер (например, для цилиндрических труб L/D > 20).
В соответствии с принятыми допущениями общее уравнение материального баланса (4.7) для элементарного объема проточного реактора можно упростить. Прежде всего, в качестве элементарного объема в этом случае можно рассматривать объем, вырезанный двумя параллельными плоскостями, находящимися друг от друга на бесконечно малом расстоянии dz и перпендикулярными оси канала z (см. рис. 5.4).
В этом элементарном объеме в соответствии с третьим допущением 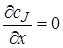 и
и 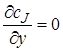 . Следовательно, конвективный перенос происходит только в направлении оси z. В соответствии со вторым и третьим допущениями диффузионный перенос в реакторе идеального вытеснения отсутствует (как и в реакторе смешения). Следовательно, уравнение (4.7) для реактора идеального вытеснения в нестационарном режиме работы примет вид
. Следовательно, конвективный перенос происходит только в направлении оси z. В соответствии со вторым и третьим допущениями диффузионный перенос в реакторе идеального вытеснения отсутствует (как и в реакторе смешения). Следовательно, уравнение (4.7) для реактора идеального вытеснения в нестационарном режиме работы примет вид
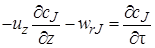 . (5.9)
. (5.9)
Из уравнения (5.9) видно, что в нестационарном реакторе идеального вытеснения концентрация реагента реакции сJ является функцией двух переменных: координаты z и времени τ. При стационарном режиме уравнение будет еще более простым (в этом случае концентрация является только функцией координаты z):
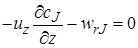 . (5.10)
. (5.10)
В реакторе с постоянной площадью поперечного сечения канала линейная скорость потока uz будет величиной постоянной, равной отношению объемного расхода v к площади сечения F(uz= v/F). Тогда, с учетом того, что Fz/v = V/v =  , уравнение (5.10)можно записать в таком виде:
, уравнение (5.10)можно записать в таком виде:
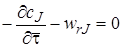 . (5.11)
. (5.11)
Следует еще раз обратить внимание на то, что величина  (среднее время пребывания реагентов в проточном реакторе, характеризующее для реактора вытеснения продолжительность прохождения потоком расстояния от входа в реактор до некоторой точки z на оси реактора) по физическому смыслу отличается от величины τ в правой части уравнения (5.9) – времени, в течение которого в некоторой фиксированной точке внутри реактора происходит изменение параметров процесса. Условно можно рассматривать
(среднее время пребывания реагентов в проточном реакторе, характеризующее для реактора вытеснения продолжительность прохождения потоком расстояния от входа в реактор до некоторой точки z на оси реактора) по физическому смыслу отличается от величины τ в правой части уравнения (5.9) – времени, в течение которого в некоторой фиксированной точке внутри реактора происходит изменение параметров процесса. Условно можно рассматривать  как некоторую «внутреннюю» характеристику реактора, непосредственно связанную с его размерами, а τ – как «внешнюю» характеристику, никак не зависящую от конструктивных особенностей реактора.
как некоторую «внутреннюю» характеристику реактора, непосредственно связанную с его размерами, а τ – как «внешнюю» характеристику, никак не зависящую от конструктивных особенностей реактора.
Говоря о среднем времени пребывания  для реактора идеального вытеснения, следует помнить, что в силу первого допущения о плоском профиле линейных скоростей действительное время пребывания всех частиц потока в аппарате будет одинаковым и как раз равным
для реактора идеального вытеснения, следует помнить, что в силу первого допущения о плоском профиле линейных скоростей действительное время пребывания всех частиц потока в аппарате будет одинаковым и как раз равным  . Однако, для единообразия в дальнейшем для всех проточных реакторов, и в том числе для реактора идеального вытеснения, будем использовать
. Однако, для единообразия в дальнейшем для всех проточных реакторов, и в том числе для реактора идеального вытеснения, будем использовать  как удобную характеристику, пропорциональную объему реактора.
как удобную характеристику, пропорциональную объему реактора.
Уравнение (5.11) для стационарного режима реактора идеального вытеснения можно проинтегрировать относительно  :
:
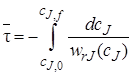 (5.12)
(5.12)
или, если J – исходный реагент,
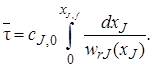 (5.13)
(5.13)
Уравнения (5.12), (5.13) по виду напоминают уравнения (5.2), (5.3) для периодического реактора идеального смешения.
Если считать, что элементарный объем dV,для которого составлялся материальный баланс, может двигаться вместе с потоком, в поршневом режиме он может рассматриваться как своеобразный периодический микрореактор идеального смешения, время проведения реакции в котором равно среднему времени пребывания реагентов в реакторе идеального вытеснения.
Уравнения (5.12) и (5.13) могут быть использованы для расчета размеров изотермического реактора идеального вытеснения и глубины протекающего в нем процесса.
Пример 5.2.Определить среднее время пребывания реагентов в проточном реакторе идеального вытеснения для условий примера 5.1 (реакция второго порядка 2А 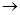 R + S, кинетическое уравнение wrA = 2,5сА2, сА0 = 4 кмоль/м3, хА,f = 0,8).
R + S, кинетическое уравнение wrA = 2,5сА2, сА0 = 4 кмоль/м3, хА,f = 0,8).
Решение. Используем для расчета уравнение (5.13):
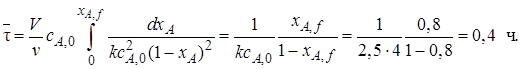
Таким образом, для достижения аналогичных результатов значения  = V/v для реактора идеального вытеснения (0,4 ч) существенно меньше, чем значение
= V/v для реактора идеального вытеснения (0,4 ч) существенно меньше, чем значение  для проточного реактора идеального смешения.
для проточного реактора идеального смешения.
Пример 5.3.Уравнения материального баланса (5.18)и (5.19)могут быть использованы не только для определения среднего времени пребывания  и размеров реакционного пространства при заданной глубине химического превращения (проектный расчет). Но и для решения обратной задачи (поверочного расчета) при заданных размерах аппарата для определения реакционного состава на выходе из него.
и размеров реакционного пространства при заданной глубине химического превращения (проектный расчет). Но и для решения обратной задачи (поверочного расчета) при заданных размерах аппарата для определения реакционного состава на выходе из него.
Приведем примеры аналитического решения математической модели (5.18) и (5.19) для некоторых частных случаев.
Простая элементарная реакция А 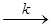 R. Скорость такой реакции wrA = kсAсB. Подставляем это кинетическое уравнение в уравнение материального баланса
R. Скорость такой реакции wrA = kсAсB. Подставляем это кинетическое уравнение в уравнение материального баланса
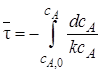
и интегрируем 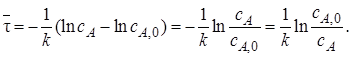
Тогда 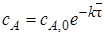
и 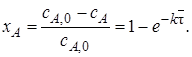
Обратимая реакция А 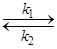 R. При условии, что cR,0 = 0,
R. При условии, что cR,0 = 0,
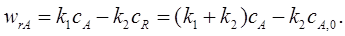
Подставим это значение wrA в формулу (5.12):
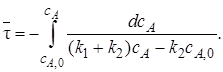
Интеграл может быть записан в таком виде:
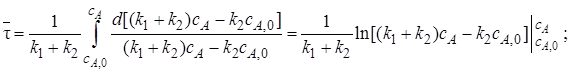
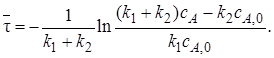
Из последнего выражения
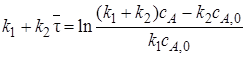
или 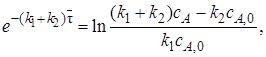
откуда 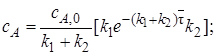
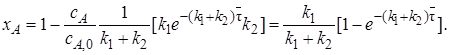
Параллельная реакция 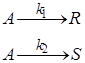 . Для этой реакции скорость по компоненту A wrA = (k1 + k2)cA и выражения для сА и хА будут:
. Для этой реакции скорость по компоненту A wrA = (k1 + k2)cA и выражения для сА и хА будут:
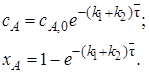
Выражение скорости по компоненту R
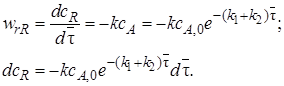
Интегрируя левую часть равенства в пределах от cR,0 до cR и правую – от нуля до  (при этом cR,0 = 0), получим
(при этом cR,0 = 0), получим
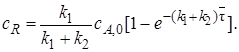
Аналогично находим 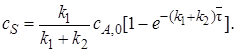
Дата добавления: 2015-06-17; просмотров: 8122;
