Равновесие химических реакций

Под воздействием подвода или отвода энергии в форме теплоты или работы происходит изменение состояния термодинамической системы (значений термодинамических параметров), называемое термодинамическим процессом. Процессы, представляющие собой непрерывный ряд равновесных состояний, называют равновесными. При этом равновесным считают состояние, в которое приходит система при постоянных внешних условиях, характеризуемое неизменностью во времени термодинамических параметров и отсутствием в системе потоков вещества и теплоты.

Устойчивое равновесие характеризуется следующими общими условиями:

1) неизменностью равновесного состояния системы во времени при постоянных внешних условиях;

2) подвижностью равновесия (самопроизвольным восстановлением состояния равновесия после снятия внешнего воздействия, вызвавшего отклонение системы от положения равновесия);

3) динамическим характером равновесия, т. е. установлением и сохранением равновесия вследствие равенства скоростей прямого и обратного процессов;

4) возможностью подхода к состоянию равновесия с двух противоположных сторон;

5) минимальным значением энергии Гиббса G в изобарно-изо­термических и энергии Гельмгольца F в изохорно-изотермических процессах (dG = 0, d²G > 0, dF = 0, d²F > 0).

Из этих общих условий выводятся конкретные условия для химического равновесия.

Химические реакции, как правило, обратимы: наряду с химическим взаимодействием между исходными веществами (прямая реакция) протекает взаимодействие и между продуктами (обратная реакция). По мере протекания процесса скорость прямой реакции уменьшается, а скорость обратной реакции увеличивается; в какой-то момент времени скорости прямой и обратной реакций становятся равными – наступает состояние химического равновесия. Химическое равновесие характеризуется неизменностью числа молекул веществ, составляющих химическую систему, при неизменных внешних условиях. Так как условием равновесия при постоянных температурах Т_ирслужит минимум энергии Гиббса (G = 0), то в условиях химического равновесия должно также соблюдаться равенство

,

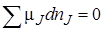гдеμ_J – химический потенциал компонента J; n_J – количество компонента J (моль).

Известно, что химическим потенциалом называется величина

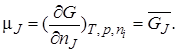
Большая положительная величина μуказывает на высокую реакционную способность частиц.

Закон действующих масс.Впервые зависимость направления химического процесса от концентрации реагирующих веществ установил Н. Н. Бекетов (1865), убедительно обосновав это положение значительным числом опытов. В математической форме закон действующих масс был выражен Гульдбергом и Вааге (1867).

Рассмотрим кинетический вывод закона действующих масс на примере гомогенной реакции

аА + bВ 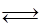rR + sS. (I)

Как известно из курса общей химии, скорость прямой реакции пропорциональна произведению концентраций реагентов А и В:

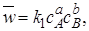
а скорость обратной реакции – произведению концентраций продуктов R и S:

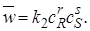
Каждая концентрация возведена в степень, равную стехиометрическому коэффициенту компонента в химическом уравнении. Из условия равенства скоростей прямой и обратной реакций в момент химического равновесия

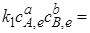
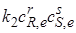
получаем

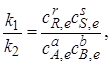
где 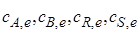– равновесные концентрации.

Отношение констант скоростей, называемое константой равновесия, обозначим через К_с. Получаем выражение закона действующих масс:

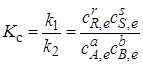.(2.1)

Как следует из выражения (2.1), константа равновесия не зависит от концентрации, так как изменение концентрации одного из участников реакции вызовет такие изменения концентрации всех остальных веществ, что К_ссохранит свое числовое значение. Таким образом, основное значение закона действующих масс состоит в том, что он устанавливает связь между равновесными концентрациями всех реагирующих веществ.

При анализе реакций, протекающих в газовой фазе, константу равновесия выражают через парциальные давления:

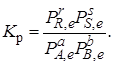
Так как в соответствии с уравнением Менделеева – Клапейрона
р_J = с_JRT,то

К_c = К_р(RT)^–∆n,

где ∆n = (r + s – a – b),если все участники реакции (I) – газообразные вещества.

Константу равновесия можно выразить также через отношение молярных долей N_J участников реакции:

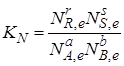
или через их количество n_J (моль):

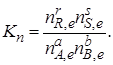
Для реальных систем константу равновесия выражают через летучести f или активности а. Так, для рассматриваемой реакции (I)

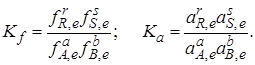
При небольших давлениях при любых температурах

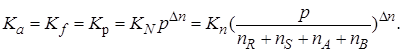(2.2)

Константа равновесия и энергия Гиббса. Уравнение изотермы Вант-Гоффа. Для рассматриваемой реакции (I) изменение энергии Гиббса выразится уравнением

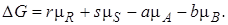(2.3)

Поскольку все участники реакции – идеальные газы, то при постоянной температуре

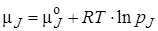, (2.4)

где 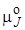– стандартный химический потенциал вещества J (индекс ° означает стандартное состояние). Для идеальных газов за стандартное принято их состояние, при давлении 0,098 МПа и температуре 298 К. Подставляя химические потенциалы, выраженные в соответствии с формулой (2.4), в уравнение (2.3) и группируя слагаемые, получим

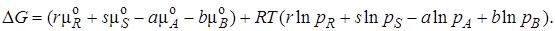
Так как первое выражение в скобках есть ∆G^o, т. е. изменение энергии Гиббса в стандартном состоянии, то

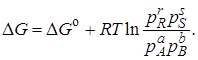
В условиях химического равновесия ∆G = 0 и, следовательно,

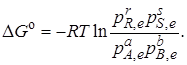
Стандартная энергия Гиббса является характерной для реакции постоянной величиной. Поэтому и выражение под знаком логарифма должно быть постоянным. Обозначив его через K_р, получим

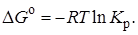(2.5)

Величина К_р,входящая в уравнение (2.5), является термодинамической константой равновесия.

Не следует забывать, что в выражение термодинамической константы равновесия входят не абсолютные значения равновесных парциальных давлений или концентраций веществ, участвующих в реакции, а относительные, т. е. безразмерные величины (например, давления, отнесенные к значениям стандартного давления). Поэтому термодинамические константы равновесия безразмерны.

Уравнение (2.5) называется уравнением изотермы Вант-Гоффа. Оно в общем виде связывает между собой энергию Гиббса и константу равновесия, которую можно вычислить, зная ∆G^o.

Значения стандартных энергий Гиббса образования многих тысяч химических соединений сведены в таблицы термодинамических свойств и приведены в справочной литературе. В случае отсутствия табличных значений ∆G^o их рассчитывают, используя уравнение

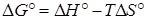, (2.6)

где ∆Н°, ∆S° – стандартные изменения энтальпии и энтропии. Значения этих стандартных термодинамических величин также приводятся в литературе.

Порядок и знак величины ∆G^o позволяют качественно предвидеть положение равновесия реакции. Если ∆G^o<<0, равновесие сдвинуто вправо, выход продукта велик, а константа равновесия имеет большое числовое значение. Если ∆G^o >> 0, равновесие сдвинуто влево, выход продукта мал, К_р<< 1.

Для протекания реакции слева направо благоприятны большие отрицательные значения ∆Н° (т. е. значительный тепловой эффект) и большие положительные значения ∆S° (возрастание энтропии). Энтропийный член входит в уравнение (2.6) в виде произведения T∆S°,поэтому и повышение температуры усиливает влияние, оказываемое изменением энтропии. В условиях равновесия при любой температуре ∆Н° = T∆S°,т. е. влияние энергетического и энтропийного факторов одинаково.

Решая совместно уравнения (2.5) и (2.6) относительно К_p,получим

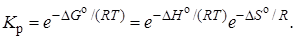(2.7)

Из анализа выражения (2.7) очевидно, что для экзотермических реакций (∆Н° < 0), протекающих с возрастанием энтропии, K_р> 1, a ∆G°<0. Для эндотермических реакций (∆Н° > 0) при убыли энтропии (∆S° < 0) самопроизвольное протекание процесса невозможно. Если ∆Н° и ∆S° имеют один и тот же знак, термодинамическая вероятность протекания процесса определяется конкретными значениями ∆Н°, ∆S° и Т.

Рассмотрим на примере реакции синтеза аммиака совместное влияние ∆Н° и ∆S° на возможность осуществления процесса (значения термодинамических функций для участников процесса указаны под уравнением реакции):

N₂ + 3Н₂ 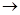2NH₃

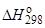0 0 2∙(–46,1)

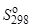191,6 3∙130,4 2∙192,4

Для данной реакции:

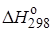= –92,2 кДж/моль, 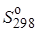= 198,0 Дж/(моль ∙ К),

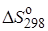= 59 кДж/моль, 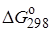= –33,2 кДж/моль.

Из приведенных данных видно, что изменение энтропии отрицательно и не благоприятствует протеканию реакции, но в то же время процесс характеризуется большим отрицательным энтальпийным эффектом 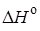,благодаря которому и возможно осуществление процесса. С ростом температуры реакция, как показывают калориметрические данные, становится еще более экзотермической (при температуре 725 К 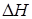= –113 кДж/моль), однако при отрицательном значении 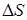повышение температуры весьма существенно уменьшает вероятность протекания процесса.

Химическое равновесие в гетерогенных реакциях.Вхимических гетерогенных системах, как и в гомогенных, условием химического равновесия является соблюдение при постоянных температуре и давлении равенств:

dG = 0; .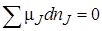

Пусть, например, в реакции (I) компонент В находится в твердом или жидком состоянии, остальные вещества – газы.

Тогда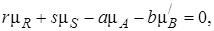

где 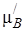, в отличие от 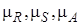, при данной температуре постоянная величина, так как является химическим потенциалом насыщенного пара компонента В.

Константу равновесия реакции (I) можно выразить через отношение парциальных давлений:

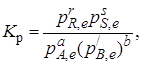
где р'_В – давление насыщенного пара компонента В, являющееся постоянной величиной.

Вводя новую постоянную величину К'_р = К_р(р'_В,е)^b,получим выражение для константы равновесия гетерогенной реакции

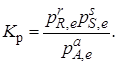
Так, например, для реакции

FeO + Н₂ = Fe + Н₂О

твердое газ твердое пар

вещ-во вещ-во

константа равновесия

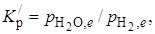
т. е. равновесие достигается при определенном (постоянном для данной температуры) отношении парциальных давлений водяного пара и водорода независимо от относительных и абсолютных количеств оксида железа и железа. Для реакции обжига известняка

СаСО₃ 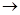СаО + СО₂

твердое твердое газ

вещ-во вещ-во

К_р = Р_СО2,е,так как в этой реакции только один газообразный участник. Равновесное давление Р_СО2,едолжно быть для каждой температуры величиной постоянной, не зависящей ни от количества карбоната кальция, ни от количества оксида кальция. Оно сильно возрастает с повышением температуры и называется давлением диссоциации.