Третье началоКТД известно как теорема Нернста [121,122], следствием которой является так называемый принцип недостижимости нуля абсолютной температуры. 13 страница
Из столбца 3 табл. 38 следует вывод о том, что линейная скорость вращения гравиполей тел, находящихся на орбитах вокруг Солнца, должна примерно на порядок превышать скорость вращения его гравиполя. И возникает вопрос: А сохраняется ли эта пропорция для спутников планет, особенно у тех из них, у которых размеры спутников имеют «солидный» разброс по величине радиуса. Рассчитаем скорости гравиполей v2 у поверхностей спутников Юпитера и занесем их в табл. 39.
|
Таблица 39
| v2 | rсп/lор | ||
| Юпитер | 1,364·108 | ||
| Амальтея | 4,073·109 | 4,420·10-4 | |
| Ио | 8,746·108 | 4,121·10-3 | |
| Европа | 9,253·108 | 2,310·10-3 | |
| Ганнимед | 7,286·108 | 2,336·10-3 | |
| Каллисто | 7,515·108 | 1,248·10-3 | |
| Атлас | 4,703·109 | 5,263·10-6 | |
| Прометей | 1,487·1010 | 5,124·10-6 | |
| Геракл | 8,139·109 | 1,709·10-6 | |
| Гефес | 1,553·1010 | 2,657·10-7 | |
| Дедал | 1,330·1010 | 3,355·10-7 | |
| Прозерпина | 1,553·1010 | 2,300·10-7 | |
| Цербер | 1,377·1010 | 2,953·10-7 |
Получается так, что линейная скорость вращения гравиполей малых спутников Юпитера приближается к скорости света, к скорости, которую электроны в естественных условиях достигают только внутри атомов и молекул либо в искусственных условиях в синхрофазотроне и, следовательно, надо ожидать, что и плотность пространства в камере синхрофазотрона соответствует плотности у поверхности этих «камешков»-спутников.
Отмечу, что интересная «случайность» (?) наблюдается в отношении приповерхностной скорости вращения гравиполя Земли v'1 = 7,91·105 см/с к аналогичной электромагнитной скорости ее же v2 = 4,562·108 см/с. Если вторую разделить на первую, то получим:
v2/v1' = 4,562·108/7,91·105 = 576.
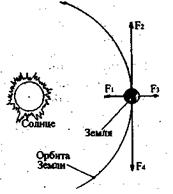
Безразмерное число 576 можно записать в виде; 576 = 4pa/3, где a ≈ a' = 137,5 > 137,04 всего на 0,3%. Если учесть, что a - постоянная тонкой структуры в квантовой механике и вспомнить, что 4pa - нижняя граница трехмерности, то это достаточно странное и вызывающее много вопросов совпадение. Но вернемся к Земле. Попробуем промоделировать качественно, как «разбегаются» волны в пространстве от пульсирующей Земли. Отметим, чтоРис. 85. длина волны, амплитуда и частота, но не фаза, от Солнца и от Земли, полученные по инварианту (2.29) длины волн l, будут иметь в либрационной точке одинаковую величину. По этому же инварианту длина волны и амплитуда от Солнца и Земли на  середине расстояния между ними тоже оказываются одинаковой величины. И чтобы Солнце и Земля не притягивали и не отталкивали друг друга, достаточно, чтобы их амплитуды совпадали по величине и фазе, но имели разный знак, т.е. силы F1 = F1' обусловленные волнами, взаимно погашались (рис. 85). Это обстоятельство и обеспечивает Земле устойчивое положение на орбите.
середине расстояния между ними тоже оказываются одинаковой величины. И чтобы Солнце и Земля не притягивали и не отталкивали друг друга, достаточно, чтобы их амплитуды совпадали по величине и фазе, но имели разный знак, т.е. силы F1 = F1' обусловленные волнами, взаимно погашались (рис. 85). Это обстоятельство и обеспечивает Земле устойчивое положение на орбите.
Волна, вызываемая самопульсацией Земли, объемна. Ее часть, идущая в сторону от Солнца (в направлении F3), будет давать Земле дополнительный импульс, «прижимая» ее к Солнцу. Такой же импульс она получает и от волн, движущихся по направлению ее движения по орбите и против этого направления. То есть с двух сторон по орбите возникают одинаковые взаимопогашающие силы F2 = F4, и, следовательно, Земля тоже должна оставаться на месте.
 Это в случае ее неподвижности относительно Солнца. В случае ее движения энергия волн самопульсации по направлению движения больше, чем поперек его. Но и в этом случае сила F1, образуемая по направлению движения, равна силе F4, направленной в противоположную сторону. А потому кажется, даже без учета сопротии-вления эфира, что планета не может двигаться за счет отталкивания от пространства. И все же она движется. Более того, образует в направлении движения впереди «себя», как уже упоминалось, бегущую ударную сфе- Рис. 86. рическую волну, «сминающую» и уплотняющую эфирное пространство перед движущимся телом и замедляя течение времени в уплотнённом пространстве. (Образуя своего рода сферическую стенку плотности.). Похоже, что это «смятое» вещественное пространство и становится основным элементом, обеспечивающим движение небесного тела в пространстве. Плотность «ударной» волны оказывается такой величины, что становится непреодолимой для набегающей на нее от тела (Земли, в частности) электромагнитной волны самопульсации. Более того, набежавшая волна этой сферической стенкой полностью отражается и с «фокусировкой» «возвращается» в сторону Земли. Отраженная волна с двойной силой воздействует на сферическое «зеркало», уплотняя «тело» последней и обеспечивая ее дальнейшее, как бы независимое от планеты, движение (рис. 86).
Это в случае ее неподвижности относительно Солнца. В случае ее движения энергия волн самопульсации по направлению движения больше, чем поперек его. Но и в этом случае сила F1, образуемая по направлению движения, равна силе F4, направленной в противоположную сторону. А потому кажется, даже без учета сопротии-вления эфира, что планета не может двигаться за счет отталкивания от пространства. И все же она движется. Более того, образует в направлении движения впереди «себя», как уже упоминалось, бегущую ударную сфе- Рис. 86. рическую волну, «сминающую» и уплотняющую эфирное пространство перед движущимся телом и замедляя течение времени в уплотнённом пространстве. (Образуя своего рода сферическую стенку плотности.). Похоже, что это «смятое» вещественное пространство и становится основным элементом, обеспечивающим движение небесного тела в пространстве. Плотность «ударной» волны оказывается такой величины, что становится непреодолимой для набегающей на нее от тела (Земли, в частности) электромагнитной волны самопульсации. Более того, набежавшая волна этой сферической стенкой полностью отражается и с «фокусировкой» «возвращается» в сторону Земли. Отраженная волна с двойной силой воздействует на сферическое «зеркало», уплотняя «тело» последней и обеспечивая ее дальнейшее, как бы независимое от планеты, движение (рис. 86).
В свою очередь отраженная космическим «зеркалом» электромагнитная волна возвращается к телу (к поверхности Земли), имея те же параметры, что и движущаяся ей навстречу волна самопульсации.
В результате на всем пространстве от «зеркала» до Земли образуются стоячие волны, обусловливающие притяжение Земли к «зеркалу» и «зеркала» к Земле. Сила F2 оказывается скомпенсированной этим притяжениеми все образование ¾ глобула вместе с планетой ¾ движется под действием сил F4 и F2 по орбите вокруг Солнца, и это движение поддерживается увеличением скорости течения времени сзади неё в области разряжения. Образуется совершенно необычная природная конструкция типа тяни-толкай, в которой компенсация одного волнового усилия обеспечивает превращение отталкивающей силы в силу толкающую. Вот почему вещественное пространство не тормозит самодвижение тел в своей среде. На рис. 86. изображена примерная схема появления эфирного «зеркала» перед движущейся планетой.
Поскольку нам неизвестны параметры сжатия и разряжения движущейся волны, а известно только изменение плотности пространства Солнечной системы, попробуем, ориентируясь на эти изменения, определить приблизительную картину взаимодействия и место возможного образования эфирного «зеркала», например, для нашей планеты. Прежде всего отметим, что зона одинаковой плотности эфирного пространства от Солнца и Земли, при положении последней в точке А, проходит по линии BE, причем ОВ = ВА. При движении планеты по орбите дуга ВСД перемещается пропорционально изменению угла ВОВ', но не пропорционально плотности пространства. Похоже, что именно эта дуга и образует сферическое эфирное «зеркало». Параметры «зеркала» определяются изменением плотности от нее до планеты. И вогнутая сфера ударной плотности должна отстоять всеми своими точками на таком расстоянии от поверхности планеты, которое обеспечивает одинаковое количественное изменение скорости и параметров волн как при движении их от планеты, так и в обратном направлении. Отмечу, что процесс движения электрических волн по направлению и против направления полета планеты по орбите в значительной степени определяется эффектом Доплера.
По-видимому, данный механизм обеспечивает движение всех тел от элементарных частиц до галактик и далее как вглубь, так и наружу, а также тел, обретающих движение в результате различных естественных или искусственных процессов. Поэтому все тела движутся в пространстве по таким траекториям, которые обусловливают им их энергетические возможности, проявляющиеся в параметрах самопульсации и энергии пространства, в котором они движутся.
На сегодня никаких параметров «зеркала» от электромагнитных волн от планет и изменения эфирной плотности пространства эмпирически не обнаружено, а теоретически их и не может быть. Однако некоторые косвенные достоверные данные свидетельствуют о существовании «зеркала». Например, об этом свидетельствуют так называемые «скачкообразные» «негравитационые» изменения кометных орбит, не имеющие естественного объяснения. Или наблюдаемое иногда как бы беспричинное деление кометного ядра. И, наконец, конфигурация ядра кометы, светящаяся часть которой достигает сотен тысяч и даже миллионов километров (какова невидимая, уплотненная ударной волной часть пространства перед головой кометы, сказать, пока ещё, невозможно).
Надо отметить еще одну возможность экспериментального обнаружения эфирного «зеркала», образующегося по орбите перед планетой. Оно, это эфирное уплотнение, является некоторым подобием гравитационной линзы, правда, достаточно слабой. И все же свет от звезд, проходящий через вогнутости «зеркала» вблизи касательной к уплотнению или через него, будет немного отклоняться от прямолинейного направления, «раздвигая» или «сдвигая» изображения звезд на фотографиях, по-видимому, в пределах 0,05-0,1%. Это, конечно, незначительные и достаточно незаметные отклонения, но все же их можно обнаружить современными фотометрическими методами. Естественно, что наибольшее отклонение может наблюдаться при прохождении лучей через эфирное «зеркало» Меркурия или Венеры, поскольку они имеют наибольшую орбитальную скорость, да и плотность эфирного пространства в районе, например, орбиты Меркурия на порядок выше, чем даже на орбите Земли или Марса (табл. 33).
7.5. Магнитные параметры планет и спин
Ранее было получена атомная структура Солнечной системы, в которой функции электронов выполняют планеты, а вокруг планет их спутники. Известно также, что электроны атомов обладают не только механическими свойствами, но и магнитными, и естественно было бы задаться вопросом: А обладают ли магнитными свойствами, например, планеты-электроны и какова зависимость между электрическими и магнитными свойствами в Солнечной системе?
Поскольку планета-электрон вращается по орбите вокруг ядра Солнца в замкнутом контуре, то в соответствии с законами электродинамики вдоль ее движения должен возникать электрический ток. Магнитные свойства замкнутого контура с током обусловливаются магнитным моментом Рт:
Pm = IS = Ipr2, (7.10)
где I = ev - сила тока, S - площадь орбитального контура. Среднюю скорость движения планеты-электрона по орбите можно представить в виде v = 2prw и, преобразовав относительно v и подставив в (7.10), получим уравнение:
Pm = evr/2, (7.11)
где Рт - называется орбитальным магнитным моментом.
Подставим в (7.10)параметры планеты Земля и получим ее орбитальный магнитный момент Рm = 1,516·1059. На рис. 87 изображена схема планеты, вращающейся вокруг Солнца против часовой стрелки, если смотреть сверху, и ее орбитальный магнитный момент, согласно электродинамике, имеет направление вниз.
Кроме электрического заряда, как показано выше, глобула-электрон обладает массой и потому при ее движении по орбите возникает механический орбитальный момент количества движения L. Он, как известно, равен:
L = mvr. (7.12)
 Подставляем числа параметров в (7.12) и получаем величину орбитального количества движения L = 1,646·1059.
Подставляем числа параметров в (7.12) и получаем величину орбитального количества движения L = 1,646·1059.
Отношение моментов Pm/L называется гиромагнитным отношением и обозначается через f. Определим его:
f = Pm/L = evr/2mvr = e/2m = 0,921.
Ровно в два раза меньше удельного заряда из таблицы 37 столбец 9. То есть можно констатировать, что гиромагнитное отноше- Рис.87. ние есть половина удельного заряда электрона глобулы Земли.
Если предположить, что Земля представляет собой электрон, движущийся в однородном магнитном поле перпендикулярно его силовым линиям, то можно определить магнитную индукцию В электрона по формуле:
F = evB. (7.13)
Поскольку сила, получаемая из (7.13), уравновешивается, как полагают, центробежной силой
F1= mv2/R, (7.14)
и F1 = F, то, приравнивая правые части (7.13), (7.14) и решая получившееся уравнение относительно магнитной индукции, находим величину В для Земли-электрона:
В = mv2/eRv= mv/el= 3,917·1025·2,989·10 /7,214·1025·l,496·1013 = 1,084·10-7.
Поскольку Земля-электрон движется в электрическом поле Солнца ЕС равном:
Ес = ec/l2 = 2,756·1026/(1,496·1013)2 = 1,231,
то можно получить силу Лорентца Fл.
Fл = еЕс + evB = 1,231·7,214·1025 + 7,214·1025·2,989·10б·1,084·10-7 =
= 8,884·1025 + 2,337·1025 = 1,122·1026.
Таким образом, оказывается, что движение планет Солнечной системы можно описывать и в терминах механики, и в терминах электродинамики, и в терминах квантовой механики. Эти возможности еще раз демонстрируют надуманность так называемых квантовых законов, искусственность и усложненность математического аппарата, описывающего несуществующие законы, закономерное появление вероятностного истолкования их и, как следствие, демонстративное отсутствие наглядности в описании квантовых явлений. Попробуем разобраться, имея весь спектр физических понятий, чем же является для модели атома ¾ Солнечной системы ¾ такое физически не представимое в квантовой механике явление, как спин электрона.
Прежде всего, отмечу, что момент импульса L описывается в квантовой механике формулой:
L = 2hÖ[l(l +1)],
где l - орбитальное квантовое число, принимающее значение l = 0, 1, 2, 3,.... (Рассмотрение состояний s, p, d, ... и т.д. опускаю за ненадобностью в настоящем изложении.)
Здесь очень важно то обстоятельство, что орбитальное число может быть равно l = 0, а, следовательно, в квантовой механике может возникнуть ситуация, когда момент импульса L отсутствует. Для структуры модели атома «Солнечная система» это равнозначно тому, что в процессе движения Земли по орбите случается ситуация, когда она со своей орбиты, да и вообще из Солнечной системы, исчезает куда-то, а затем опять появляется неизвестно откуда (не переходит с орбиты на орбиту, а как бы «испаряется» и вновь «конденсируется» в своем неизменном естестве). Это, конечно, оригинально, но вряд ли правдоподобно. Одно это обстоятельство ставит под сомнение существование орбитального квантового числа l. Тем не менее, следом за l появляется магнитное квантовое число с тем же свойством тl = 0, ± 1, ± 2, ±3, ... ±l. Причем одному значению орбитального квантового числа l (определенной величине момента импульса) соответствует 2l + 1 значений магнитного квантового числа (которое тоже может иметь величину ml = 0, с теми же последствиями). И все это великолепие квантовых чисел необходимо для того, чтобы получить различные дискретные направления вектора момента импульса, совершенно ненужные, например, в описании структуры атома Солнечной системы. Покажу, опуская вывод уравнения, это на примере сопоставления значений «постоянной» квантовой механики — магнетона Бора тб:
mб = mб = eħ/2m = f/2. (7.15)
Отмечу, что магнетон Бора µб, не может быть величиной постоянной, поскольку его КФР не равен 1: /µб = 3-1·1/3-2 = 2-1. Следовательно, количественная величина магнетона, аналогичного магнетону Бора для планет Солнечной системы, тоже не может быть постоянной. (Об этом же свидетельствует и правая часть уравнения (7.15), параметр f не может быть const.)
Мимоходом отмечу, что магнетон Бора иногда называют «атомом электричества» [158], что неудачно и способствует тер-минологической путанице. Теперь перейду к понятию «спин».
Сначала отметим, что слово «to spin» в переводе с английского означает прясть, вертеть. Его появление в квантовой механике обусловлено тем, что, объясняя некоторые эмпирические эффекты, Д. Уленбек и С. Гаудсмит приписали электрону собственные магнитный и механический моменты, представляя электрон в виде заряженной сферы определенного радиуса, вращающегося вокруг своей оси. При таком вращении сам электрон образует совокупность круговых токов и потому обладает магнитным моментом, а как протяженное тело, имеющее массу, обладает механическим моментом. То есть здесь отображается полная аналогия с вращающимся вокруг своей оси вещественным шариком. Однако очень скоро от модели вращающегося шарика пришлось отказаться по следующим обстоятельствам [148]:
• в модели отношение магнитного момента к электрическому совпадает с гиромагнитным отношением. Из опытов следовало, что гиромагнитное отношение для собственного момента в два раза больше, чем орбитальное;
• если рассматривать классический радиус электрона rе = 2,83·10-13 см (выше было показано, что эта величина никакого отношения к радиусу электрона не имеет), то при значении момента Ms = Ö3ħ/2, следующего из эксперимента, точка на поверхности электрона должна была двигаться со сверхсветовой скоростью v = 4,13·1012 см/с.
Последнее противоречило постулатуо постоянстве скорости света и стало запретном для вращения электрона с такой скоростью. Возобладал не эксперимент, а постулат.[Подчеркну, что данный постулат возобладал над здравым смыслом вообще во всей физике, ибо, как уже неоднократно отмечалось, одним утверждением постулируется одновременно с абсолютностью скорости света изотропность и невещественность пространства (его пустоту), в котором свет движется по инерции (то есть без взаимодействия, поскольку взаимодействовать не с чем) соразмерность расстояний, проходимых им в пустоте (соразмерность чему??) за единицу времени и абсолютность (??) самого времени. Более того, само логическое понятие «пустота» свидетельствует о том, что все отсутствует, что перед нами ничто, которое ничего содержать не может по определению. Т.е. качество, не имеющее отношения к физике. И появление в нем чего-то, означает изменение качества – отсутствие пустоты. К сожалению, современная физика игнорирует категорию качество.[59]. Абсолютность скорости света ¾ очень оригинальный и универсальный постулат. Переосмысливание его одного достаточно, чтобы пустить под откос всю современную теоретическую физику.]
Если же электрон увеличить до размеров планеты, то предлагаемые причины отсутствия самовращения у них отпадают сами собой, тем более, что самовращение у всех планет имеется и не только механическое, но, похоже, хотя и не видимое, электрическое v2 (табл. 38), и видимо, именно это вращение — вращение электромагнитного поля (а не точки на поверхности электрона или планеты) — отображает наличие «исковерканного» спина в квантовой механике. Посмотрим, какую величину имеет механический момент электрона-планеты при учете линейной скорости вращения электромагнитного поля у поверхности планет, например Земли и Юпитера, используя массу этих планет Мз, их радиус Rз и скорость вращения электромагнитного поля v2З (еще раз отмечу, что это электромагнитное вращение нашими приборами не фиксируется, если не считать приборами космические аппараты, и в данной работе получается в результате теоретического расчета):
MЗRЗv2З = 5,98·1027·6,371 108·4,562·108 = 1,74·1045 = ħсc.
МЮRЮv2Ю = 1,794·1027·7,13·109·1,364·108 = 1,74·1045 = ħсc,
где ħсс - постоянная Солнечной системы.
Вырисовывается совершенно необычная картина. Собствен-ный механический момент планеты-электрона оказывается равным собственному механическому моменту глобулы. Более того, он оказывается одинаковым для всех планет и для Солнца. И, следовательно, на любой орбите вокруг Солнца могут находиться только такие тела-электроны, произведение параметров М, R и v2 которых образует квант Солнечной системы ħсс. Похоже, что главное в квантовой механике не квантование орбит и других параметров (они не квантуются), а квантованная зависимость параметров тел-планет. Именно это квантование определяет всю совокупность взаимодействий между телами звездных систем и аналогичными телами в молекулах и атомах. А место на орбите «регулируется», вероятно, гиромагнитным отношением собственного магнитного момента тела планеты-электрона к ее же механическому моменту. Это отношение, скорее всего, пропорционально пульсации или вращению гравитационного или электромагнитного полей небесных тел.
Отсюда также следует, что вращение собственного электромагнитного поля планеты обусловливает существование и механического, и магнитного орбитальных моментов ее тела. И любые изменения внешнего (солнечного или галактического) гравитационного или магнитного полей, изменяющих соответствующие напряжения в глобуле планеты, будут с неизбежностью изменять направление оси вращения планеты от нескольких градусов до 180°. То есть до перемены ее географических полюсов. Такое изменение способно «выбить» из планеты «отдельные» образования (эфирогравиболиды [33]), переместив ее с одной орбиты на другую и, более того, может просто «выкинуть» планету из глобулы, как бы отправив ее подальше от Солнца в «самостоятельное» путешествие в эфирном космическом пространстве.
Зная об этом, посмотрим, какую же величину имеют собственные магнитные моменты планет-электронов?
Рт = envnrn/2. (7.16)
Уравнение (7.16) - стандартное для вычисления собственного магнитного момента элементарных частиц. Используя его, вычислим магнитный момент тел Юпитера и Земли:
PmЗ = еЗvЗ RЗ /2 = 1,542·1024·6,371·108·4,562·108 = 2,241041,
PmЮ = eЮvЮRЮ/2 = 1,537·1025·7,13·109·1,364·108 = 7,474·1042.
Проведем расчеты для остальных планет и занесем результаты в табл. 38столбец 7. Пример определения магнитного момента тел планет Земли и Юпитера показывает, что их магнитные моменты, в отличие от механических, значительно различаются, поскольку вызываются значительным расхождением величин гравитационных коэффициентов G и удельного заряда f (табл. 37, столбцы 8, 9). Отсюда становится понятным, что при рассмотрении пропорций их орбитального, механического и магнитного моментов в квантовой механике использовались несопоставимые параметры: собственный механический момент тела-электрона с магнитным орбитальным моментом его глобулы. Большой беды это не приносило, но путаницу физического понимания процесса увеличивало.
Таким образом, количественные величины магнитного и механического моментов тела планеты могут оказаться теми факторами, отношение между которыми регулирует расстояние планеты от Солнца и положение ее на орбите. Следовательно, изменение собственных параметров тела планеты, ее разрастание изнутри с изменением плотностной мерности по радиусу могут привести к выделению из трехмерного пространства планеты ее четырехмерной составляющей — эфироболида [33]. Последний, покидая Солнечную систему, вызывает изменение плотности параметров планеты и, следовательно, обусловливает «заталкивание» ее напряженностью гравиполя Солнца на более близкую орбиту. Зная уравнение (7.24), можно, применяя его к планетарным системам и в частности к Земле, рассмотреть, какие изменения могут произойти с планетой в том случае, если случится выброс большого эфирогравиболида, способного «переместить» планету на орбиту ближе к Солнцу.
7.6. О возможности планетарных излучений
Русская механика, в отличие от остальных механик, описывает природу как структурированное образование, в котором взаимосвязи всех тел и на уровне Вселенной, и на уровне макромира, и на уровне микромира строго синхронизованы (например, как синхронизованы взаимосвязи внутренних органов человеческого тела). Каждое тело занимает то положение в пространстве, которое обусловлено его параметрами и энергетическим потенциалом. Случайное (не связанное с его энергетическими возможностями) нахождение тел в том или другом месте, например Солнечной системы, исключается. Если в классической механике на любых орбитах вокруг Солнца могут находиться планеты любого размера и массы (конечно, имеющие массу на порядки меньше его), то в русской механике все тела на орбитах имеют строго пропорциональную структуру, и знание количественной величины одного параметра всех планет (например, радиуса) и массы одной планеты (например, Земли) достаточно для нахождения масс остальных планет по инварианту Rm2. Покажу это на примере Юпитера (Rю = 7,13·109 см) и Солнца (Rc = 6,97·1010 см). Находим инвариант по радиусу R3 и массе М3:
RM2 = 2,28·1064. (7.17)
Решаем инвариант относительно масс Солнца и Юпитера:
Мс = Ö(2,28 ·1064/6,96·1010) = 5,73·1026,
Mю = Ö(2,28·10б4/7,13·109) = 1,79·1027.
Масса Солнца, полученная по инварианту (7.17) равна Мс = 5,73·1026 г, а Юпитера Мю = 1,79·1027 г. И именно такие параметры имеют данные планеты в таблице 33, столбец 6.
Посмотрим, а наблюдаются ли закономерности в отношениях радиусов планет и спутников к радиусам своих орбит. То есть, верно ли предположение классической механики о случайных размерах планет и их орбит. Рассчитаем эти пропорции, и результат по планетам занесем в таблицу 38 столбец 6, по спутникам планеты Юпитера ¾ в таблицу 39, планет Сатурна, Урана и Нептуна в таблицу 40.
Прежде всего отмечу, что приведенное расстояние (промежутки между нумерованными орбитами) у каждой из планет, как и у спутников, — свои. Но у Юпитера они ограничивается 26 потенциальными орбитами, у Сатурна и Нептуна ¾ 23 и у Урана ¾ 15 орбитами (определенных по объемному коэффициенту). Если по величине этой пропорции рассматривать планеты (таблица 38 столбец 6), то у них не отмечается никаких резких переходов от одной орбиты к другой. Разница в отношениях радиусов крайних планет к радиусам своих орбит находится в пределах порядка.
При анализе же планетарных систем в отношениях радиусов спутников к радиусам орбит у всех трех планет ¾ Юпитера,
Таблица 40
| Спутники | R, км | l, тыс. км. | R/l | № орбиты |
| Сатурна | ||||
| Янус | 0,9434·10-3 | |||
| Мимас | 1,450·10-3 | |||
| Энцелад | 1,260·10-3 | |||
| Тефия | 1,695·10-3 | |||
| Диона | 1,273·10-3 | |||
| Рея | 1,233·10-3 | |||
| Титан | 1,997·10-4 | |||
| Геперион | 1,483·10-4 | |||
| Япет | 1,545·10-4 | |||
| Феба | 9,266·10-4 | |||
| Урана | ||||
| Миранда | 0,9231·10-3 | |||
| Ариель | 1,823·10-3 | |||
| Умбриэль | 9,363·10-3 | |||
| Титания | 1,141·10-3 | |||
| Оберон | 7,679·10-4 | |||
| Нептуна | ||||
| Тритон | 5,352·10-3 | |||
| Нереида | 2,157·10-5 |
Сатурна и Нептуна, имеющих по 23 потенциальной орбиты, явно имеется скачок на два порядка в системах Сатурна и Нептуна и на три порядка в системе Юпитера. Скачок показывает, что:
Дата добавления: 2015-06-17; просмотров: 538;
