Фрейми та продукційні системи

Однією з найвідоміших форм зображення знань є запропонована М.Мінським концепція фреймів. Фрейм – це опис певної стереотипної ситуації. Можуть бути фрейми-структури, фрейми-ролі, фрейми-сценарії і т.д. Кожен фрейм описує один концептуальний об’єкт, конкретні властивості якого та факти, що відносяться до нього, визначаються у слотах – структурних елементах даного фрейму. Наприклад, слотами фрейму “кімната” можуть бути “довжина”, “ширина”, “висота”, “вікна”, “двері”, “підлога” тощо. У слоти різних типів можна підставляти різні дані числа, математичні співвідношення, тексти. Тобто слоти відіграють роль, аналогічну до формальних параметрів процедури.

З кожним слотом пов’язується опис умов, за яких відбувається його означування. Слотам можна приписати певні стандартні значення, що дає змогу аналізувати за допомогою фреймів ситуації, у яких відсутнє згадування про цілий ряд деталей. Використання умовчань часто дає змогу обійтися без формального використання кванторів. Слот може мати не тільки готові значення, але й ім’я процедури, що дає змогу обчислити його значення за відомим алгоритмом, а також одну чи кілька продукцій, які описують умови та порядок його знаходження. У слоті можна розміщувати посилання на інший фрейм, що дає змогу будувати мережу фреймів та забезпечувати наслідування властивостей родових об’єктів. Такий підхід добре узгоджується з об’єктно-орієнтованою технологією. Спеціальна компонента слоту (фасет) може задавати діапазон чи список можливих значень.

Формально фрейм визначається як структура типу:

(<ім’я _ фрейму>;

<ім’я _ слоту1> (<значення _ слоту1>)

<ім’я _ слоту2> (<значення _ слоту2>)

.................................................................

<ім’я _ слотуN> (<значення _ слотуN>)

Задамо, наприклад, фрейм для об’єкту “Викладач”:

(Викладач

ПІБ (Іванов П.С.)

Вч _ ступінь (докт)

Вч _ звання (професор)

Посада (професор)

......................................)

Можна бачити аналогію з табличним поданням, поданням інформації у БД, проте можливості фреймів значно ширші.

Якщо значення слотів не визначені, то фрейм називається Фреймом-прототипом, в іншому разі – Фреймом чи екземпляром фрейму. Означування відбувається в процесі формулювання запиту чи його обробки. В описі послідовності дій використовується сценарії – скінченні множини сцен (фреймів), пов’язаних між собою умовами переходу.

Фреймові системи належать до процедуральної форми зображення знань, оскільки управління виведенням у фреймових системах реалізуються шляхом підключення складових користувачем “приєднаних” процедур. Процедури пов’язуються із слотами та класифікуються на “демони” та “слуги”. Демон активізується автоматично, коли у слот-господар підставляється певне значення чи здійснюється порівняння значень. Слуги активізується тільки за явним запитом.

З використанням приєднаних процедур можна запрограмувати будь-яку процедуру виведення на фреймові мережі. Механізм управління виведення організується наступним чином. Спочатку запускається одна з приєднаних процедур певного фрейму, який називається зразком (фрейм-прототип, у якого заповнені тільки слоти, що описують зв’язки даного фрейму з іншим). Далі шляхом пересилання повідомлень послідовно запускають приєднані процедури інших фреймів, таким чином здійснюється виведення. Фреймову модель без механізму приєднаних процедур (відповідно – без механізму пересилання повідомлень) часто використовують як базу даних системи продукцій. Інтегрована система Frame Work фірми Ashton-Tate, аналогічна за своїми можливостями Microsoft Office (текстовий редактор + СУБД + електронні таблиці + графіка), повністю реалізована у фреймі.

Фреймова модель є особливо ефективною, коли залежно від ситуації бажано застосовувати різні способи виведення. З іншого боку, у цьому випадку складнішою є оцінювання його завершеності, та існує реальна небезпека зациклювання (зависання). Фрейми є громіздкими, модифікація родо-виглядових відношень та виведення є досить трудомісткими, системи ШІ на фреймах та СМ складніші та дорожчі за логічні.

Є спеціальні мови (Genesis, FRL – Frame Representation Language) побудови експертних систем.

За умови логічного підходу твердження зображаються у вигляді формул певної логіки – звичайної, модальної, багатозначної та ін. Логічний підхід дає змогу застосувати розвинений апарат виведення нових тверджень (фактів) на основі наявних у БЗ, результат легко інтерпретується природною мовою. У цьому разі гарантується правильність виведення, а в разі його неможливості – встановлення причини ускладнення. Останню властивість використовують за підтримки несперечливості баз даних (щодо семантичних мереж забезпечити цю властивість важко).

Найчастіше використовуються продукційними системами із скінченним набором правил виведення типу:

Якщо 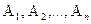то В

(Якщо виконуються всі умови від 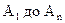, то слід виконати дію В). Частина правила після “якщо” називається посиланням, а після “то” – виведенням (дією, висновком). Антецедент (посилання) правила А являє собою зразок ситуації, коли воно повинно бути застосованим. Умови 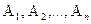як правило називають фактами. За допомогою фактів описують поточний стан предметної галузі. Факти бувають істинними, хибними або правдоподібними. В останньому випадку істинність факту припускається з певною упевненістю. Підсумкову умову можна розглядати як зразок ситуації, в якій слід виконати належну дію. Дія В водночас трактується як додання нового істинного факту до опису поточного стану процесу виведення. Правила описують причинно-наслідкові зв’язки між фактами (за необхідності – також і правилами). Маючи такий опис, його неважко ввести до ЕОМ. Для цього достатньо організувати базу фактів та базу правил і побудувати інтерпретатор бази правил, який за описом поточного стану програмного забезпечення (ПЗ) робив би висновки з цих фактів.

На такій ідеї побудовано продукційні системи (рис. 7).

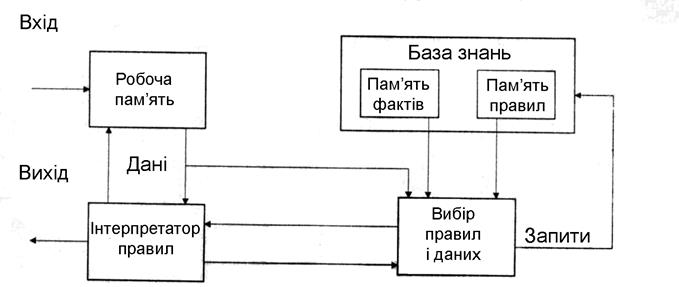
Рис. 7. Структура продукційної системи

В цих системах використовуються два основних механізми виведення: прямий та зворотний (виведення від даних та виведення від цілі відповідно). У першому випадку йдуть від відомих фактів і на кожному кроці виведення застосовують усі допустимі (з істинними посиланнями) правила, які породжують нові факти доти, поки не буде породжено факт-ціль. У другому випадку виведення йде у зворотному напрямі. Якщо ціль узгоджується з висновком правила, то посилання на правила приймають за підціль чи гіпотезу, і цей процес повторюється доти, поки не буде отримано співпадіння підцілі з відомими фактами. Чисто пряма низка веде до некерованого режиму задання питань в діалоговому порядку. Зворотна, як правило, сприятиме настійливому просуванню, але потребує попереднього визначення цілі. Найбільш вдалі системи використовують комбіновані варіанти.

У роботі з неповними (неточними) даними система має бути здатною робити припущення, а за умови отримання нової інформації, в разі потреби відмовлятися від зроблених припущень (цілей) та наступних розумових висновків. У деяких випадках можна вважати, що припущення Х має місце, якщо, використовуючи обмежені ресурси, неможливо довести протилежне.

За умови невдалого виведення на черговому кроці виконується повернення, яке легко реалізується за допомогою магазину (стеку). Проте повертатися потрібно не на один крок назад, а до точки, де було зроблено хибне припущення.

Переваги продукційних систем такі:

1) модульність – кожне правило описує невеликий, відносно незалежний фрагмент знань;

2) інкрементність – можливість додання нових правил незалежно від інших правил;

3) зручність модифікації як наслідок модульності та інкрементності;

4) прозорість системи (легкість простеження логіки та пояснювання виведення).