Закон Кулона.

Сыпучие грунты.

Сыпучие грунты при увеличении на них внешнего давления (на величину порядка нескольких бар) незначительно изменяют свою плотность и практически этими изменениями при испытании сыпучих грунтов на предельное сопротивление сдвигу можно пренебречь.

Рис. 3.10. Кривые горизонтальных перемещений образцов при разных значениях σ (а) и график сопротивления сдвигу образцов песчаного грунта (б).

После нагружения образца грунта некоторой сжимающей (вертикальной) нагрузкой прикладывают сдвигающую (горизонтальную) нагрузку, увеличивая её до тех пор, пока не возникнут без дальнейшего увеличения сдвигающей нагрузки незатухающие, прогрессивно возрастающие деформации сдвига (рис. 3.10.а) и произойдёт срез (скольжение) одной части образца грунта по другой. Величину максимального предельного сопротивления сдвигу при данной ступени нагрузки относят к единице площади поперечного сечения образца, принимая распределение сдвигающих напряжений равномерным (уравнение (3.38)). Затем идентичный образец того же грунта нагружают большим давлением и вновь определяют максимальное сопротивление сдвигу (срезу). Опыт повторяют при нескольких уплотняющих давлениях σ₁, σ₂, σ₃ и по результатам их строят диаграмму предельного сопротивления сдвигу (рис. 3.10.б).

Как показывают результаты многочисленных испытаний, диаграмма предельных сопротивлений сдвигу для сыпучих грунтов может быть принята за прямую, исходящую из начала координат и наклонённую под углом φ к оси давлений (рис 3.10.б).

Согласно диаграмме сдвига для сыпучих грунтов можно записать:

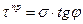, (3.39)

где tgφ - площадь поперечного сечения грунта в срезывателе;

φ - угол внутреннего трения.

Это отношение является основной прочностной зависимостью для сыпучих грунтов, установленной ещё в 1773 г. Ш. Кулоном, и может быть сформулирована следующим образом: предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трения, прямо пропорциональное нормальному давлению. Эта зависимость в механике грунтов носит название закона Кулона.

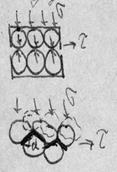
Рис. 3.11. Влияние начальной плотности сыпучего грунта на его деформации при сдвиге: а) схемы деформирования рыхлого и плотного песка; б) Кривые зависимости горизонтальной деформации песка при постоянной скорости деформирования: 1 – для плотного песка; 2 – для рыхлого песка.

Рис. 3.11. иллюстрирует влияние начальной плотности сыпучего грунта на его деформации при сдвиге при постоянной скорости деформирования. Как показывают опыты, сыпучий грунт при сдвиге достигает определённого коэффициента пористости независимо от того, имел ли он вначале плотное или рыхлое состояние. Этот коэффициент получил название коэффициента критической пористости при сдвиге для данного песчаного грунта, так как пористость плотных грунтов при сдвиге увеличивается, а более рыхлых – уменьшается.

Связные грунты.

Связные грунты отличаются от грунтов несвязных тем, что частицы и агрегаты частиц связаны между собой пластичными (водно-коллоидными) и частично жёсткими (цементационно-кристаллизационными) связями. При этом сопротивление их сдвигу будет в высокой степени зависеть от их связности (сил сцепления).

Всякое внешнее давление на водонасыщенные связные глинистые грунты при условии свободного оттока выжимаемой внешним давлением воды вызывает значительное изменение плотности-влажности, что и сказывается на общем сопротивлении грунтов сдвигу, так как прочность и количество водно-коллоидных связей пропорционально плотности-влажности глинистого грунта.

Существуют три метода испытаний:

- неконсолидированно-недренированный (быстрый) сдвиг;

- консолидированно-дренированный (медленный) сдвиг;

- консолидированно-недренированный сдвиг.

Неконсолидиронно-недренированный сдвиг – водонасыщенный грунт загружают быстро, чтобы исключить возможность его консолидации за счёт выхода воды из образца; пористые плиты в приборе заменяют сплошными, опыт выполняют за 2-3 минуты (быстрый сдвиг).

Грунт испытывают с неизменной пористостью и влажностью, так как быстро приложенная нагрузка не уплотняет его. При любом давлении сопротивление сдвигу почти не изменяется и его можно считать постоянным (рис. 3.12).

Рис. 3.12. Кривые предельных сопротивлений сдвигу связных глинистых грунтов в условиях закрытой системы (неконсолидированно-недренированных):

а) зависимость сопротивления сдвигу от влажности;

б) кривая сдвига при быстром (недренированном) срезе.

Если первая кривая (рис. 3.12.а) показывает весьма существенное влияние плотности-влажности грунта на его сопротивление сдвигу, то вторые (рис. 3.12.б) констатируют, что при быстром сдвиге τ^пр практически не зависит от величины внешнего давления, изменяясь лишь при изменении плотности-влажности грунта.

Консолидировано-дренированный сдвиг. После полной консолидации от обжимающей нагрузки очень медленно прикладывают возрастающие сдвигающие усилия, чтобы обеспечить консолидацию при сдвиге и от этой нагрузки.

При этом испытании поровое давление полностью отсутствует, так как выжидают окончания консолидации от каждой ступени загружения как нормальными, так и касательными силами.

Рис. 3.13. Кривые 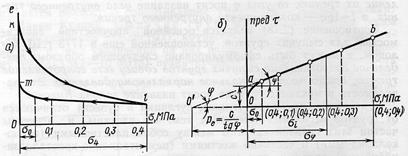предельных сопротивлений сдвигу связных глинистых грунтов в условиях открытой системы (консолидировано-дренированных): а) уплотнения (kl) и разуплотнения (lm); б) кривая сдвига.

Как показывают многочисленные испытания, кривая консолидированного сдвига связных грунтов при давлениях в диапазоне 0,05-0,5 МПа также хорошо описывается уравнением прямой линии 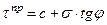, (3.40)

где с - сцепление грунта;

φ - угол внутреннего трения грунта.

Закон сопротивления сдвигу формулируется так: предельное сопротивление связных грунтов сдвигу при завершённой их консолидации есть функция первой степени от нормального давления.

Следует обратить внимание, что это уравнение получено для образцов грунта, находящихся в различном состоянии по плотности, так как перед сдвигом образцы подвергались уплотнению различным давлением. Очевидно, что при этом каждый образец будет обладать своим значением сцепления, т. е. сцепление образцов одного и того же грунта будет различным. По этой причине угол наклона прямой (рис. 3.13.б), строго говоря, не является углом внутреннего трения. Однако в механике грунтов параметр с принято называть удельным сцеплением, а φ – углом внутреннего трения.

Консолидированно-недренированный сдвиг.

Несколько образцов грунта в одинаковом начальном состоянии обжимают равными давлениями с тем, чтобы получить одну и ту же пористость, а затем быстро срезают под различными нормальными давлениями без дополнительной консолидации. Затем испытывают серию образцов, обжатых другим начальным давлением (рис. 3.14).

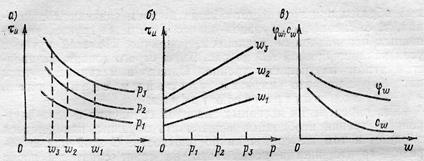Рис. 3.14. Зависимость предельного сопротивления сдвигу от влажности (а) и от давления (б); зависимость параметров φ_ω с_ω от влажности (в).

Три-четыре серии таких испытаний при различных давлениях позволяют построить семейство кривых предельного сопротивления сдвигу как функции коэффициента пористости и влажности (рис. 3.14. а).

Роль поровой воды в сопротивлении сдвигу (рис.3.15.).

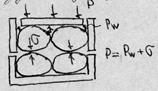
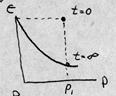
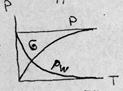
Рис. 3.15. Иллюстрация роли поровой воды в сопротивлении сдвигу.

После приложения нормальной нагрузки на водонасыщенный грунт в первый момент вся нагрузка передаётся на поровую воду. Если имеются пути для оттока поровой воды (дренированные условия), происходит отток поровой воды, падение порового давления, передача нагрузки на скелет, консолидация грунта.

Для неконсолидированного состояния полностью водонасыщенных грунтов, т. е. когда полного уплотнения от данной нагрузки ещё не достигнуто, часть сопротивления сдвигу грунта, зависящая от величины нормального давления, будет меньше, так как на скелет грунта передаётся не всё давление, а лишь эффективное σ_эфф, равное разности между полным давлением (сжимающим напряжением σ) и нейтральным u.

Тогда сопротивление сдвигу полностью водонасыщенного связного грунта при незавершённой консолидации будет по величине промежуточным между сопротивлением сдвигу, соответствующим начальной влажности грунта, и величиной, соответствующей её стабилизированному его состоянию, и определяется выражением:

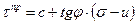, (3.41)

или 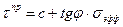(3.42)

где u - нейтральное (поровое) давление, соответствующее данной степени консолидации;

с - величина эффективного сцепления.