Определение ударного тока КЗ
Активные сопротивления определяются по отношению: 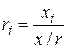 .
.
Сопротивления генераторов:
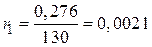 ,
, 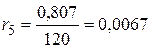 ,
, 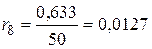 .
.
Сопротивления трансформаторов:
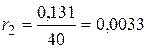 ,
, 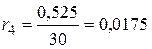 ,
, 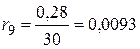 .
.
Сопротивления линий: отношение 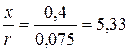 ,
,
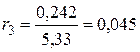 ,
, 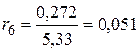 ,
, 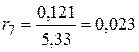 ,
, 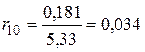 .
.
Сопротивления автотрансформатора: 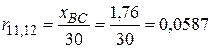 .
.
Сопротивление системы: 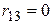 .
.
Схема замещения для активных сопротивлений составляется и преобразуется аналогично схеме замещения для реактивных сопротивлений
(рис. 4.13–4.19):
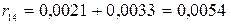 ,
, 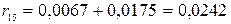 ,
,
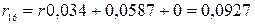 ,
, 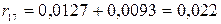 ,
,
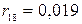 ,
, 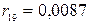 ,
, 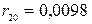 ,
, 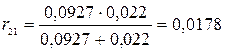 ,
, 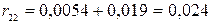 ,
, 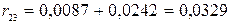 ,
, 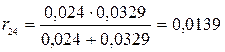 ,
, 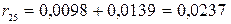 ,
, 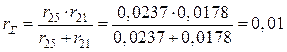 .
.
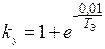 ,
,
где 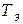 – эквивалентная постоянная времени.
– эквивалентная постоянная времени.
Если 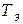 в относительных единицах, то
в относительных единицах, то
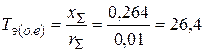 о.е.,
о.е., 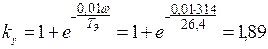 .
.
Если 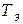 в именованных единицах, то
в именованных единицах, то
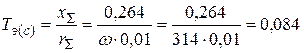 с.,
с., 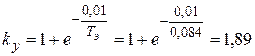 .
.
Ударный ток определяется по формуле (4.14)
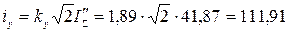 кА.
кА.
4.6.5 Определение действующего значения тока КЗ за первый период,
теплового импульса и мощности КЗ
Действующее значение тока КЗ за первый период его изменения
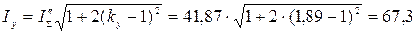 кА.
кА.
Тепловой импульс тока КЗ
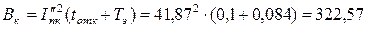
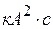 .
.
Мощность в момент времени 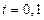 с (время отключения КЗ)
с (время отключения КЗ)
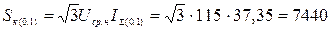 МВА.
МВА.
4.6.6 Расчет остаточных напряжений при трехфазном КЗ
Остаточное напряжение на шинах СН автотрансформатора (в точке К4):
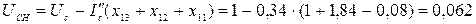
или 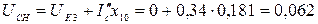 .
.
В именованных единицах: 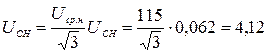 кВ.
кВ.
Остаточное напряжение в точке К5:
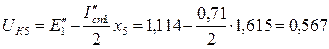 .
.
В именованных единицах: 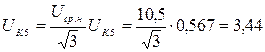 кВ.
кВ.
5 РАСЧЕТ НЕСИММЕТРИЧНОГО КОРОТКОГО ЗАМЫКАНИЯ
5.1 Общие положения
Расчет режима при несимметричном КЗ основан на использовании метода симметричных составляющих, в соответствии с которым ток и напряжение в фазах определяются как геометрическая сумма токов или напряжений прямой, обратной и нулевой последовательностей [2, 3, 7].
Учитывая, что полный ток в месте КЗ, а также токи обратной и нулевой последовательностей при несимметричном КЗ пропорциональны току прямой последовательности, основная задача расчета несимметричных КЗ будет заключаться в определении тока прямой последовательности. В свою очередь, ток прямой последовательности любого несимметричного КЗ может быть определен как ток при трехфазном КЗ в точке, удаленной от действительной точки КЗ на дополнительную реактивность 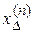 , определяемую видом КЗ.
, определяемую видом КЗ.
Если не учитывать дугу в точке КЗ (металлическое КЗ), то правило эквивалентности прямой последовательности имеет вид
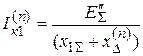 , (5.1)
, (5.1)
где 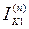 – ток прямой последовательности в точке КЗ;
– ток прямой последовательности в точке КЗ;
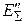 , – результирующая ЭДС схемы прямой последовательности;
, – результирующая ЭДС схемы прямой последовательности;
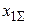 – результирующее сопротивление схемы прямой последовательности
– результирующее сопротивление схемы прямой последовательности
относительно точки КЗ;
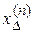 – дополнительная реактивность, определяемая видом КЗ.
– дополнительная реактивность, определяемая видом КЗ.
Для расчета несимметричных КЗ используют комплексные схемы замещения [2]. Каждый вид КЗ характеризуется соответствующей комбинацией схем замещения прямой, обратной и нулевой последовательностей и определяется соотношением симметричных составляющих токов и напряжений для особой фазы. Как отдельные симметричные составляющие, так и полные величины токов и напряжений носят комплексный характер. В выражении (5.1) и в дальнейшем для упрощения записи точки над комплексными величинами ставиться не будут.
Особой принято называть фазу, которая находится в особых условиях по отношению к двум другим фазам. За особую в расчетах всегда принимают фазу А. Все дальнейшие соотношения метода симметричных составляющих даются для фазы А.
Для расчета симметричных КЗ 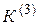 используется только схема замещения прямой последовательности. При этом, независимо от точки КЗ, она сводится к эквивалентной схеме, которая указана на рисунке 5.1.
используется только схема замещения прямой последовательности. При этом, независимо от точки КЗ, она сводится к эквивалентной схеме, которая указана на рисунке 5.1.
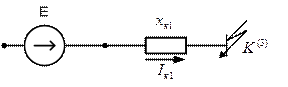
Рис. 5.1. Эквивалентная схема замещения для расчета 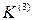
Расчет двухфазного КЗ 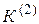 производится с помощью схем замещения прямой и обратной последовательностей. Эквивалентная схема замещения для данного случая изображена на рисунке 5.2.
производится с помощью схем замещения прямой и обратной последовательностей. Эквивалентная схема замещения для данного случая изображена на рисунке 5.2.
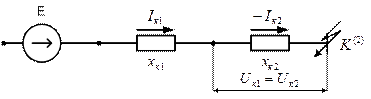
Рис. 5.2. Эквивалентная схема замещения для расчетов
двухфазного короткого замыкания
Для расчета токов и напряжений при двухфазном КЗ на землю 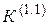 необходимо использовать схемы замещения всех трех последовательностей. Расчетная схема замещения для этого случая изображена на рисунке 5.3.
необходимо использовать схемы замещения всех трех последовательностей. Расчетная схема замещения для этого случая изображена на рисунке 5.3.
Рис. 5.3. Эквивалентная схема замещения для расчетов
двухфазного короткого замыкания на землю
Расчет токов и напряжений однофазного КЗ  в системе с заземленными нейтралями также производится с помощью схем замещения всех трех последовательностей. Расчетная схема для этого вида КЗ показана на рисунке 5.4.
в системе с заземленными нейтралями также производится с помощью схем замещения всех трех последовательностей. Расчетная схема для этого вида КЗ показана на рисунке 5.4.
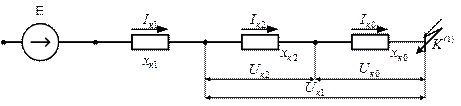
Рис. 5.4. Эквивалентная схема замещения для расчетов
однофазного короткого замыкания на землю
При расчетах всех видов несимметричных коротких замыканий, в соответствии с правилом эквивалентности прямой последовательности, достаточно определить лишь прямую последовательность тока 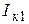 . Все остальные расчетные величины выражаются через
. Все остальные расчетные величины выражаются через 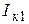 и даны в таблице 5.1.
и даны в таблице 5.1.
Для определения тока прямой последовательности требуется предварительно найти результирующие реактивности схем обратной и нулевой последовательностей и дополнительные реактивности, зависящие от вида КЗ ( 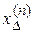 ), которые определяются по таблице 5.2.
), которые определяются по таблице 5.2.
Модуль полного тока в месте КЗ определяется как
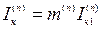 , (5.2)
, (5.2)
где 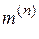 – коэффициент, зависящий от вида КЗ (табл. 5.2).
– коэффициент, зависящий от вида КЗ (табл. 5.2).
Напряжение прямой последовательности определяется по известному значению дополнительной реактивности
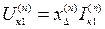 . (5.3)
. (5.3)
Напряжения отдельных последовательностей в месте КЗ определяются в соответствии с уравнениями второго закона Кирхгофа [2]:
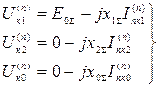 (5.4)
(5.4)
или выражаются через основные соотношения согласно таблице 5.1.
Таблица 5.1
Основные соотношения метода симметричных составляющих
| Определяемые величины | Вид короткого замыкания | |||
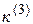
| 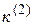
| 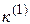
| 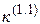
| |
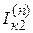
| 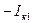
| 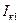
| 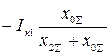
| |
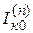
| 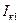
| 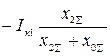
| ||
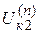
| 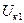
| 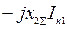 
| 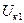
| |
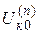
| Значение до КЗ | 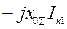
| 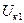
|
Таблица 5.2
Расчетные соотношения дополнительной реактивности 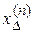
и коэффициента 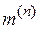 , зависящих от вида КЗ
, зависящих от вида КЗ
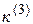
| 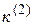
| 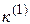
| 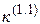
| |
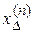
| 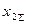
| 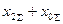
| 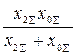
| |
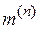
| 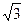
| 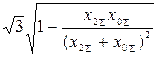
|
5.2 Определение остаточных напряжений при несимметричном КЗ
Составляющие напряжений отдельных последовательностей в заданном узле схемы можно определять суммированием (с учетом знаков) напряжений соответствующих последовательностей в месте КЗ и падений напряжений в сопротивлениях, включенных в схемах каждой последовательности между точкой КЗ и интересующим узлом 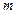 по соотношениям:
по соотношениям:
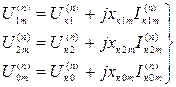 , (5.5)
, (5.5)
где 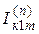 ,
, 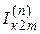 ,
, 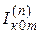 – токи соответствующих последовательностей, протекающие по сопротивлениям
– токи соответствующих последовательностей, протекающие по сопротивлениям 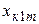 ,
, 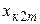 ,
, 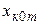 .
.
В расчетах методом эквивалентных преобразований удобнее определять напряжения отдельных последовательностей в заданной точке системы по падению напряжения на элементе.
Для определения токов 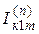 ,
, 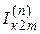 ,
, 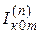 необходимо определить токораспределение в пределах схем замещения каждой последовательности. Для схемы обратной последовательности допускается применять коэффициенты распределения, найденные для схемы замещения прямой последовательности. При расчете все входящие в формулы величины должны быть выражены в одноименных единицах – относительных, либо именованных. При переводе в именованные единицы следует пользоваться соотношением
необходимо определить токораспределение в пределах схем замещения каждой последовательности. Для схемы обратной последовательности допускается применять коэффициенты распределения, найденные для схемы замещения прямой последовательности. При расчете все входящие в формулы величины должны быть выражены в одноименных единицах – относительных, либо именованных. При переводе в именованные единицы следует пользоваться соотношением
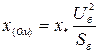 . (5.6)
. (5.6)
Остаточные напряжения определяются по отдельным последовательностям с последующим векторным суммированием для нахождения полных величин, причем по мере удаления от точки КЗ напряжение прямой последовательности увеличивается, а напряжения обратной и нулевой последовательностей уменьшаются.
Остаточное напряжение прямой, обратной и нулевой последовательностей определяется согласно рисунку 5.5 по формулам:
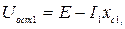 , (5.7)
, (5.7)
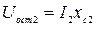 , (5.8)
, (5.8)
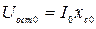 . (5.9)
. (5.9)
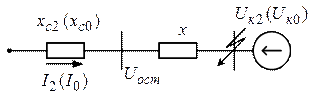
Рис. 5.5 Расчетная схема
5.3 Определение фазных величин и построение векторных диаграмм
Поскольку найденные значения определяют токи напряжения отдельных последовательностей для особой фазы, то для определения токов и напряжений в других фазах используется оператор поворота 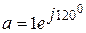 и
и 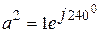 . Для токов и напряжений фаз А, В и С имеем:
. Для токов и напряжений фаз А, В и С имеем:
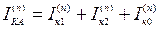
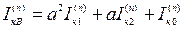
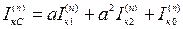 , (5.10)
, (5.10)
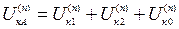 .
.
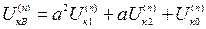
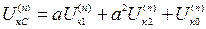
Ток, протекающий в земле при 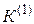 и
и 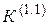 , определяется как
, определяется как
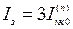 . (5.11)
. (5.11)
По полученным значениям симметричных составляющих строятся векторные диаграммы токов и напряжений как отдельных последовательностей, так и полных величин. Построение векторных диаграмм следует произвести для точки короткого замыкания. Кроме этого, строятся векторные диаграммы остаточных напряжений для заданной точки системы. При трансформации отдельных последовательностей необходимо учитывать группу соединения обмоток трансформатора [2]. Так при группе соединения звезда–треугольник–11 вектор прямой последовательности поворачивается на 30 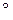 против часовой стрелки, а вектор обратной последовательности – на 30
против часовой стрелки, а вектор обратной последовательности – на 30 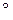 по часовой. При этом генератор воспринимает однофазное КЗ как двухфазное. Построение следует произвести в именованных единицах с указанием масштаба. Векторные диаграммы напряжений должны вписываться в треугольник линейных напряжений. Центр треугольника определяется напряжением смещения нейтрали (
по часовой. При этом генератор воспринимает однофазное КЗ как двухфазное. Построение следует произвести в именованных единицах с указанием масштаба. Векторные диаграммы напряжений должны вписываться в треугольник линейных напряжений. Центр треугольника определяется напряжением смещения нейтрали ( 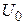 ). Фазные величины треугольника линейных напряжений в именованных единицах определяются по выражению
). Фазные величины треугольника линейных напряжений в именованных единицах определяются по выражению
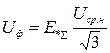 .
.
Векторные диаграммы токов и напряжений в месте КЗ представлены на рисунках 5.6, 5.7, 5.8 для различных видов несимметричных КЗ.
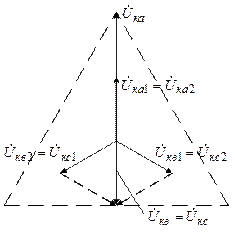
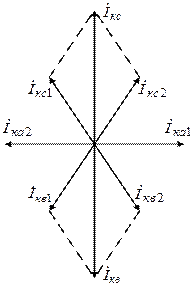
Рис. 5.6. Векторные диаграммы токов и напряжений в точке КЗ
при двухфазном коротком замыкании

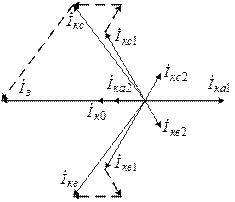
Рис. 5.7. Векторные диаграммы токов и напряжений в точке КЗ
при двухфазном коротком замыкании на землю
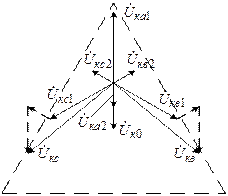
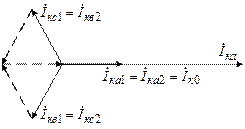
Рис. 5.8. Векторные диаграммы токов и напряжений в точке КЗ
при однофазном коротком замыкании
5.4 Особенности расчета несимметричных КЗ
методом типовых кривых
Использование метода типовых кривых для расчета несимметричных КЗ основано на правиле эквивалентности прямой последовательности. Расчет производится для прямой последовательности тока КЗ отдельно для каждого источника. Определяется аналитически начальный ток прямой последовательности отдельного источника 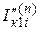 по формуле
по формуле 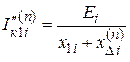 , где
, где 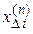 определяется по таблице 5.2.
определяется по таблице 5.2.
При этом 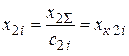 ,
, 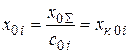 , где
, где 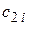 и
и 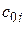 – коэффициенты распределения для схем обратной и нулевой последовательностей соответственно.
– коэффициенты распределения для схем обратной и нулевой последовательностей соответственно.
Затем определяется удаленность КЗ нахождением расчетного коэффициента 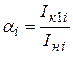 . Для полученного значения
. Для полученного значения 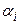 по типовым кривым определяется изменение начального значения тока прямой последовательности генератора и тока КЗ к заданному моменту времени
по типовым кривым определяется изменение начального значения тока прямой последовательности генератора и тока КЗ к заданному моменту времени 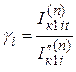 и находится необходимая величина периодической слагающей тока КЗ в момент времени
и находится необходимая величина периодической слагающей тока КЗ в момент времени 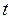 источника
источника
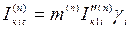 .
.
Ток от системы считается неизменным во времени и суммируется с полученными для заданного момента времени значениями тока для остальных источников
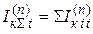 .
.
5.5 Пример расчета несимметричного КЗ в курсовой работе
Необходимо составить и преобразовать схемы замещения отдельных последовательностей и выполнить расчет несимметричных коротких замыканий.
5.5.1 Составление и преобразование схем отдельных последовательностей
Схема замещения обратной последовательности по структуре аналогична схеме замещения прямой последовательности, но не содержит ЭДС, а сопротивления элементов считаются постоянными для любого момента времени. Генераторы вводятся в схему своими сопротивлениями обратной последовательности ( 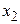 ).
).
Составляется схема замещения обратной последовательности (рис. 5.9).
Сопротивления обратной последовательности для генераторов с приведением их значения к базисным величинам:
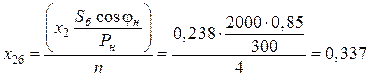 ,
, 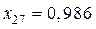 ,
, 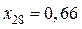 .
.
Схема замещения обратной последовательности сворачивается аналогично схеме замещения прямой последовательности.
Расчет (рис. 5.10):
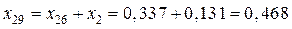 ,
, 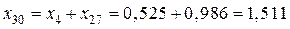 ,
,
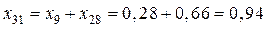 ,
, 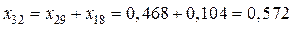 ,
,
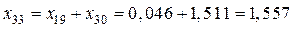 .
.
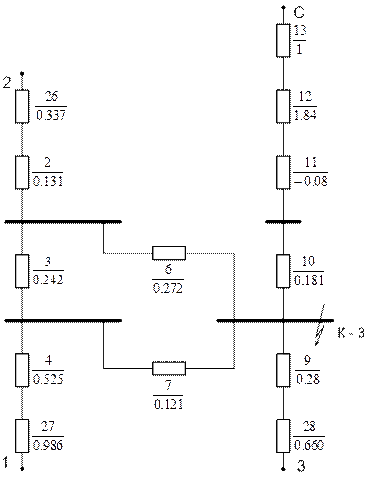
Рис. 5.9. Схема замещения обратной последовательности
Расчет (рис. 5.11):
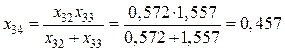 ,
, 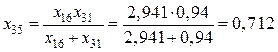 ,
,
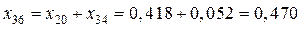 .
.
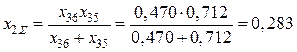 .
.
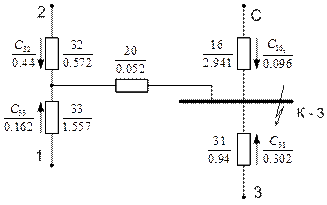
Рис. 5.10
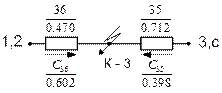
Рис. 5.11
Коэффициенты распределения от единичного тока.
Расчет (рис. 5.11):
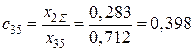 ,
, 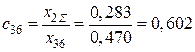 .
.
Расчет (рис. 5.10):
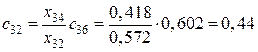 ,
, 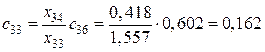 ,
,
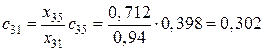 ,
, 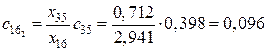 .
.
Выполняется проверка:
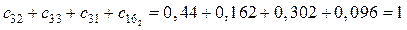 .
.
Определяются взаимные сопротивления обратной последовательности для станций и системы (рис. 5.12)
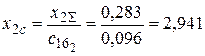 ,
, 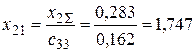 ,
,
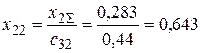 ,
, 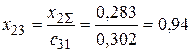 .
.
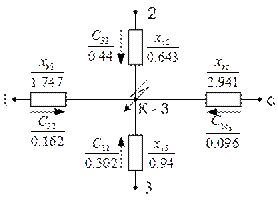
Рис. 5.12. Разделение источников схемы обратной последовательности
Схема замещения нулевой последовательности определяется участвующими в схеме трансформаторами и характером соединения их обмоток. Токи нулевой последовательности протекают через трансформаторы, нейтрали которых заземлены. Генераторы не принимают участие в схеме, т.к. оказываются отдаленными от путей протекания токов нулевой последовательности. Для автотрансформатора учитывается обмотка НН.
Составляется исходная схема замещения нулевой последовательности.
В схеме (рис. 5.13) 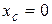 и все нейтрали заземлены.
и все нейтрали заземлены.
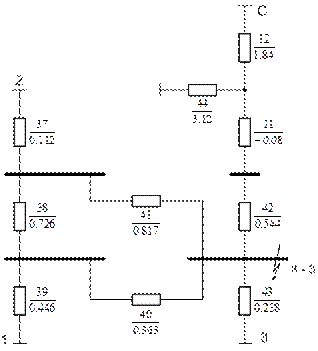
Рис. 5.13. Схема замещения нулевой последовательности
Если на станции № 1 нейтраль одного трансформатора не заземлена ( 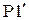 –разомкнут), то схема изменит свой вид (рис. 5.14).
–разомкнут), то схема изменит свой вид (рис. 5.14).
Определяются параметры элементов схемы замещения (рис. 5.13).
Трансформаторы:
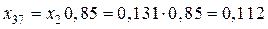 ,
, 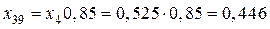 ,
,
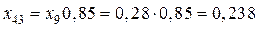 .
.
Линии:
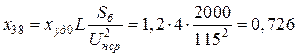 ,
, 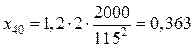 ,
,
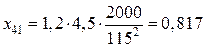 ,
, 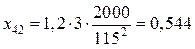 ,
,
где 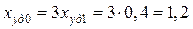 .
.
Расчет (рис. 5.15):
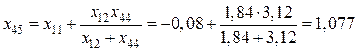 ,
,
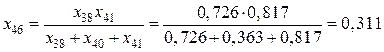 ,
,
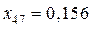 ,
,
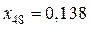 .
.
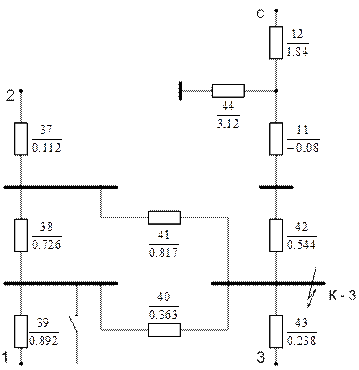
Рис. 5.14
.
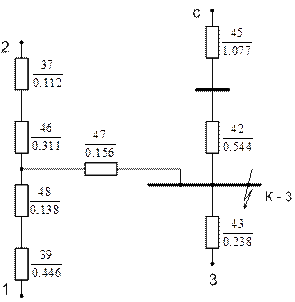
Рис. 5.15
Расчет (рис. 5.16):
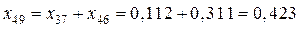 ,
,
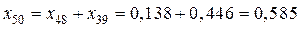 ,
,
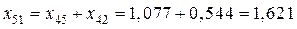 .
.
Расчет (рис. 5.17):
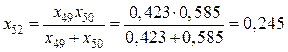 ,
, 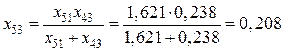 .
.
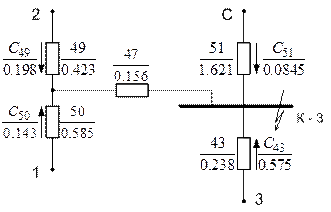
Рис. 5.16
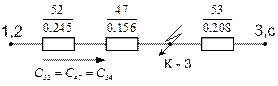
Рис. 5.17
Расчет (рис. 5.18):
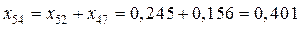 .
.
Расчет (рис. 5.19):
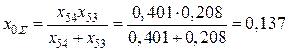 .
.
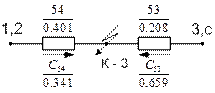

Рис. 5.18 Рис. 5.19
Коэффициенты распределения от единичного тока для нулевой последовательности
Расчет (рис. 5.18–5.16):
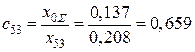 ,
, 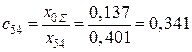 .
.
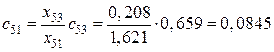 ,
, 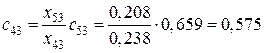 ,
,
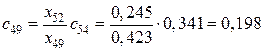 ,
, 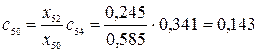 .
.
Выполняется проверка
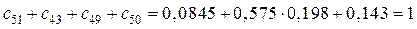 .
.
Определяются взаимные сопротивления нулевой последовательности для станций и системы (рис. 5.20):
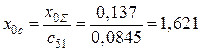 ,
, 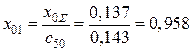 ,
,
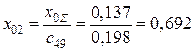 ,
, 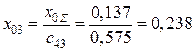 .
.
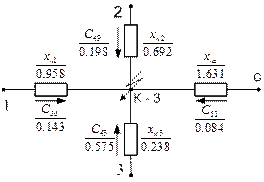
Рис. 5.20. Разделение источников для нулевой последовательности
Дата добавления: 2015-06-12; просмотров: 1509;
