Спектр и спектрограмма функции.
Слово спектр (лат. spectrum) первоначально было синонимом слова «изображение», но впоследствии спектром стали называть в оптике только цветную картинку, полученную Ньютоном в результате преломления пучка солнечного света призмой. Значительно позднее, в процессе развития учения о колебаниях и волнах, слово «спектр» приобрело в науке еще и другой смысл.
Рассмотрим функцию вида
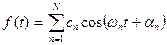 , (36-1)
, (36-1)
где 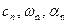 - константы.
- константы.
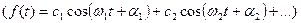
N может быть конечным или бесконечным. В первом случае функция (1) обычно называется тригонометрической суммой, во втором - тригонометрическим рядом. Мы будем называть функцию вида (1) тригонометрическим рядом, рассматривая тригонометрическую сумму как частный случай последнего.
Совокупность пар чисел (ω1, с12), (ω2, с22)…( ωn, сn2) называется спектром функции f(t). Отметим на оси абсцисс точки, соответствующие в некотором масштабе частотам ω1, ω2,…, ωN. В каждой такой точке восстановим перпендикуляр к оси абсцисс и отложим на нем отрезок, длина которого пропорциональна квадрату амплитуды (по существу интенсивности) с12, с22 , …, сN2 соответствующей синусоидальной слагаемой.
Получающуюся в результате такого построения диаграмму (рис. 36.1) мы будем называть спектрограммой функции f(t). Спектр функции - математическое понятие. Между математическим понятием спектра функции и физическим понятием спектра существует некая связь. Характер спектра


иметь в виду, что задание спектра функции f(t) не эквивалентно заданию самой функции: две функции, имеющие одинаковый спектр, могут различаться фазами компонент. Например функции ( cosωt + сos2ωt) и (cosωt + sin2ωt) имеют одинаковые спектрограммы, но различные осциллограммы.
Дата добавления: 2015-06-12; просмотров: 1049;
