Электронная теория дисперсии.
 Исследуем зависимость диэлектрической проницаемости среды от частоты ℇ(ω) световых волн, вызывающих смещение электрических зарядов вещества(а т. к. n = ℇ, то получим зависимость n(ω)). Электрическое смещение
Исследуем зависимость диэлектрической проницаемости среды от частоты ℇ(ω) световых волн, вызывающих смещение электрических зарядов вещества(а т. к. n = ℇ, то получим зависимость n(ω)). Электрическое смещение 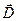 связано с напряженностью электрического поля
связано с напряженностью электрического поля 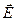
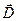 = ℇℇ
= ℇℇ 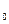
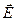 , (35-1)
, (35-1)
а с другой стороны
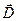 = ℇ
= ℇ 
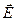 +
+ 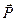 , (35-2)
, (35-2)
где 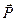 - поляризованность (см. ч.3, лекц. №18). Приравнивая (35-1) и (35-2) можно выразить ℇ. Предварительно получим выражение для поляризованности
- поляризованность (см. ч.3, лекц. №18). Приравнивая (35-1) и (35-2) можно выразить ℇ. Предварительно получим выражение для поляризованности 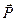 .
.
Под влиянием электрического поля электрон в атоме смещается из положения равновесия на расстояние 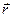 , превращая таким образом атом в электрическую систему с электрическим моментом
, превращая таким образом атом в электрическую систему с электрическим моментом 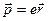 , направленную вдоль поля-диполь. (Речь идет о так называемых «оптических» электронах, слабо связанных с ядром.) Если в единице объема среды находится N атомов, то электрический момент единицы объема
, направленную вдоль поля-диполь. (Речь идет о так называемых «оптических» электронах, слабо связанных с ядром.) Если в единице объема среды находится N атомов, то электрический момент единицы объема 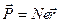 , а эта величина
, а эта величина 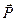 по определению является поляризованностью.
по определению является поляризованностью.
В одном атоме может быть несколько электронов, взаимодействующих с внешним полем («оптических» электронов), тогда целесообразно записать
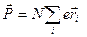 (35-3)
(35-3)
Подставляя это выражение в (35-2)
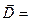 ℇ
ℇ 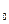
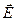
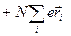 (35-4)
(35-4)
Далее определим смещение электронов 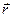 под действием внешнего периодически меняющегося поля
под действием внешнего периодически меняющегося поля  (ωt + α). При прохождении световой волны на каждый оптический электрон действует сила электрического поля волны
(ωt + α). При прохождении световой волны на каждый оптический электрон действует сила электрического поля волны
 (ωt + α) =
(ωt + α) = 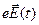 .
.
Под воздействием этой силы электроны совершают вынужденные колебания с частотой ω.
Оптические электроны согласно классическим представлениям связаны с остальной частью атома квазиупругой силой 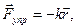 где к – коэффициент упругости, определяемый свойствами вещества,
где к – коэффициент упругости, определяемый свойствами вещества, 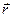 - смещение электрона из положения равновесия. Таким образом, каждый оптический электрон обладает собственной частотой колебаний ω0.
- смещение электрона из положения равновесия. Таким образом, каждый оптический электрон обладает собственной частотой колебаний ω0.
Смещение 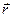 можно найти из уравнения движения (в пренебрежении затуханием колебаний)
можно найти из уравнения движения (в пренебрежении затуханием колебаний)
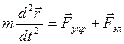 ,
,
где m – масса электрона, или
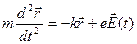 .
.
Разделим обе части на m и перенесем - 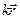 в левую часть уравнения.
в левую часть уравнения.
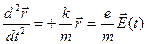
Обозначим 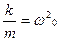 , тогда
, тогда
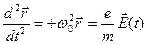
Решение этого уравнения
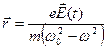
Тогда из уравнения (35-3) поляризованность
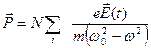
Подставляя это выражение для 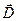 в (35-2) и приравнивая (35-2) к (35-1), получим
в (35-2) и приравнивая (35-2) к (35-1), получим
ℇℇ 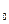
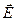 (t) = ℇ
(t) = ℇ 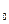
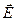 (t) +
(t) + 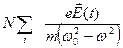
Сократим последнее равенство на 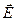 (t), разделим обе части на ℇ
(t), разделим обе части на ℇ 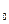 и получим выражение для диэлектрической проницаемости среды
и получим выражение для диэлектрической проницаемости среды
ℇ 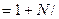 ℇ
ℇ 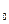
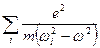 (35-5)
(35-5)
 Так, как n = ℇ, то
Так, как n = ℇ, то
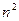
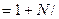 ℇ
ℇ 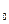
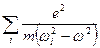 (35-6)
(35-6)


Дисперсионная кривая n(ω), соответствующая выражению (35-6) представлена на рис. 35.5 в предположении двух оптических электронов у атома. Дисперсионная кривая распадается на ряд ветвей. Вблизи ω0i (собственные частоты колебаний разных оптических электронов)  (пунктир). Если учесть реально существующее затухание колебаний, то можно получить более точное выражение для зависимости n(ω), пригодное и для областей аномальной дисперсии (где n убывает с частотой).
(пунктир). Если учесть реально существующее затухание колебаний, то можно получить более точное выражение для зависимости n(ω), пригодное и для областей аномальной дисперсии (где n убывает с частотой).
Дата добавления: 2015-06-12; просмотров: 1012;
