Разложение Фурье. Понятие о гармониках.
|
,
причем коэффициенты  (коэффициенты Фурье периодической функции) даются формулами
(коэффициенты Фурье периодической функции) даются формулами


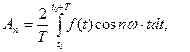
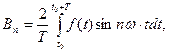
где n = 1, 2, 3,..., t0 - произвольно
(Заметим, что эта процедура называется разложением в ряд Фурье)
Синусоида с частотой ω = 2πn ¤ Т приn = 1 называется основной или первой гармоникой; соответственно при к = 2, 3… получаем вторую, третью и т. д. гармоники.
В качестве примера приведем представление прямоугольных периодических колебаний с помощью трех синусоидальных колебаний (гармоник).
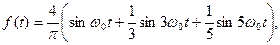
где ω0 – циклическая частота прямоугольных колебаний (ω0 = 2π¤ Т). На рис. 36.2 показаны прямоугольные колебания, первые три члена разложения и их сумма. Чем больше членов разложения, тем ближе формы суммы к форме исходных прямоугольных колебаний. Отдельные члены разложения называют еще фурье-компонентами.


Дата добавления: 2015-06-12; просмотров: 1163;

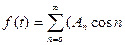 ωt
ωt 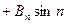 ωt)
ωt)