Число степеней свободы.
Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.
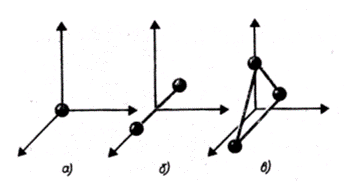
Рис. 1.1
На рис. 1.1 показаны одноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3).
Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.
Трехатомная молекула с жесткими связями имеет 6 степеней свободы: 3 - поступательного и 3 - вращательного движения (i = 6).
В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная 1/2(kT). Таким образом, средняя энергия одной молекулы равна
 (1.1)
(1.1)
1.2. Температура и ее измерение.
Температура с молекулярно-кинетической точки зрения — физическая величина, характеризующая интенсивность хаотического, теплового движения всей совокупности частиц системы и пропорциональная средней кинетической энергии поступательного движения одной частицы. Связь между кинетической энергией, массой и скоростью выражается следующей формулой:
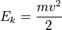 (1.2)
(1.2)
Таким образом, частицы одинаковой массы и значения скорости имеют одну и ту же температуру. C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия 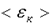 хаотического движения молекул
хаотического движения молекул 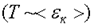 .
.
Так как энергия равномерно распределяется по степеням свободы, то связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой для идеального газа дается формулой
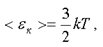 (1.3)
(1.3)
где k - постоянная Больцмана, 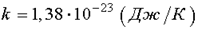 .
.
Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы. Формула (4.7) позволяет выяснить смысл абсолютного нуля: 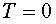 , если
, если 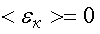 . Т. е. абсолютный нуль - это температура, при которой прекращается всякое хаотическое движение молекул.
. Т. е. абсолютный нуль - это температура, при которой прекращается всякое хаотическое движение молекул.
Давление может быть выражено через среднюю кинетическую энергию поступательного движения молекулы. Если воспользоваться формулами (1.1.) и (1.3), то получим
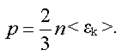 (1.4)
(1.4)
Уравнение (4.8) называется основным уравнением молекулярно-кинетической теории. Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, заключенных в единице объема.
Для измерения температуры выбирается некоторый термодинамический параметр термометрического вещества. Изменение этого параметра однозначно связывается с изменением температуры. Большинство термометров измеряют собственную температуру. Средства измерения температуры обычно проградуированы по относительным шкалам — Цельсия или Фаренгейта.
На практике для измерения температуры используют
- жидкостные и механические термометры,
- термопару,
- термосопротивление
- термометр сопротивления
- тазовый термометр
- тирометр
Жидкостные термометры основаны на принципе изменения объёма жидкости, которая залита в термометр (обычно это спирт или ртуть), при изменении температуры окружающей среды. В связи с запретом применения ртути во многих областях деятельности ведется поиск альтернативных наполнений для бытовых термометров. Например, такой заменой может стать сплав галинстан.
Механические термометры действуют по тому же принципу, что и жидкостные, но в качестве датчика обычно используется металлическая спираль или лента из биметалла.
Термометры на термопарах основаны контактной разности потенциалов – контакт между металлами с разной электроотрицательностью создаёт контактную разность потенциалов, зависящую от температуры.
Термометры сопротивления являются наиболее точными и стабильными во времени. В основе их работы лежит зависимость электрического сопротивления от температуры платиновой проволоки или платинового напыления на керамику. Температурный диапазон −200 — + 850 C.
Газовый термометр – прибор для измерения температуры, основанный на законе Шарля, который установил прямую пропорциональную зависимость между давлением газа и температурой при постоянном объеме. Наиболее точные результаты получаются, если в качестве рабочего тела использовать водород или гелий.
Пирометр – прибор для бесконтактного измерения температуры тел. Принцип действия основан на измерении мощности теплового излучения объекта измерения преимущественно в диапазонах инфракрасного излучения и видимого света. Например, позволяют визуально определять температуру нагретого тела путем сравнения его цвета с цветом эталонной нити.
1.3. Шкалы температур
Из того, что температура — это кинетическая энергия молекул, ясно, что наиболее естественно измерять её в энергетических единицах (т.е. в системе СИ в джоулях). Однако измерение температуры началось задолго до создания молекулярно-кинетической теории, поэтому практические шкалы измеряют температуру в условных единицах – градусах.
Шкала Кельвина.Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры – кельвин (К). Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры – абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию. Абсолютный ноль определён как 0 K, что равно −273.15 °C (точно). Шкала температур Кельвина, в которой начало отсчёта ведётся от абсолютного нуля.
Шкала Цельсия. В технике, медицине, метеорологии и в быту используется шкала Цельсия. В этой шкале за 0 принимают точку замерзания воды, а за 100° – точку кипения воды при нормальном атмосферном давлении. Поскольку температура замерзания и кипения воды недостаточно хорошо определена, в настоящее время шкалу Цельсия определяют через шкалу Кельвина: градус Цельсия равен кельвину, абсолютный ноль принимается за −273,15° C. Шкала Цельсия практически очень удобна, поскольку вода очень распространена на нашей планете и на ней основана наша жизнь. Ноль Цельсия – особая точка для метеорологии, поскольку связана с замерзанием атмосферной воды. Шкала предложена Андерсом Цельсием в 1742 г.
Шкала Фаренгейта. В Англии и, в особенности, в США используется шкала Фаренгейта. Ноль градусов Цельсия – это 32 градуса Фаренгейта, а градус Фаренгейта равен 5/9 градуса Цельсия. В настоящее время принято следующее определение шкалы Фаренгейта: это температурная шкала, 1 градус которой (1 F) равен 1/180 разности температур кипения воды и таяния льда при атмосферном давлении, а точка таяния льда имеет температуру +32 F. Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t°С) соотношением t°С = 5/9 (t°F - 32), 1 F = 9/5°С + 32. Предложена Г. Фаренгейтом в 1724.
Шкала Реомюра предложена в 1730 году Р.А. Реомюром, который описал изобретённый им спиртовой термометр. Во многих информационных изданиях утверждается, что шкала термометра Реомюра определялась двумя опорными точками замерзания и кипения воды. На самом деле опорная точка в первом термометре Реомюра была одна. Не стоит забывать, что первый термометр Реомюра был заполнен спиртом, температура кипения которого составляет 80 градусов по Цельсию (≈78 градусов Цельсия), что ниже температуры кипения воды. Естественно, измерить своим термометром температуру в 100 градусов по Цельсию он не мог, спирт бы кипел. Вместо этого Реомюр кратковременно опускал колбу термометра в кипящую воду и в тот момент, когда спирт закипал, отмечал его уровень на стеклянной трубке. Затем он вытаскивал термометр, ждал, пока кипение прекратится, и повторял эксперимент снова. Так образом им был найден максимальный уровень, при котором спирт начинал кипеть. Спирт при этом расширился на 8 % от своего первоначального объёма и его уровень в стеклянной трубке составил 1080 условных единиц, что соответствовало 80 градусам Реомюра. Однако, из-за того, что в качестве жидкости в те времена использовались не только спирт, но и различные его водные растворы, то многими изготовителями и пользователями термометров ошибочно считалось, что 80 градусов Реомюра это температура кипения воды. Из равенства 100 градусов Цельсия = 80 градусов Реомюра получается 1 C = 0,8°R (соответственно 1°R = 1,25 C). Хотя на самом деле на оригинальной шкале Реомюра должно быть 1°R = 0,925 C. Ещё при жизни Реомюра были проведены измерения точки кипения воды в градусах его шкалы (но не со спиртовым термометром – это было невозможно). Для точки кипения воды в градусах Реомюра получается значение 108.
Единица – градус Реомюра (°R), 1°R равен 1/80 части температурного интервала между опорными точками – температурой таяния льда (0°R) и кипения воды (80°R) 1°R = 1,25°C. В настоящее время шкала вышла из употребления, дольше всего она сохранялась во Франции, на родине автора.
1.4. Уравнение состояния идеального газа
Самой простой системой частиц является газ. В то же время его изучение имеет большое практическое значение, хотя бы потому, что газообмен определяет состояние всей биосферы Земли, в том числе человека. Вместо реального газа, между молекулами которого действуют сложные силы взаимодействия, мы будем рассматривать физическую модель - идеальный газ.
Идеальным газом называется газ, в котором собственными размерами молекул и взаимодействием между молекулами можно пренебречь. Реальные разреженные газы ведут себя подобно идеальному, так как лишь небольшая доля молекул в них находится в состоянии соударения. Например, такие газы, как воздух, кислород, азот и т. д. при комнатной температуре и атмосферном давлении по своим свойствам близки к идеальному.
Состояние заданной массы газа определяется значениями трех термодинамических параметров: давления p, объема V и температуры T. Связь между параметрами называется уравнением состояния. Уравнение состояния идеального газа может быть записано в разных формах.
В наиболее общем виде уравнение состояния идеального газа установил эмпирически французский ученый Б.П. Клапейрон и русский ученый Д.И. Менделеев. Для двух различных состояний уравнение Клапейрона имеет вид
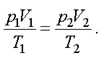 (1.5)
(1.5)
Уравнение Клапейрона-Менделеева имеет вид:
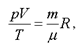 (1.6)
(1.6)
или
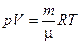 (1.7)
(1.7)
где p - давление; V - объем; T - термодинамическая или абсолютная температура (вычисляется по шкале Кельвина, которая связана с температурой по шкале Цельсия соотношением 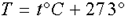 ); m - масса вещества, μ - молярная масса;
); m - масса вещества, μ - молярная масса; 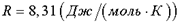 - газовая постоянная.
- газовая постоянная.
Уравнение Клапейрона - Менделеева формулируется так: произведение давления идеального газа на его объем, деленное на термодинамическую температуру, есть величина постоянная для данной массы газа.
Отношение массы вещества к молярной массе называется количеством вещества
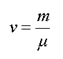 (1.8)
(1.8)
и измеряется в молях.
Уравнению (1.6) можно придать другой вид. Обозначим через m0 - массу одной молекулы, а N - полное число молекул. Тогда
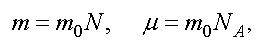
где NA - число Авогадро.
Количество вещества равно
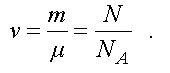 (1.8)
(1.8)
Подставим (1.8) в (1.6) и получим
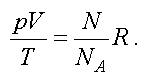
Отношение газовой постоянной к числу Авогадро есть постоянная Больцмана
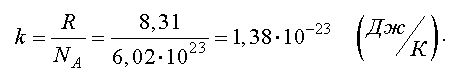
Тогда другая форма записи уравнения состояния идеального газа имеет вид
 (1.9)
(1.9)
Найдем связь давления и концентрации газа.
Концентрацией называется число молекул, заключенных в единице объема:
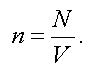 (1.10)
(1.10)
Из этого следует, что давление пропорционально концентрации, т. е.
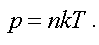 (1.11)
(1.11)
Это еще одна форма записи уравнения состояния идеального газа.
1.5. Изопроцессы. Законы Бойля-Мариотта, Гей-Люссака, Шарля.
Состояние идеального газа определяется тремя параметрами: p - давление, V - объем и T - термодинамическая температура. Изменение хотя бы одного параметра приводит к новому состоянию. Переход системы из одного состояния в другое называется процессом. Изопроцессом называется процесс, при котором один из параметров остается постоянным. Существует три изопроцесса, законы которых легко получить из уравнения (1.5).
1. Изотермический (при постоянной температуре). Это процесс описывается законом Бойля и Мариотта. Для данной массы газа при постоянной температуре произведение давление на объем газа есть величина постоянная (рис. 1.2, а).
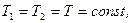
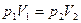 . (1.12)
. (1.12)
2. Изобарный (изобарический) – при постоянном давлении. Подчиняется закону Гей-Люссака. Для данной массы газа при постоянном давлении объем газа прямо пропорционален абсолютной температуре (рис. 1.2., б).
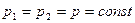
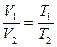 . (1.13)
. (1.13)
3. Изохорный (изохорический) – при постоянном объеме. Подчиняется закону Шарля. Для данной массы газа при постоянном объеме давление газа прямо пропорционално абсолютной температуре (рис. 1.2., в).
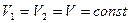
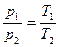 . (1.14)
. (1.14)
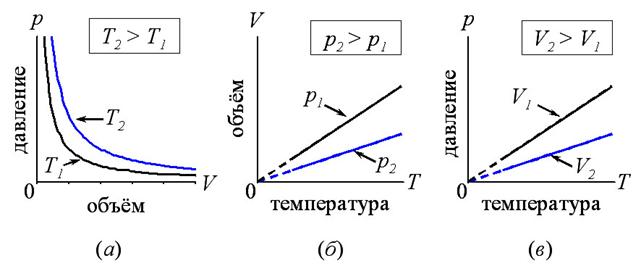
Рис. 1.2. а, б, в – изотермы, изобары и изохоры идеального газа, соответственно
Эти частные законы позволяют связать конечные параметры с начальными характеристиками.
Дата добавления: 2015-06-10; просмотров: 3217;
