Свойства распределения Максвелла.

1). При v = 0 множитель v² функции F(v) обращает ее в ноль. Это означает, что нет молекул, которые не двигались бы.

2). При v > 0 функция F(v) растет за счет множителя v². Кривая имеет максимум. Это означает, что существует определенная скорость движения молекул, такая, что вблизи нее на данный интервал dV приходится наибольшая часть молекул. Эта скорость называется наиболее вероятной V_вер.:

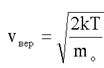(1.27)

Из распределения Максвелла вытекает, что средняя квадратичная скорость выражается

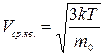(1.28)

Если учесть, что pV = RT, R = kN_A, μ = m₀N_A, а ρ = μ/V_μ, то из (12) получим другую формулу для средней квадратичной скорости – через макроскопические величины – давление p и плотность ρ:

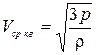(1.29)

Средняя кинетическая энергия поступательного движения одной молекулы:

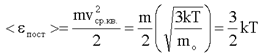(1.30)

что было получено ранее. Таким образом, средняя кинетическая энергия поступательного движения молекул определяется средней квадратичной скоростью.

Средняя арифметическая скорость движения молекул, исходя из распределения Максвелла:

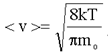(1.31)

3.) При v → ∞ кривая быстро стремится к нулю за счет экспоненциального множителя. То есть кривая не симметрична: спад кривой в одну сторону больше, чем в другую.

Как видно из формулы (1.26) и рис. 1.5 вероятность dw_v равна площади заштрихованной полоски. Ясно, что вероятность того, что молекула имеет любую скорость, равна сумме площадей всех тонких полосок и, таким образом, площади, ограниченной графиком F(v) и осью скоростей. А площадь этой фигуры не что иное, как интеграл, который, согласно условию нормировки (1.19) и соотношению(1.26), равен единице:

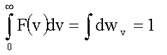(1.32)

Распределение Максвелла сильно зависит от температуры (рис. 1.6): при увеличении температуры максимум функции F(v) смещается вправо 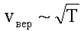и становится ниже .

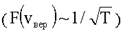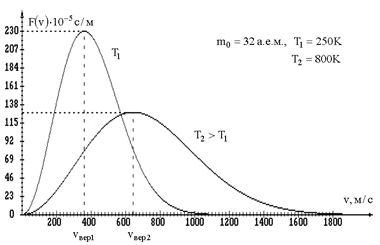
Рис. 1.6.

1.7.4. Распределение Максвелла-Больцмана.

Распределение Максвелла-Больцмана дает вероятность того, что молекула имеет определенный с точностью до dv_х, dv_y ,dv_z вектор скорости и находится, с точностью до dx, dy, dz, в определенном месте пространства:

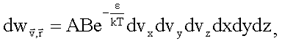(1.33)

где 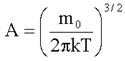; ε = ε_k + ε_n - сумма кинетической и потенциальной энергии молекулы, а 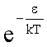- фактор Больцмана; B определен из равенства (1.22).