Распределение вихревых токов

Вихревые токи протекают непосредственно под датчиком, в небольшом объеме изделия. Их амплитуда и фаза различны в каждой точке на поверхности изделия и в глубине (рис. 4.2.1 а, б, в).

Анализ пространственной картины ВТ необходим для понимания основ метода и его эффективного практического использования. Распределение δ и ψ вихревых токов в пространстве при контроле немагнитных материалов накладными и проходными датчиками показаны на рис.4.2.1.

В каждой точке пространства рассматривается плотность ВТ и их фазу Ψ. Плоскости, в которых расположены траектории ВТ, перпендикулярны линиям напряженности возбуждающего поля. Возбуждаемые цилиндрическими датчиками ВТ протекают по окружности, соосной с датчиком. В случае контроля однородного изотропного материала значения

δ и Ψ от координаты φ не зависят.

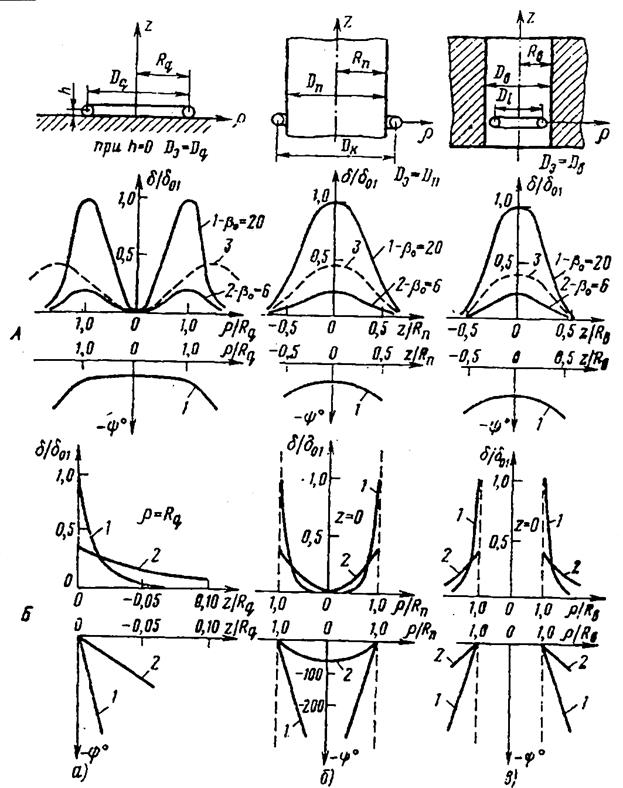
Рис. 4.2.1. Распределение плотности δ/δ₀₁ вихревых токов, возбуждаемых витком в плоском изделии (а), в прутке (б), вокруг отверстия (в): А – по поверхности; Б – по глубине; I – при высокой частоте; 2 – при низкой частоте; 3 – при наличии зазора между витком и изделием.

Распределение δ и Ψ ВТ в пространстве при контроле немагнитных материалов накладными и проходными датчиками показаны на рис.4.2.1 где

датчик заменен эквивалентным витком выражены через координаты ρ и z выражены через радиус эквивалентного контура ВТ, который равен соответственно R_q , R_п , R_в . Кривые 1 и 2 даны для различных условий возбуждения: 1 – для β_о = 20, сравнительно большой частоты или электропроводности; 2 – для β_о = 6, существенно меньших значений этих величин. Плотность ВТ выражена через максимальное ее значение на поверхности при β_о = 20.

При контроле накладным датчиком ( рис 4.2.1, а, А, δ/δ₀₁ - ρ /R_q ) на его оси δ = о. С увеличением ρ увеличивается δ, достигая максимума при ρ = R_q ,( при h = 0 ). Удаление датчика от поверхности изделия приводит к уменьшению максимума δ = ( ρ ) в случаях а, б, в, а при использовании накладного датчика – и к увеличению радиуса эквивалентного контура ВТ (кривая 3). Фазы токов, находящихся внутри эквивалентного контура, одинаковы ( рис. 4.2.1, а, А,Ψ – ρ /R_q ).

При контроле короткими проходными датчиками ( рис. 4.2.1 б, в, А,

δ/δ₀₁ – z /R) максимум δ ( z ) расположен под эквивалентным витком. Фаза ВТ изменяется вдоль оси z в обе стороны от максимума ( рис. 4.2.1, б,в, А, Ψ – z /R).

На эффекте изменения фазы ВТ вдоль координаты ρ > R_q (для накладных датчиков) или z (для коротких проходных) основаны векторно – разностные датчики. На основе постоянства фазы ВТ при о < ρ < R_q для накладного датчика основаны некоторые дифференциальные датчики.

По мере углубления в металл – увеличении z (рис 4.2.1 а, Б ), уменьшении ρ < R_q ( рис. 4.2.1, б, Б) или увеличении ρ > R_q ( рис. 4.2.1, в, Б ) - наблюдается резкое уменьшение плотности и запаздывания ВТ. В случае больших значений β_о изменение фазы ИТ по глубине носит практически линейный характер. Изменение фазы ВТ по глубине является основой многопараметрового контроля.

Анализ зависимостей δ (z, ρ, β_о ) для датчиков всех типов показывает, что на большой частоте для больших значений электропроводности в поверхностных слоях создаются ВТ большой плотности.

Из анализа графиков δ (z), δ (ρ) следует, что ВТ сосредотачиваются в том месте изделия, в котором проникающее в него поле имеет максимальное значение.

Затухание ВТ по глубине происходит по закону, близкому к экспоненциальному.

Для сравнения распределения ВТ по глубине в различных металлах при различной частоте введено понятие – условная глубина проникновения ВТ z_о. Это расстояние, измеряемое от поверхности до слоя, в котором плотность ВТ в несколько раз меньше, чем на поверхности до слоя, что соответствует уменьшению ее до 0.37.

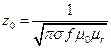
На частоте 1,5 МГц для немагнитных материалов при

σ = 0.65 · 10⁶ См/м; z_о = 0.53 мм;

σ = 10 · 10⁶ См/м; z_о = 0. 14 мм ;

σ = 25 · 10⁶ См /м; z_о = 0. 08 мм.

На частоте 150 Гц z_о увеличивается в 100 раз по сравнению с указанными значениями для тех же металлов.

Известно, что значения Z_o для некоторых металлов при различных частотах в местах дефектов сплошности материала ВТ, подтекая под дефект, могут проникать на глубину, большую чем Z_o. Поэтому изменение глубины

дефекта и в этом случае регистрируется прибором.

D_э является обобщенной переменной, учитывающей свойства материала изделия ( σ, μ ), частоту f и размеры контура ВТ, называемой обобщенным параметром β. Он характеризует процесс, происходящий внутри изделия. В случае контроля проходным датчиком D_э = D_п. или D_э = D_в (см. рис. 4.2.1. ). Поскольку для накладного датчика значение D_э зависит от расстояния эквивалентного витка возбуждающей обмотки датчика до изделия h, его вычисляют приближенно по формуле.

D_э = D_q + 1.5 h

В литературе приводятся различные выражения для β.

;

_;

_;

_.

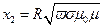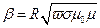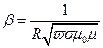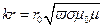Однако во всех случаях содержание их неизменно. В зарубежной литературе чаще всего обобщенный параметр представляют отношением частоты возбуждения ВТ f к так называемой граничной частоте f_g, полученной из соотношения

,

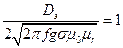если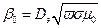

то f / f_g = β²_о / 4 , или .

При дальнейшем изложении приняты следующие обозначения для обобщенного параметра:

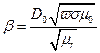- при контроле ферромагнитного материала;

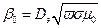- при контроле немагнитного материала.

В опубликованных ранее работах по МВТ в расчетные формулы для накладного датчика входил не диаметр эквивалентного контура ВТ, а больший средний диаметр обмоток датчика D_ср. , его вычисляют приближенно по формуле

D = D + 1,5h

В литературе приводятся различные выражения для β однако во всех случаях содержание их неизменно.

Если 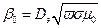- средний диаметр обмоток датчика D_ср . При расчетах на практике можно принимать D_э = D_ср , что не вносит значительных погрешностей, так как всегда стремится выполнить накладной датчик таким образом, чтобы отношение высоты его обмоток к среднему диаметру было минимальным, а в процессе контроля датчик на изделии размещают с минимальным зазором.

Полученные ранее зависимости вносимых напряжений или сопротивлений в дальнейшем приводятся без корректировки по D_э. .

Обобщенный параметр β имеет физический смысл: это отношение индуктивного сопротивления ωL_в к активному R_в эквивалентного контура ВТ в проверяемом изделии:

β =ωL_в / R_в.

Сигнал датчика представляет собой комплексную величину, состоящую в случае параметрического датчика из вносимого активного и индуктивного сопротивлений,

Z _вн = R_вн + iω t_вн,

а в случае трансформаторного датчика – активной и реактивной составляющих вносимого напряжения

U_вн = U_а.вн + i U_р.вн

Поскольку параметры ВТ (амплитуда и фаза в каждой точке траектории) зависят от электропроводности, проницаемости, сплошности материала изделия, его конструкции и положения относительно датчика, от этих же величин зависит и его сигнал. Как отмечалось, σ и μ материала входят в обобщенный параметр β. Зависимости составляющих сигнала от β_о приведены на рис. 4.2.2. Они аналогичны зависимостям магнитного потока ВТ Ф_в. и потерь мощности на ВТ Р_в в изделии от β_О.

Чаще принято рассматривать изменение сигнала датчика не по составляющим частям, а совместно на комплексной плоскости сопротивлений или напряжений. Зависимость сигнала от обобщенного параметра, положения датчика относительно изделия, его формы, размеров, сплошности материала представляет собой сложную комплексную функцию. Влияние каждого переменного на сигнал изображается графиком на комплексной плоскости R_вн, јωL_вн или U_a.вн, jU_p.вн .Значение одного из контролируемых параметров ( Д, Р, П, а также μ и σ ,выраженные через β, ) указывают непосредственно на линии графика, которую называют годографом.

С целью получения обобщенных зависимостей сигнала от параметров изделия ( свойства, размеры, форма и др.) при расчетах все размеры изделия и датчиков выражают через диаметр эквивалентного контура D_э .

Для накладного датчика, например, применяют следующие обозначения:

2h / D_э = ξ.

относительное удвоение расстояние между эквивалентным витком параметрического датчика и изделием;

h + h2 / D_э = ξ ,

– сумма относительных расстояний от эквивалентных витков возбуждающей и измерительной обмоток трансформаторного датчика до изделия;

Т / D_э = γ ,

относительная толщина листа, стенки трубы. Зазор между изделиями и эквивалентными витками проходных датчиков учитывает коэффициент заполнения η. Для проходного наружного датчика при контроле

прутка η=D²п/D²k ,

шара η = D²ш/D²k,

трубы η =D²т /D²k.

При контроле трубы проходным внутренним параметрическим или

экранным датчиком, у которого измерительная обмотка помещена в трубу, η =D²iD²в. Так же выражается η при контроле отверстий в изделиях проходным внутренним параметрическим датчиком. Обозначения абсолютных величин h , Di, D_э, Dв, Dп, Dk,Dт см. на рис. 4.2.2, и с той же целью R_вн. и ωL_вн делят на ω L_o датчика, а соответствующие вносимые напряжения – на начальное напряжение U_в на разомкнутой делят на ω L_o датчика, а соответствующие вносимые напряжения – на начальное напряжение U_в на разомкнутой измерительной обмотке датчика в свободном пространстве.

Полученные таким образом следующие величины называют нормированными или относительными:

R_вн.н = R_вн/ωL_o ; L_вн.н.=ω L_вн./ωL_о ; U_а.вн.н. =U_а.вн./U_н ;

U_р.вн.н = U_р.вн./Uн

Нормированный комплексный сигнал датчика выражается уравнениями:

Z_вн.н. = R_вн.н + j L_вн.н. = j F (β, γ )

U_вн. = U_а.вн.н. + jU_р.вн.н. = - jF (β, γ…),

а с учетом зазора между датчиком и изделием:

Rвн.н + j Lвн.н. = j F (β,γ…)е - для накладного датчика;

R + ј L = j F ( β, γ…) η-для наружного проходного датчика.

В подавляющем большинстве случаев основной при анализе этих зависимостей является годограф сигнала F(β_о) витка, плотно прижатого к немагнитному изделию (рис.4.2.2). Годографы сигналов накладных и проходных датчиков при изменении параметра β₀ и зазоров между датчиком и изделием измерительной обмотке датчика в свободном пространстве [39].

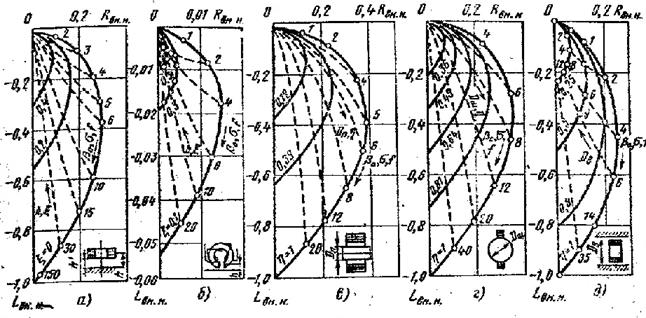
Рис.4.2.2. Годографы сигналов накладных и проходных датчиков при изменении параметра β₀ и зазоров между датчиком и изделием

1 Ф¹¹в₁

Ф¹в₁

2 1

• + • +

+ • + •

2

Ф¹в₂ Ф ¹¹ в₂

а) б)

Рис. 4.2.3. Схема контроля в отраженном (а ) и проходящем ( б ) поле

Сигнал для каждого значения β_о является максимальным; c увеличением зазора между витком и изделием сигнал уменьшается. Этот годограф отражает влияние на датчик электропроводности материала и частоты возбуждения. Причем влияние этих величин на сигнал одинаково, что следует из выражения обобщенного параметра. Как видно на рис 4.2.2 годограф, при увеличении частоты или электропроводности до бесконечности

( т.е β_о→ ∞)L_вн.н. → -1, R_вн.н. →0.

Анализируя годографы, выбирают оптимальную рабочую частоту, конструкцию датчика, измерительную схему и приемы контроля, обеспечивающие достаточную чувствительность прибора к проверяемому параметру и полное или частичное снятие влияния изменений неконтролируемых свойств изделия.

Основное влияние на вид годографа оказывает та часть ВТ, которая протекает в слоях, ближе всего расположенных к измерительной обмотке 2 датчика (рис.4.2.3). Фазы ВТ вблизи обмотки 2 в случаях а и б при контроле одного и того же изделия на одной и той же частоте могут отличаться более чем на 180°. Поэтому годографы F( σ, μ, f, T…) для двух групп классических датчиков - отраженного поля и проходящего поля (экранных) различаются существенно. В пределах каждой группы для всех типов датчиков годографы

F ( σ ), близки по форме. То же наблюдается для других годографов: F(µ), F (T) и т. д. Некоторая количественная разница между годографами для накладных, щелевых, наружных и внутренних проходных датчиков (рис.4.2.3) обьясняется тем , что та часть поля, в которую изделие помещается для контроля, у этих датчиков не одинакова.