Класификация Ферстера различных случаев миграции энергии.

Рассматривая миграцию энергии в общем случае Ферстер установил, что существуют три случая миграции, определяемые энергией взаимодействия между молекулами, между которыми имеет место миграция. Различают сильное, среднее и слабое взаимодейсивия. Энергии диполь-дипольного взаимодейсивия Eвз классифицируются посредством сравнения с энергиями ΔE и ΔE΄, характеризующими полосы поглощения и излучения молекул. Смысл этих энергий можно показать на модели конфигурационных кривых. (рис. 13)

Энергия ΔE соответствует ширине полосы поглощения или излучения (или стоксовому сдвигу), выраженной в энергетических единицах. Обычно ΔE≈3000 см‑1 для ароматических молекул. Такой же порядок величины имеет колебательный квант (1000 см-1).

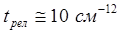Согласно значениям энергии взаимодействия Eвз, котораяа зависит от межмолекулярного расстояния и мультипольности взаимодействия, можно различить три случая:

а) сильное взаимодействие;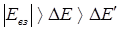

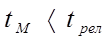
б) среднее взаимодействие;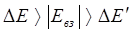

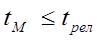
в) слабое взаимодействие;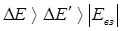

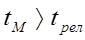
Такая классификация была предложена впервые Франком и Теллером в 1938 году.

Случай (а) описывает рассеяние экситонов, а случаи (б) и (в) касаются рассеяния и поглощения фотонов. Случай (а) рассматривается также в теории экситонов в молекулярных кристалах. А.С. Давыдова. Случай (в) – это ранее рассмотренный классический случай ферстеровской миграции.

Рассмотрим согласно Ферстеру константы скорости миграции (вероятности переноса возбуждения за 1 с.) или характерные времена переходов tМ для каждого из трёх случаев.

А) Сильное взаимодействие. При этом взаимодействии между состояниями М*М′ и М М′* столь велико, что все вибронные подурони первой молекулы находятся в резонансе с уровнями другой. В этом случае описывают состояние системы следующей зависящей от времени волновой функцией:

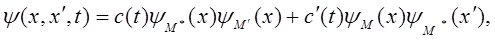
где

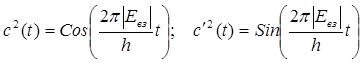
В такой системе имеют место осцилляции возбуждения в характеным временем

.

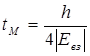Тогда

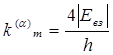(5.24)

В случае диполь-дипольного взаимодействия .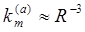

Б) Среднее взаимодействие. В этом случае механизм переноса становится другим: после возбуждения ядра атомов донора совершают неколько колебаний около положения равновесия прежде чем произойдёт акт миграции энергии. Поскольку энергия взаимодействия меньше разности колебательных уровней, то резонанс имеет место тлько между индивидуальными вибронами обоих молекул, т.е. между состояниям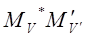и и 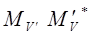, где буквы V и V' обозначают колебательные квантовые числа. Скорость переноса возбуждения вычисляется аналогично случаю а, только, при этом надо учитывать взаимодействие между вибронными собственными функциями.

В этом случае имеем

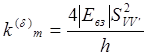(5.25)

где SVV' — интеграл перекрывания колебательных волновых функций (V – возбуждённая, а V' – невозбуждённая молекулы).

Для этих величин справедливы соотношения:

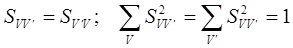
Есл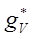и и 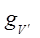— факторы заселённости соответствующих колебательных уровней, то мы имеем более общую формулу для константы миграции в этом случае:

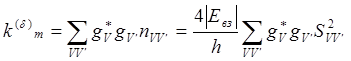(5.25а)

Величины 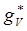и 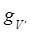удовлетворяют соотношениям 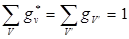из чего следует, что .

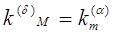В) Слабое взаимодействие. В этом случае происходит безизлучательный переходы между двумя состояниями с непрерывной энергией; при этом мы имеем для константы скорости миграции:

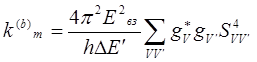(5.26)

Описанная в этом разделе теория в настоящее время применяется при интерпритации экспериментальных данных по миграции энергии по фотосинтетическим пигментам.