Индуктивно резонансный механизм; вывод формулы Ферстера; условия миграции.

Мы уже встречались с миграцией энергии, когда обсуждали изменение квантового выхода флуоресценции при тушении. Рассмотрим теперь механизмы миграции более подробно.

Миграцией энергии условились называть процессы передачи энергии от одной молекулы к другой, при которых не происходит излучение и поглощение, т.е. при миграции не успевает образоваться волновой пакет, соответствующий кванту света. Это значит, что процесс миграции происходит на расстояниях между донором и акцептором, много меньших длины волны передаваемого излучения. (RDA<<l).

В 1948 году Ферстер впервые рассмотрел индуктивно-резонансный перенос энергии возбуждения между молекулами донора и акцептора. Такой перенос определяется диполь-дипольным взаимодействием донора (Д) и акцептора (А). Этот безизлучательный перенос энергии является необратимым, идет всегда от донора к акцептору и происходит за времена, большие, чем время колебательной реакции в молекуле донора.

Тогда элементарная вероятность переноса по теории возмущений для переходов в квазинепрерывном спектре равна:

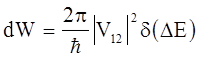(5.1)

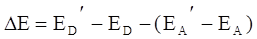(5.2)

Волновые функции начального и конечного состояний имеют вид:

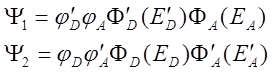(5.3)

где φ — электронные, а Φ — колебательные функции донора и акцептора.

Входящий в (5.1) матричный элемент определяется так

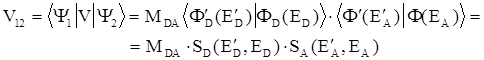(5.4)

В этом выражении SD ; SA — интегралы перекрытия колебательных волновых функций; MDA — матричный элемент диполь-дипольного взаимодействия

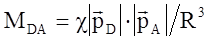(5.5)

где 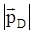, 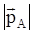— матричные элементы дипольных моментов переходов; c — фактор ориентации, выражение для которого будет приведено ниже.

Наличие d — функции требует условия

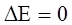, т.е.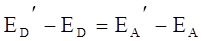

Введем распределения по энергиям для D и A в соответствующих состояниях. Пусть молекула D имеет в возбужденном состоянии распределение по энергии 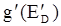, а молекула A в нижнем состоянии - распределение .

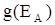Тогда полная вероятность перехода будет равна

;

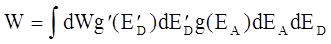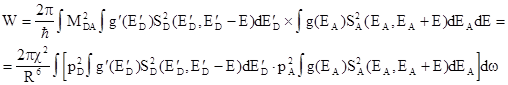(5.6)

Учтем, что dE=ħdw и введем форму линии поглощения и излучения, т.е.

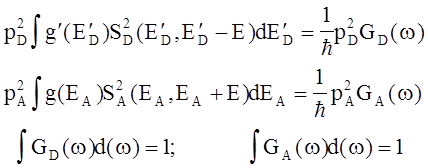
Тогда нормированный спектр излучения флуоресценции F(w) ( 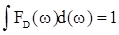) и показателя поглощения mA(w) в см‑1 связаны с формой линии следующим образом

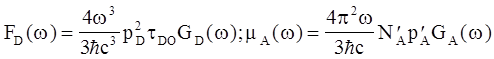(5.7)

В (5.7) — число акцепторов в 1 см3 , m определяется выражением:

I(z)=I0e-mz

Учитывая соотношение (5.7) выражение (5.6) для нормированного спектра излучения флуоресценции принимает окончательный вид:

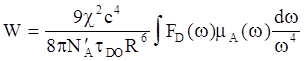(5.8)

В этой формуле c так называемый фактор ориентации, характеризующий расположение переходных дипольных моментов молекул донора и акцептора. Он имеет следующий вид:

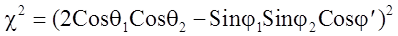
Углы φ1, φ2 — это углы между дипольными моментами переходов донора и акцептора и вектором 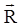, соединяющим центры молекул D и A соответственно. Угол φ΄ — это разность азимутальных углов дипольных переходных моментов и относительно вектора 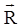. Фактор ориентации c2 можно выразить и в другом виде:

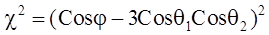
Здесь q1 и q2 углы дипольных моментов с вектором 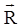, а j — это их угол между собой. Эта формула для c2 непосредственно следует из выражения для энергии диполь-дипольного взаимодействия.

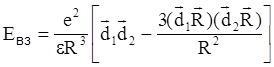
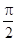
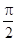Величина c2 изменяется от нуля (q1= , q2= ; j= 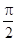дипольные моменты D и A перпендикулярны друг другу) до 4 (q1=q2=0; направления дипольных моментов совпадают с ).

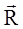Для случайной неподвижной ориентации дипольных моментов переходов в D и A c2=0,56 ,для случайного быстрого вращения c2= .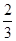

Формула (5.8) справедлива в случае, если молекулы донора и акцептора находятся в вакууме. При учете диэлектрических свойств среды формула приобретает вид:

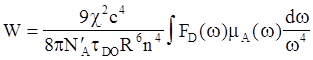(5.9)

При переходе к волновым числам 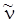, числу Авогадро NA и молярному коэффициенту экстинкции e с учетом известных соотношений

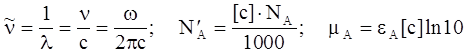
можно получить формулу (5.9) в несколько ином виде:

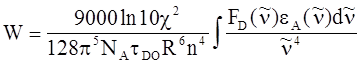(5.9a)

Учитывая, что радиационное время жизни 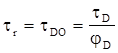и вводя 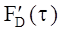- ненормированную интенсивность флуоресценции, можно получить формулу (5.9) в виде:

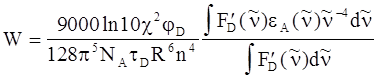(5.9б)

или в терминах длин волн мы имеем:

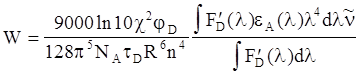(5.9в)

Таким образом, условием безизлучательной миграции является перекрывание спектров флуоресценции донора и спектра поглощения акцептора. В результате миграции энергии квантовый выход флуоресценции донора j и время жизни донора t уменьшается, поскольку появляется дополнительный канал уменьшения заселенности возбужденного состояния донора с константой миграции km=W. В свою очередь акцептор энергии может либо испускать флуоресценцию, тогда наблюдается сенсибилизированная флуоресценция, либо быть тушителем (сенсибилизированное тушение).

Каждая пара D и A в смысле миграции энергии характеризуется ферстеровским радиусом миграции R0,при котором константа скорости миграции становится равной сумме констант скоростей остальных процессов. Для определения R0 рассмотрим формулу (5.9). В ней величины jD и tD — выход и длительность флуоресценции донора в отсутствии акцептора имеют следующий вид:

(5.10)

В случае миграции энергии

(5.11)

где km=W и определяется формулами (5.9).

По определению R0 мы имеем:

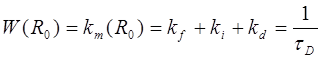(5.12)

Подставляя (5.12) в (5.9б), получим:

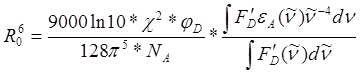(5.13)

Из соотношений (5.13) и (5.9б) следует, что

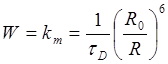(5.14)

Соотношения (5.11), т.е выход и длительность флуоресценции при наличии миграции, можно переписать в следующем виде:

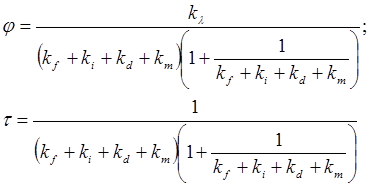(5.15)

Из (5.15) с учётом (5.10) получим на расстоянии равном радиусу Фёрстера, следующие соотношения:

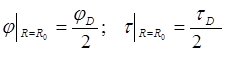(5.16)

Рассмотрим теперь выход миграции энергии p:

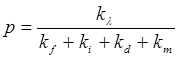(5.17)

С помощью соотношений (5.10) и (5.14) получим:

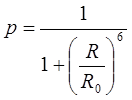(5.18)

Как видно из (5.18), выход миграции p изменяется очень резко в зависимости от расстояния. Можно выбрать выход флуоресценции φ
и длительность флуоресценции донора τ при учёте миграции энергии p. Из соотношений (5.10), (5.11) и (5.17) имеем:

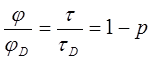(5.19)

Определяя экспериментально величину p из соотношения (5.19), можно в принципе определить расстояние между D и A, по формуле (5.18). Иногда в экспериментев место относительного уменьшения квантового выхода (или интесивности флуоресценции донора 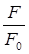) измеряют относительное тушение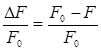

Где?