ЕЛЕМЕНТИ СТРУКТУРНОЇ КРИСТАЛЛОГРФІЇ
Мета заняття: ознайомитися з основними типами структур в кристалах та визначити їх кристалохімічні параметри.
ТЕОРЕТИЧНА ЧАСТИНА
Характерне для кристалів трьохмірне періодичне розташування матеріальних частинок можливо наочно зобразити просторовою граткою. Просторова гратка - абстрактний математичний образ, який дозволяє фіксувати розташування матеріальних частинок у просторі.
Просторову гратку кристала слід розглядати як математичну абстракцію, за допомогою якої можливо зручно (математично) описати періодичність кристалічної структури. Гратка відображає симетрію структури, незалежно від того, чи співпадає вузол з атомом того чи іншого типу чи є проміжком між атомами, Поняття «гратка кристала» неприпустимо плутати з поняттям «структура кристала».
В кожній кристалічній гратці із безкінечного числа паралелепіпедів повторюваності завжди можливо обрати такий, за допомогою якого можливо охарактеризувати всю гратку в цілому. Як було розглянуто раніше, паралелепіпед повторюваності характеризується шістьма параметрами – трансляціями 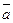 ,
,  ,
,  , які є ребрами решітки, та кутами між ними
, які є ребрами решітки, та кутами між ними  У залежності від розмірів та взаємної орієнтації цих параметрів просторові гратки мають різну симетрію, яка обмежує кількість можливих граток. Усі кристалічні гратки описуються 14 трансляційними групами, які відповідають граткам Браве, що відрізняються за формою елементарних комірок і за симетрією та поділяються на 7 кристалографічних сингоній які в свою чергу об’єднуються в 3 категорії (табл.. 3.1).
У залежності від розмірів та взаємної орієнтації цих параметрів просторові гратки мають різну симетрію, яка обмежує кількість можливих граток. Усі кристалічні гратки описуються 14 трансляційними групами, які відповідають граткам Браве, що відрізняються за формою елементарних комірок і за симетрією та поділяються на 7 кристалографічних сингоній які в свою чергу об’єднуються в 3 категорії (табл.. 3.1).
Таким чином граткою Браве називається група трансляцій, яка характеризує розташування матеріальних частинок у просторі.
Розрізняють наступні типи граток Браве (рис.3.1):
- примітивні матеріальні частинки розташовуються тільки у вузлах гратки (у вершинах елементарних паралелепіпедів).
- не примітивні – частинки розташовуються як у вузлах гратки, так і або у центрі двох протилежних граней (базоцентрована), або у центрі гратки (об’ємноцентрована), або у центрі кожної грані (гранецентрована).
- Складна (гексагональна сингонія) – складається з трьох примітивних комірок, що являють с призму з ребром паралельним собою вісі 6 порядку.
Таблиця 3.3 - Характеристика сингоній
| Категорія | Сингонія | Метрика кристалів | Головні напря- мки | Кількість класів у сингонії | Типові представ- ники | Розподіл вивчених кристалів |
| нижча | триклинна | 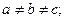 
| - | 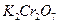
| 290– 3,5% | |
| моноклінна | 
| 
| 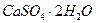
| 2345 – 27% | ||
| ромбічна | 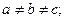 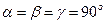
| 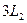
| 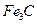
| 1980 – 23,5% | ||
| середня | тригональна | 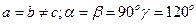
|  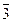
| 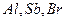
| 967 – 11% | |
| тетрагональна |  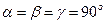
|  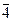
|  
| 799 – 9% | ||
| гексагональна | 
| 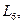 
| 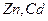
| 645 – 6% | ||
| вища | кубічна |  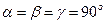
| 
| 
| 1763 20% |
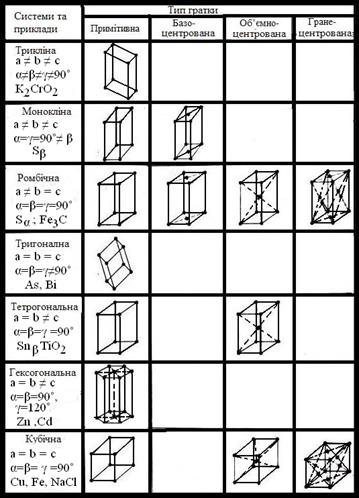
Рисунок 3.1 – Гратки Браве та їх розподіл по сингоніям
Кристали, що складаються з двох або більше елементів, мають декілька простих граток Браве, що взаємно проникають. Так, наприклад, кристалічна гратка 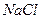 являє собою дві гранецентровані кубічні
являє собою дві гранецентровані кубічні  гратки Браве (одна із іонів
гратки Браве (одна із іонів  , а друга -
, а друга - 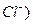 , які вставлені одна в одну та зрушені на ½ просторової діагоналі (рис.3.2,а). Кристалічна гратка
, які вставлені одна в одну та зрушені на ½ просторової діагоналі (рис.3.2,а). Кристалічна гратка  (рис.3.2,б) – такі ж самі
(рис.3.2,б) – такі ж самі  які вставлені одна в одну та зрушені на ¼ просторової діагоналі.
які вставлені одна в одну та зрушені на ¼ просторової діагоналі.
ПРАКТИЧНА ЧАСТИНА
На рис. 3.2 наведені речовини, для яких потрібно визначити – базис гратки; координаційні радіуси та координаційні числа першої і другої координаційної сфер і площини щільнішого пакування.
МЕТОДИЧНІ ВКАЗІВКИ
1. Координаційне число – це число атомів, що розташовані навколо даного атому на найближчій відстані, тобто стикаються одне з одними.. Ці атоми утворюють першу координаційну сферу. Атоми, що розташовані на більш дальшій відстані утворюють другу координаційну сферу.
2. Радіус першої координаційної сфери – це відстань між центрами центрального атому, та центру атому першої координаційної сфери, а відстань до центру атому другої координаційної сфери – це радіус другої координаційної сфери.
3. Базис гратки характеризує кількість атомів, що приходяться на одну елементарну комірку, а також координати цих атомів.
4. Площини щільнішого пакування – це площини, де укладені в гратці найщільнішим способом.
5. Завдання для практичних занять наведені в додатку Б.
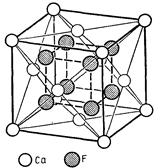
| Структурний тип | А1 – Сu ГЦК | Na – CI Галит | СаF2 |
| Ескіз елементарної чарунки | 
| 
| 
|
| Модель структури | 
| 
| 
|
| Базис гратки (n) | |||
| Координаційне число1 та 11 координаційних сфер та їх радіуси | |||
| Площина щільнішого пакування |
Рисунок 3.2 – Основні типи кристалічних структур
| Структурний тип | А1 – W ОЦК | СsC1 | A3 – Mg ГЩС |
| Ескіз елементарної чарунки | 
| 
| 
|
| Модель структури | 
| 
| 
|
| Базис гратки (n) | |||
| Координаційне число1 та 11 координаційних сфер та їх радіуси | |||
| Площина щільнішого пакування |
Продовження рисунку 3.2.
ЛАБОРАТОРНА РОБОТА №1
ВИЗНАЧЕННЯ ЕЛЕМЕНТОВ СИМЕТРІЇ ТА ПРОСТИХ ФОРМ КРИСТАЛІВ
Мета роботи : навчитися самостійно визначати елементи симетрії, прості форми і сингонію кристалічних многогранників.
ТЕОРЕТИЧНА ЧАСТИНА
1.1Симметрія кристалів
Як зовнішня форма кристалів, так і його внутрішня будова підкорюються одному із всеосяжних законів природи – симетрії. Саме симетрія визначає закони розташування структурних елементів у просторовій гратці, взаємне розташування граней макроскопічного кристала і диктує, за якими напрямками і які фізичні властивості можуть бути у кристалах. Саме знання елементів симетрії кристалів дозволяє виявити у ньому специфічні кристалографічні напрямки, вздовж яких спостерігаються максимальні значення фізичних властивостей (міцності, теплопровідності, електропровідності і т.д.). Прогнозування властивостей кристалів, областей їх застосування дозволяє здійснити їхня симетрія. Тому симетрія є найбільш загальною властивістю кристалічного тіла, а її дослідження – однією із важливих завдань кристалографії. Властивість симетрії є проявом загальних фундаментальних законів природи.
Іншими словами, симетрія –здатність кристала закономірно повторювати свої частини у просторі. Отже симетрична фігура складається з рівних, часто повторюваних частин на площині або у просторі і може сполучатися сама з собою внаслідок симетричних перетворень. Операції або перетворення симетрії – це відбиття, обертання, перенесення, які призводять фігуру до самосумісництва. Геометричні образи (точки, прямі, площини), які характеризують окремі симетричні перетворення, називають елементами симетрії.
Симетричність будь-якої фігури, в тому числі і багатогранника, виявляється за допомогою елементів симетрії. У кристалічних багатогранниках присутні наступні елементи симетрії: центр симетрії, осі та площини симетрії.
Центр симетрії (  або
або )
)
Центром симетрії називається точка всередині фігури, яка характеризуються тим, що будь-якапроведена через цю точку пряма по обидва боки від неї на рівних відстанях зустрічає однакові (відповідні) точки фігури. У кристалах, які мають центр симетрії, протилежні грані попарно однакові та паралельні (рис.1.1,б), тобто такі кристали складені із паралельних граней, однакових за розміром та формою і розвернутих
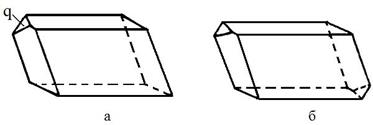
| одна відносно одної на 180˚. Щоб переконатися у наявності центра симетрії, необхідно покласти кристал або його модель на стіл; якщо при всяких положеннях кристала зверху виявляється грань рівна та паралельна (обернено паралельна) нижній грані, то центр симетрії присутній. |
Рисунок 1.1 – Багатогранник без центра симетрії (а) – грань  не має паралельної та рівної їй грані; багатогранник з центром симетрії (б) – кожній грані відповідає паралельна та рівна їй грань не має паралельної та рівної їй грані; багатогранник з центром симетрії (б) – кожній грані відповідає паралельна та рівна їй грань
|
Якщо хоч би для одної грані не знайдена відповідна їй грань, то центр симетрії відсутній (рис. 1.1,а).
Площини симетрії ( 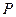 або
або  )
)
Площиною симетріїназивають уявну площину, котра поділяє фігуру на дві дзеркально однакові частини, розташовані одна відносно одної як предмет та його дзеркальне відбиття.

| Площини симетрії проходять або вздовж ребер кристала, утворюючи при цьому рівні кути з обома гранями, що суміжні по даному ребру; або через бісектрису кута між ребрами кристала ,що перетинаються; або перпендикулярно одній з граней кристала, поділяючи його на дві дзеркально рівні частини. На рис.1.2 наведені приклади проведення площин симетрії у кристалічних багатогранниках. |
Рисунок 1.2 – Три площини симетрії (  ) в прямокутному паралелепіпеді, які проведені через середини граней перпендикулярно до них ) в прямокутному паралелепіпеді, які проведені через середини граней перпендикулярно до них
|
Осі симетрії ( 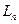 або
або 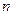 )
)
Віссю симетрії називається уявна пряма, при обертанні навколо якої на деякий кут, фігура сполучається сама з собою. Порядок осі симетрії nвизначає кількість самосполучень фігури при її обертанні на 360оС. Кут повороту, при якому відбувається самосполучення, називається елементарним кутом повороту  .Порядок осі симетрії одночасно зв’язаний з елементарним кутом повороту, який виражається в градусах, співвідношенням:
.Порядок осі симетрії одночасно зв’язаний з елементарним кутом повороту, який виражається в градусах, співвідношенням:  .
. 
У кристалічних багатогранниках присутні лише осі симетрії першого, другого, третього, четвертого та шостого порядків. Елементарній кут повороту для цих осей складає 360, 180, 120, 90 та 60о відповідно. Так як в кристалах можливо провести нескінченну кількість осей симетрії першого порядку (фігура довільної форми після обертання навколо будь-якої осі на 360о обов’язково самосполучиться), то ці осі у кристалах не визначаються.
У кристалах відсутні осі симетрії 5-го та вище 6-го порядку, що обумовлено закономірною внутрішньою будовою кристалів. При наявності, припустимо, у кристалах осей 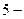 го
го 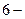 го та
го та  го порядків матеріальні частинки повинні були б розташовуватися у вершинах правильних п’яти - , семи - або восьмикутників, При такому розташуванні вузлів плоска сітка не може бути побудована без просвітів. Наявність таких просвітів надавало б можливість переміщення частинок, тобто привело б до нестабільності структури. В той же час правильні трикутники та шестикутники, а також квадрат та прямокутник цього не дозволяють (рис. 1.3).
го порядків матеріальні частинки повинні були б розташовуватися у вершинах правильних п’яти - , семи - або восьмикутників, При такому розташуванні вузлів плоска сітка не може бути побудована без просвітів. Наявність таких просвітів надавало б можливість переміщення частинок, тобто привело б до нестабільності структури. В той же час правильні трикутники та шестикутники, а також квадрат та прямокутник цього не дозволяють (рис. 1.3).

Рисунок 1.3 – Площинні сітки, які складені із багатогранників 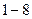 порядків
порядків

| Осі симетрії проходять крізь середини граней та середини ребер, а також крізь середину граней або ребер і вершину, крізь вершини. На рис.1.4 наведені приклади проведення осей симетрії у кристалічному багатограннику. |
Рисунок 1.4 − Багатогранники з осями симетрії:  (а) та (а) та  (б) (б)
|
Класом або видом симетрії будь-якого об’єкту називають сукупність елементів симетрії цього об’єкту. Уся багатообразність симетрії кристалічних многогранників та їхніх фізичних властивостей описується 32 класами симетрії, що об’єднані в сім кристалографічних сингоній або систем, які в свою чергу поділяються на три категорії: нижчу середню та вищу. сингоній. Сингонія(в перекладі з грецької) означає східнокутовість. Сингонією називається сукупність класів симетрії, що мають однакову координатну систему та що об’єднують однакові елементи симетрії. В одну сингонію об’єднується декілька класів симетрії, які мають один або декілька подібних елементів симетрії при однаковій кількості одиничних напрямків (табл.1.1).
32 класи симетрії
Таблиця 1.2 - 32 класи симетрії
| Сингонія | Назва класів, формули симетрії та міжнародні символи | ||||||
| примітивний | центральний | планальний | аксіальний | планаксіаль-ний | інверсійно - примітив ний | інверсійно - планальний | |
| Триклинна | L1 |
C

| |||||
| Моноклінна | Р m | L2 | L2PC 2/m | ||||
| Ромбічна | L22P mm2 | 3L2 | 3L23PC mmm | ||||
| Тригональна | L3 |
L3C
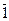 
| L3P 3m | L33L2 | L33L23PC mmm | ||
| Тетрагональна | L4 | L4PC 4/m | L44P 4mm | L44L2 | L44L25PC 4/mmm |
L  ( (  L2) L2)

|
L  ( (  L2)2L22P L2)2L22P
 2m 2m
|
| Гексагональна | L6 | L6PC 6/m | L66P 6mm | L66L2 | L66L27PC 6/mmm |
L 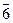 (=L3P) (=L3P)
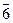
|
L63L33P
(=L33L24P)  2m 2m
|
| Кубічна | 3L24L3 | 3L24L33PC m3 |
3L  4L36P 4L36P
 3m 3m
| 3L44L36L2 | 3L44L36L29PC m3m |
1.2 Прості форми кристалів
Під зовнішньою формою (габітусом кристалів) розуміють сукупність всіх його граней. Сукупність граней, які одержують з однієї заданої грані за допомогою симетричних перетворень, називається простою формою.Всі грані простої форми симетрично рівні не тільки геометрично (за своєю формою), але також за фізичними та хімічними властивостями.
Якщо кристал утворений декількома видами граней, то його зовнішня форма є комбінацією декількох простих форм. Комбінацієюназивається сукупність двох або декількох простих форм, об’єднаних елементами симетрії (рис.2.8).
Прості форми можуть бути як відкритими, так і закритими. Якщо сукупність граней простої форми не замикає простір, то вона називаєтьсявідкритою, якщо простір замикається – то закритою.
До відкритих простих форм відносяться моноедри, пінакоіди, диедри, призми та піраміди. До закритих простих форм відносяться дипіраміди, скаленоедри, трапецоедри, ромбоедр, а також куб, октаедр, тетраедр, ромбододекаедри та їх похідні. Кожний клас симетрії характеризується відповідними йому простими формами. Одна й та ж проста форма може зустрічатися у декількох класах симетрії. Число граней, які входять у одну просту форму, різне і в залежності від виду простої форми змінюється від одиниці (моноедр) до 48 (гексаоктаедр). Розглянемо прості форми.
Моноедр – проста форма, яка складається усього з однієї грані. Пінакоід складається з двох паралельних граней; диедр – із двох граней, що перетинаються між собою. Ці прості форми властиві кристалам нижчої категорії, в той же час моноедри та пінакоіди можуть бути присутніми і в кристалах середньої категорії.
Призми – прості форми, які складаються із чотирикутних граней, які перетинаються по паралельних ребрах. Піраміди складаються із рівних трикутних граней, які перетинаються в одній точці. Дипіраміди являють собою складені своїми основами дві піраміди. Призми, піраміди та дипіраміди поділяються за формою поперечного перетину на ромбічні, тригональні, дитригональні, тетрагональні, дитетрагональні, гексагональні та дигексагональні.
Трапецоедри – це прості форми, що подібні до пірамід, але на відміну від пірамід проти кожної грані розташовані ребра.
Куб (гексаедр) – це проста форма, що складається з шести рівних квадратних граней.
Тетраедри – прості форми, що складаються із чотирьох непаралельних трикутних граней. В залежності від виду трикутної грані розрізняють кубічний тетраедр (рівносторонні трикутники), тетрагональний тетраедр (рівнобедрені трикутники) та ромбічний тетраедр (косокутні трикутники. Виходячи з цього тетраедри можуть відноситися до усіх трьох категорій.
Октаедр – проста форма, що складається з восьми граней – рівнобічних трикутників.
Ромбоедр – що являє собою куб, стиснутий або розтягнутий вздовж тілесної діагоналі.
Ромбододекаедр − проста форма, що складається з дванадцяти рівних граней у формі ромба.
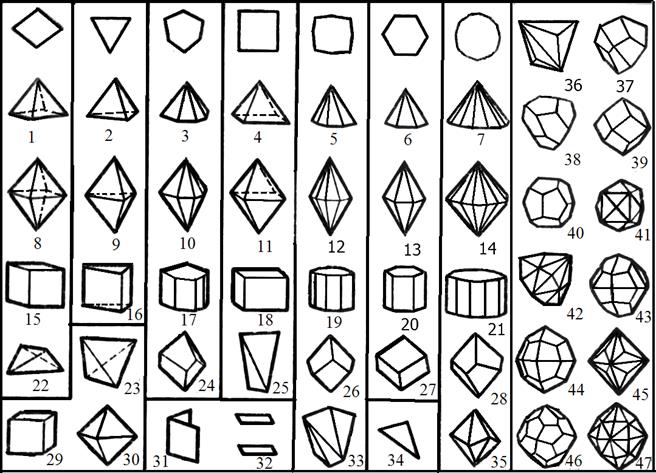
Рисунок 1.5 – Прості форми кристалів
1 – ромбічна піраміда; 2 – тригональна піраміда; 3 – дитригональна піраміда; 4 – тетрагональна піраміда; 5 – дитетрагональна піраміда; 6 – гексагональна піраміда; 7 – дигексагональна піраміда; 8 – ромбічна дипіраміда; 9 – тригональна дипіраміда; 10 – дитригональна дипіраміда; 11 – тетрагональна дипіраміда; 12 – дитетрагональна дипіраміда; 13 – гексагональна дипіраміда; 14 – дигексагональна дипіраміда; 15 – ромбічна призма; 16 – тригональна призма; 17 – дитригональна призма; 18 – тетрагональна призма; 19 – дитетрагональна призма; 20 – гексагональна призма; 21 – дигексагональна призма; 22 – ромбічний тетраедр; 23 – тетраедр; 24 – тригональний трапецоедр; 25 – тетрагональний тетраедр; 26 – тетрагональний трапецоедр; 27 – ромбоедр; 28 – гексагональний трапецоедр; 29 – куб; 30 – октаедр; 31 – діедр; 32 – пінакоїд; 33 – тетрагональний скаленоедр; 34 – моноедр; 35 – дитригональний скаленоедр; 36 – тригон-тритетраедр; 37 – тетрагон-тритетраедр; 38 – пентарон-тригеграедр; 39 – ромбододекаедр; 40 – пентагон-додекаедр; 41 – тетрагексаедр; 42 – гексатетраедр; 43 – дидодскаедр; 44 – тетрагон-триоктаедр; 45 – тригон-триоктаедр; 46 – пенгагон-триоктаедр; 47 -гексаоктаедр.

| Особливе положення займають прості форми вищої категорії, тому що кубічні кристали ограновуються за допомогою своїх п'ятнадцяти простих форм, які умовно поділяють на три групи по п`ять простих форм у кожній. Це група гексаедра – куба, група октаедра та група тетраедра (кубічного). Всі прості форми кожної групи можуть бути отримані із основного багатогранника за допомогою деформації (невеликої) |
| а – тетрагональна призма та тетрагональна дипіраміда; б – ромбододекаедр та куб б – ромбододекаедр та куб Рисунок 1.6 − Комбінації простих форм |
кількості його граней. Особливе положення займають прості форми вищої категорії, тому що кубічні кристали ограновуються за допомогою своїх п'ятнадцяти простих форм, які умовно поділяють на три групи по п`ять простих форм у кожній. Це група гексаедра – куба, група октаедра та група тетраедра (кубічного). Всі прості форми кожної групи можуть бути отримані із основного багатогранника за допомогою деформації (невеликої) його граней.
На кристалах, як правило, спостерігаються грані, які належать до декількох простих форм. Це, так звані, комбінації простих форм. В той час як простих форм налічується тільки 47, комбінацій простих форм – безліч. Цілком ясно, що відкриті прості форми можуть бути тільки у комбінації з іншими простими відкритими або закритими формами; закриті прості форми можуть бути як у чистому вигляді, так і в комбінаціях (рис.2.9). Число простих форм, які реально спостерігаються на кристалах, рідко перевищує 3 - 5.

| Таким чином, усю сукупність граней ідеального кристалічного багатогранника можливо поділити на сукупність граней, які симетрично дорівнюють одна одній Переважний розвиток тієї або іншої простої форми в комбінаціях залежить від умов росту. Найбільш розвинутими на кристалі виявляються грані тих простих форм, для яких швидкість росту мінімальна. |
а – кальцит; б - арагоніт
Рисунок 1.7 − Природні форми кристалів  : :
|
На рис. 1.8 наведені представники кристалів за 32 класами симетрії та їх характеристична форма.в.
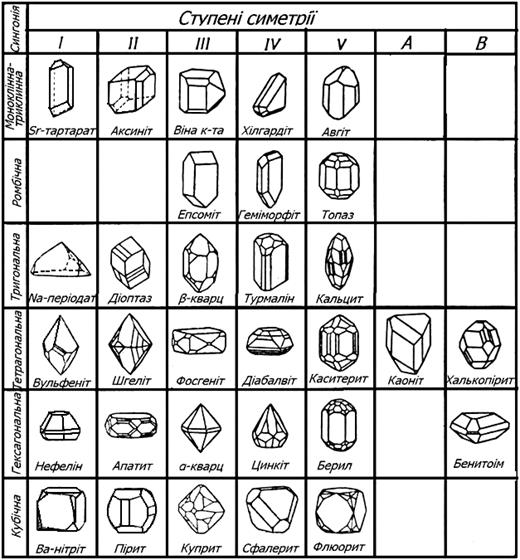
Рисунок 1.8 – Характеристична зовнішня форма кристалів за 32 класами симетрії.
2 ПОРЯДОК ВИКОНАННЯ РОБОТИ
1.Визначити всі елементи симетрії даної моделі кристалу.
2. По сукупності елементів симетрії встановити клас симетрії, категорію та сингонію кристалу (додаток Б).
3. Визначити характерні елементи симетрії даної сингонії.
4. Намалювати модель та показати на ній всі елементи симетрії.
5. Визначити число та назви простих форм, що входять до даної комбінації.
3 МЕТОДИЧНІ ВКАЗІВКИ
При визначенні елементів симетрії кристалів за їх зовнішньою формою (огранкою) слід пам’ятати, що:
1. Спочатку слід виявити осі симетрії вищого порядку (вище другого), а після цього вже переходити до визначення осей другого порядку та інших елементів симетрії (площин симетрії та центру симетрії). Осі симетрії вищого порядку проводять через вершини, де сходяться рівні ребра, або через центри граней з числом ребер, кратним порядку осі симетрії.
2. При визначенні осей симетрії потрібно намагатися не перевертати модель кристалу, бо це може призвести до помилки у підрахунку числа однорідних елементі симетрії.
Щоби розібратися з простими формами та їх комбінаціями необхідно:
1. Визначити число простих форм, з яких складається модель кристалу – воно дорівнює числу різноманітних граней моделі, що досліджується.
2. Виявити та порахувати число граней кожної простої форми.
3. Визначити назву кожної простої форми, що входять до даної комбінації. Ґждя визначення простої форми слід уявно подовжити всі грані даної форми до взаємного перетину.
ЛАБОРОТОРНА РОБОТА №2
СТЕРЕОГРАФІЧНІ ПРОЕКЦІ ЕЛЕМЕНТОВ СИМЕТРІЇ
ТА ПРОСТИХ ФОРМ
Мета роботи : вивчити принцип стереографічного проектування та побудувати стереографічні проекції елементів симетрії та простих форм кристалів різних сингоній
1 ТЕОРЕТИЧНА ЧАСТИНА
При вирішенні ряду задач кристалографії, рентгеноструктурного та електронографічного аналізів користуються проекцією кристалічних багатогранників та їх елементів симетрії. Проекції, які прийняті в кристалографії, дозволяють не тільки наочно зображати кристал, але й проводити вимірювання двогранних кутів. Як відомо, при зростанні кристала може змінюватися його зовнішній вигляд (розміри та форма граней), але кути поміж відповідними гранями залишаються незмінними. Тому форму кристалічного багатогранника, розташування його елементів симетрії, а також анізотропію властивостей можливо охарактеризувати набором кутів між гранями.
Найбільш розповсюджені стереографічні проекції елементів симетрії і гномостереографічні проекції граней кристала. Ознайомимось із їх сутністю (рис.2.17).
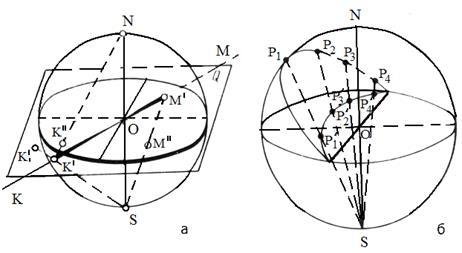
Рисунок 2.1 – Стереографічні проекції напрямку (а) і площини (б)
Для побудови стереографічної проекції із точки  – центра кристала задовільним радіусом опишемо кулю, яка називається сферою проекцій. Через точку
– центра кристала задовільним радіусом опишемо кулю, яка називається сферою проекцій. Через точку  проведемо горизонтальну (екваторіальну) площину
проведемо горизонтальну (екваторіальну) площину  – площину проекцій. Велике коло,по якому перетинається при цьому сфера проекцій, має назву коло проекцій. За вісь проекцій обираємо вертикальний діаметр сфери проекцій
– площину проекцій. Велике коло,по якому перетинається при цьому сфера проекцій, має назву коло проекцій. За вісь проекцій обираємо вертикальний діаметр сфери проекцій 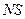 , який перпендикулярний площині проекцій
, який перпендикулярний площині проекцій 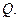 Точки перетину
Точки перетину  та
та 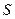 називаються точками зору.
називаються точками зору.
Для отримання кристалографічної проекції деякого напрямку 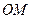 його подовжують до перетинання зі сферою проекцій (див. рис.2.17.а). Отриману точку
його подовжують до перетинання зі сферою проекцій (див. рис.2.17.а). Отриману точку  з`єднують прямою із точкою зору
з`єднують прямою із точкою зору  Точка перетинання
Точка перетинання  променя зору
променя зору 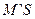 із площиною проекцій є стереографічною проекцією напрямку
із площиною проекцій є стереографічною проекцією напрямку 
Якщо напрямок  , що проектується, перетинає сферу проекцій у нижній півсфері, то за точку зору приймають
, що проектується, перетинає сферу проекцій у нижній півсфері, то за точку зору приймають  . Для того щоб відрізнити точки проекцій, що належать різним півсферам, необхідно відзначати їх кружечками (верхня півсфера) і хрестиками (нижня півсфера).
. Для того щоб відрізнити точки проекцій, що належать різним півсферам, необхідно відзначати їх кружечками (верхня півсфера) і хрестиками (нижня півсфера).
Таким чином стереографічні проекції напрямків зображуються точками всередині кола проекцій. Вертикальний напрямок проектується у центрі кола проекцій, а горизонтальні – як дві точки на екваторі (рис.2.18,1).
Осі симетрії проектуються як напрямки.
| Для того щоб побудувати стереографічну проекцію площини, її необхідно перенести паралельно самій собі у центр кола проекцій та продовжити до перетинання з поверхнею сфери проекцій (рис. 2.18,б). Внаслідок перетинання отримуємо дугу великого кола, з’єднавши яку променями зору із точкою зору  отримаємо конічну поверхню із вершиною в полюсі проекцій отримаємо конічну поверхню із вершиною в полюсі проекцій 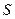 . Слід перетинання цієї конічної поверхні із площиною проекцій дає стереографічну проекцію площини, яка являє собою кругову дугу. Зазвичай проектують лише частину площини, що перетинає верхню півсферу. . Слід перетинання цієї конічної поверхні із площиною проекцій дає стереографічну проекцію площини, яка являє собою кругову дугу. Зазвичай проектують лише частину площини, що перетинає верхню півсферу.
|
| Рисунок 2.2 – Стереографічні проекції: I - напрямків (або гномостереографічні проекції площин); II – площин, які розташовані: а – перпендикулярно, б – паралельно, в – під кутом до площини проекцій |
Стереографічні проекції горизонтальних площин представляють собою коло, яке співпадає з границями кола проекцій, проекції вертикальних площин співпадають з діаметром кола проекцій, а проекції похилих площин симетрії зображуються дугами, які спираються на кінці діаметру круга проекцій (рис. 2.18,II).
Стереографічні проекції застосовуються головним чином для зображення елементів симетрії кристалів. При стереографічному проектуванні кристалічний багатогранник розташовується строго визначеним чином у сфері проекції. Кристали кубічної сингонії розташовують таким чином, щоб одна із трьох осей  була вертикальною, а дві інші повинні лежати у горизонтальній площині, при цьому одна з них направляється на спостерігача, а друга – паралельна йому. При відсутності осей
була вертикальною, а дві інші повинні лежати у горизонтальній площині, при цьому одна з них направляється на спостерігача, а друга – паралельна йому. При відсутності осей  аналогічним чином розташовуються подвійні осі симетрії.
аналогічним чином розташовуються подвійні осі симетрії.
Кристали середньої категорії розташовуються таким чином, щоб осі вищого порядку  суміщалися з віссю проекцій.
суміщалися з віссю проекцій.
В кристалах ромбічної сингонії присутні три одиничних напрямки, які співпадають з осями другого порядку або з нормалями до площин симетрії. Одне із одиничних напрямків, що співпадає з віссю 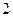 , суміщають із віссю проекцій, а два інших лежать у горизонтальній площині, одне з них направлено на спостерігача, а інше – паралельно йому.
, суміщають із віссю проекцій, а два інших лежать у горизонтальній площині, одне з них направлено на спостерігача, а інше – паралельно йому.
При проектуванні кристалів моноклінної сингонії вісь симетрії 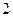 або нормаль до площини симетрії, які являються одиничними напрямками, розташовуються паралельно колу проекцій.
або нормаль до площини симетрії, які являються одиничними напрямками, розташовуються паралельно колу проекцій.
Осі симетрії проектуються як напрямки. Вертикальні осі зображуються в центрі кола проекцій, горизонтальні, що співпадають з площиною креслення, дадуть два виходи на колі проекцій; похилі осі проектуються всередині кола проекцій (рис. ). Виходи осей

| симетрії на проекції зображуються особливими значками, що відображують порядок осі симетрії. Наявність центру симетрії відзначається значком С у центрі кола проекцій. Стереографічні проекції площин симетрії є дугами та зображуються подвійними лініями (рис. ). Для проектування кристалічних багатогранників застосовують гномостереографічні проекції, тобто проекції нормалей до граней кристалів. При цьому горизонтальні грані кристалів зображують точкою, яка співпадає з центром проекцій, вертикальні – точками, що лежать на самому колі проекцій, а похилі – точками, які знаходяться у колі проекцій і розташовуються тим дальше від центру, чим круче похил цієї грані . |
| Рисунок 2.3 – Позначення елементів симетрії на стереографічній проекції |

| Рисунок 2.4 – Проектування кристала методом стереографічних проекцій (а); зображення проекцій граней А, В,С і D на площину Q (б) |
Принцип побудови гномостереографічної проекції зводиться до наступного (рис.2.4 ).
Кристал розміщується в центрі круга проекцій. Через центр сфери, суміщеної з центром кристалу до кожної його грані відбудовується нормаль, наприклад Оа1до перетинання її з поверхнею сфери. Отриману точку а, тобто полюс грані а з’єднують прямою з точкою зору S. Екваторіальна площина Q – площина проекцій, Лінії, що з’єднують полюси граней з точками зору S або N, перетинають цю площину в певній точці, що являє собою проекцію нормалі до грані а. Щоб побудувати гномо стереографічні проекції нормалей, що перетинають кулю в нижній півсфері, точку зору переносять у північний полюс сфери N. Проекції нормалей до граней кристалу (гномо стереографічні проекції), що знаходяться в нижній півсфері, позначаються хрестиками, а в верхній півсфері - кружалками (рис. ,б).
2 ПОРЯДОК ВИКОНАННЯ РОБОТИ
1. Визначити всі елементи симетрії та прості форми даної моделі.
2. Встановити сингонію та категорію кристалу.
3. Замалювати модель і показати на ній елементи симетрії.
4. Спроектувати всі елементи симетрії і грані моделі кристалу.
ЛАБОРАТОРНА РОБОТА №3
ДІАГНОСТИКА МІНЕРАЛІВ ЗА ЇХ ФІЗИЧНИМИ ВЛАСТИВОСТЯМИ
Мета роботи: вивчити і описати зовнішні признаки – морфологію та фізичні властивості мінералів.
1 ТЕОРЕТИЧНА ЧАСТИНА
Мінералом (у даний час) називається хімічно і фізично індивідуалізований неорганічний продукт природної фізико-хімічної реакції, що знаходиться в кристалічному стані або був у кристалічному стані і втратив його в результаті метаміктного розпаду.
Тобто мінерали являють собою хімічні елементи, що утворюються в результаті різноманітних фізико-хімічних процесів, що протікають у земній корі.
До мінералів відносять також складові частини інших космічних тіл - метеоритів, планет і їх супутників.
До мінералів також відносять кристалічні продукти життєдіяльності різних організмів, після відмирання яких з цих мінералів утворюються скупчення мінеральної сировини (наприклад, фосфоритів).
Відомо понад 3000 мінеральних видів і приблизно така ж кількість різновидів. Щорічно відкривають декілька десятків мінералів. Широко розповсюджені в природі близько 450 видів, решта ж зустрічаються рідко.
Кожному мінералу притаманний певний комплекс фізико-механічних властивостей, за якими він відрізняється від інших мінералів і, отже, може бути визначеним, тобто діагностованим.
Нині немає жодної галузі народного господарства, де б у томучи іншому вигляді не використовувалися мінерали.
Розвиток металургійної промисловості тісно пов'язаний із використанням мінералів. Всеюічне вивчення складу мінералів є основою умови правильного комплексного використання їх.
Деякі властивості одного й того ж мінералу можуть змінюватися у залежності від додавання домішок тощо. Тому при визначенні мінералів за зовнішніми признаками визначають не одну яку-небудь властивість, а комплекс властивосте , що характеризують даний мінерал: габітус, складання, колір, колір риски, блиск, спайність, злам, прозорість та ін.. Колір, блиск та колір риски є скалярними властивостями в той час як інші властивості (твердість, спайність і т.д.) є векторними властивостями.
1.1 Вигляд кристалів або кристалічних зерен (габітус)
Якщо габітус (вигляд, зовнішня форма) мінералу являє собою правильний багатогранник, то для характеристики габітусу використовують кристалографічні найменування – кубічний, октаедричний, ромбоедричний тощо.
У випадку неясної форми мінералу за зовнішністю (габітусу) кристали поділяють на три типи :
1) ізометричні - мають приблизно однакові розміри по трьом взаємно перпендикулярним напрямам (гранат);
2) витягнуті по двох напрямах (сплощенні): стовпчасті (барит, гематит), пластинчасті, листуваті, лускаті (слюда, тальк, хлорит);
2) витягнуті в одному напрямку: стовпчасті (кварц, берил, актиноліт), шестоваті (кальцит), волокнисті (селеніт), голкові (турмалін, рутил).
1.2 Складання (характер зростків або агрегатів)
Залежно від хімічного складу і умов утворення мінерали нерідко утворюють вельми характерні по вигляду скупчення зерен або кристалів, що мають назву мінеральні агрегати.
Агрегати можуть складатися з кристалічних зерен одного мінералу, тобто є мономінеральними (наприклад, штуф магнетитової руди або мармуру). Полімінеральні агрегати складаються з кристалічних зерен, представлених декількома різними мінералами (наприклад, кусок граніту).
Розглянемо основні типи мінеральних агрегатів.
I. Зернисті агрегати є найпоширенішими; ними складені всі кристалічні породи. Вони є скупченнями неправильно зрощених зерен, за величиною яких розрізняють наступні агрегати:
- грубозернисті - розмір зерен більш 5мм; середньозернисті - із зернами 1-5 мм, легко помітні неозброєним поглядом;
- дрібнозернисті - розмір зерен до I мм, зерна помітні тільки за допомогою лупи і мікроскопа в шліфах;
- скритнокристалічні або щільні - окремі зерна не можна розрізнити навіть у лупу, їх будова може бути встановлена тільки за допомогою мікроскопа.
За відносною величиною кристалічних зерен розрізняють рівномірно- і нерівномірно зернисті агрегати.
За ступенем заповнення простору розрізняють щільні і рихлі (землисті) агрегати. Землисті агрегати нагадують своїм виглядом шматки рихлої породи і характерні для порошковатих рихлих мінералів і для осадкових порід (глин, бокситів, бурих залізняків, марганцевих руд і так далі).
Залежно від форми зерен, що складають агрегат, розрізняють листуваті, стовпчасті, волокнисті, пластинчасті і інші агрегати. Коли агрегат складний зернами більш менш ізометричної форми, його називають зернистим.
Листуваті, пластинчасті, лускаті агрегати (рис. 8.15) складені індивідами пластинчастої, листуватої або лускатої зовнішності (слюда, хлорит, барит). При цьому враховуються розміри індивідів. Залежно від розташування індивідів складання агрегатів

| характеризується як паралельно-листувате (пластинчасте або лускате), радіально-листувате (пластинчасте або лускате) і безладно листувате (пластинчасте або лускате). Стовпчасті, голчасті, волокнисті агрегати складені індивідами (зернами), що мають витягнуту в одному напрямку форму. Залежно від взаємного розташування індивідів розрізняють |
| Рисунок 3.1 – Пластинчасті агрегати мінералу |
агрегати паралельно-, радіально- і безладно- або заплутано-листуваті (голчасті або волокнисті (рис. 4.2).
2. Друзи - групи кристалів одного або різних мінералів, що наросли своїми основинами на плоску або увігнуту поверхню (рис. 4.3). Таким чином, друзами є зростки добре утворених кристалів. Розрізняють два типи друз: I) друзи наростання і 2) друзи перекристалізації.

| 
|
| Рисунок 3.2 – Стовпчасто-голчасті кристали антимоніту на друзах кварцу | Рисунок 3.3 – . Друза кристалів кварцу |
Для друзи наростання характерна наявність певної поверхні породи,що вміщує та на яку наростають кристали мінералу в результаті кристалізації речовини, що привноситься розчинами у вільному просторі.
У друзах перекристалізації відсутня поверхня, від якої починають зростання всі, вхідні в друзу кристали. У них спостерігається, безперервний перехід від породи, що вміщує, до друзи.
3. Дендрити утворюються при швидкій кристалізації мінералів, а також при кристалізації в тонких волосяних тріщинах породи або у в'язкій речовині (у мокрій глині). Форма дендритів гілляста деревовидна, схожа на відбитки рослин (рис. 8.18). Дендрити, на відміну від скелетних форм монокристалів, складаються з окремих кристалічних індивідів, зрощених в двійниковому або паралельному положенні. Дуже часто зустрічаються чорні дендрити оксидів марганцю, а також самородної міді, золота, срібла.
- Конкреції (рис. 4.4) - частіше кулясті утворення або не зовсім правильної форми сферичні стягнення і жовна, що виникають в результаті відкладення речовини навколо певних центрів. Розміри конкрецій коливаються у широких межах - від декількох міліметрів до десятка сантиметрів, а іноді і до метрів в поперечнику.
- Секреції - мінеральні утворення, що заповнили порожнечі в гірських породах (рис.4.5). На відміну від конкрецій, що ростуть від якогось центру до периферії, зростання секрецій відбувається від периферії до центру шляхом відкладення речовини на стінках порожнечі. Форма секрецій зазвичай овальна. Залежно від розміру секреції носять назву жеод (діаметр більш 1-2 см) або мигдалин (до 10 мм в поперечнику).

|
|
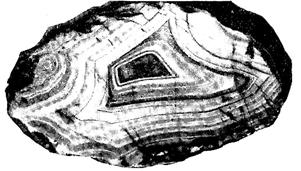
| Рисунок 3.4 – Конкреції фосфоритів | Рисунок 3.5 – Полосчастість агату |
5. Натічні форми мінеральних утворень виникають за рахунок колоїдів - гелів, які обволікають стінки порожнин, поступово втрачають воду, що випаровується в порожній простір, густіють і під дією сили тяжіння звисають вниз і кристалізуються у вигляді затверділих стовпчастих (сталактитів), ниркоподібних, гроноподібних і інших утворень Сталагміти, на відміну від сталактитів, є стовпчастими утвореннями, зростання яких відбувається від низу до верху за рахунок падаючих крапель колоїдних розчинів. Розміри сталактитів і сталагмітів коливаються у вельми широкому інтервалі, починаючи від мікроскопічних і кінчаючи товстими стовпоподібними утвореннями арагоніту і кальциту у великих печерах.
Крупні кулясті маси неправильної форми з блискучою поверхнею носять назву скляні голови - бура і червона скляні голови характерні для бурого і червоного залізняка відповідно (рис. 8.21,а).
Натічні утворення часто характеризуються концентрично-зональною будовою. У натічних формах зустрічаються різні мінерали: опал, малахіт, гіпс, арагоніт, кальцит, гідроокиси заліза (лимоніт, гетит) і марганцю (псиломелани), сульфіди різних металів і ін. (рис. 8.22, 8.23)

|
 в
в
|
| Рисунок 3.6 − Гідрогетит : а – бура скляна голова; б – натічні сталактитові утворення; бруньковидні агрегати арагоніту (в) |
Деревовидні, пір’ясті, в’язані форми агрегатів характерні для деяких самородних металів, окислів заліза та марганцю, галоїдних солей. Деякі з цих утворень

| нагадують відбитки рослин (рис. 4.7). Землисті агрегати – пухкі маси слабко пов’язаних поміж собою часток. Що легко розпадаються на дрібні грудочки, складаються з дрібних зерняток, характерні для багатьох осадкових порід, глин, бурих залізняків. Марганцевих руд, бокситів і т.д. |
| Рисунок 3.7 – Самородна мідь |
Дата добавления: 2015-06-10; просмотров: 4816;
