Прозорість
Прозорість мінералу - властивість пропускати крізь себе світло. За здатністю пропускати світло всі мінерали, що спостерігаються в крупних кристалах, ділять на три групи: прозорі - ісландський шпат, флюорит, топаз, кварц і ін.; напівпрозорі - смарагд, сфалерит, кіновар і ін.; непрозорі - магнетит, пірит, графіт і ін.
На відміну від кристалів, в агрегатах мінералів, що складаються з по різному оптично орієнтованих зерен, світло, багато разів заломлюючись в різних напрямах, у результаті розсіюється і відбивається. Тому агрегати мінералів, що складені з прозорих зерен, є непрозорими; їх прозорість може бути виявлена тільки в тонких зрізах (шліфах).
При діагностиці мінералів за їх макроскопічними властивостями використовуються ще і інші фізичні властивості: магнітність, смакові властивості, горючість, механічні властивості (крихкість, пружність, гнучкість, глейкість).
2 ПОРЯДОК ВИКОНАННЯ РОБОТИ
6. Робота виконується на колекції, що а з трьох мінералів.
7. Для кожного мінералу визначається комплекс його фізичних властивостей.
8. Описання мінералів та гірських порід проводиться за схемою, що наведена в табл.
9. Дві останні строки таблиці (походження та практичне значення) студенти повинні знайти у підручниках по мінералогії.
Таблиця 3.1 - Порядок опису мінералів
| Найменування | |||
| Хімічна формула | |||
| Сингонія | |||
| Тип структури | |||
| Облік кристалів | |||
| Морфологія агрегатів | |||
| Колір | |||
| Колір риски | |||
| Блиск | |||
| Твердість | |||
| Ковкість крихкість | |||
| Спайність | |||
| Злам | |||
| Густина | |||
| Походження | |||
| Практичне значення |
.
ЛАБОРАТОРНА РОБОТА №4
ЯКІСНИЙ ФАЗОВИЙ АНАЛІЗ. РОЗШИФРУВАННЯ ПОВНИХ ДІФРАКТОГРАМ
Мета роботи: визначити речовину, з якої була отримана дифрактограма та її параметри – гратку Браве, період кристалічної гратки заданої речовини
ТЕОРЕТИЧНА ЧАСТИНА
Використання променів Рентгена для аналізу кристалічних речовин дозволяє вивчати внутрішню будову кристалів (тип гратки Браве, параметри і викривлення кристалічної гратки,) наявність фаз в кристалічному зразку і їх кількісне співвідношення і так далі, а також визначати приховані дефекти у виробах без їх руйнування.
В даний час за допомогою рентгеноструктурного аналізу вивчені структури не тільки металів, але і більшості нерудних і рудних мінералів, різних проміжних продуктів металургійного виробництва і інших допоміжних матеріалів, що використовуються в чорній металургії.
Рентгенографічні дослідження багатьох продуктів металургійного виробництва (шлаків, штейнів і ін.), а також продуктів, що отримуються при відпалені вогнетривких матеріалів і при взаємодії їх з шлаками і металом, дозволило у багатьох випадках розкрити і пояснити явища, що відбуваються при цьому, і налагодити контроль відповідних технологічних процесів.
Таким чином рентгенівський аналіз – один із найбільш ефективних і універсальних методів вивчення структури і складу будь-якої кристалічної речовини.
Рентгенівське випромінювання є короткохвильовим; довжини хвиль рентгенівських променів, що використовуються для аналізу кристалів, лежать в інтервалі ~0,005–0,25нм. Таким чином, довжини хвиль рентгенівських променів відповідні до міжатомної відстані в кристалах, що забезпечує їх унікальні властивості:
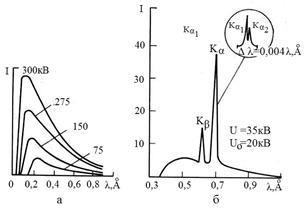
| Як і світлові, рентгенівські промені можуть мати суцільний і лінійчатий спектри (рис.4.1). Випромінювання з суцільним спектром називають іноді білим, а з лінійчатим спектром – характеристичним; промені будь-якої однієї довжини хвилі – монохроматичним. Для рентгеноструктурного аналізу використовують випромінювання |
| а – суцільний спектр; б – характеристичний спектр на фоні суцільного спектра (анод – молібден) Рисунок 4.1 − Спектральні криві |
з характеристичним спектром. Для виникнення дифракційних максимумів у характеристичному спектрі необхідно, щоб хвилі, що відбиваються всіма паралельними атомними площинами, підсилювали одна одну при інтерференції. Ця умова виконується тільки при певних співвідношеннях між довжиною (  ) дифрагуючої хвилі і кутом (
) дифрагуючої хвилі і кутом ( 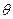 ) її падіння на атомні площини:
) її падіння на атомні площини:
 або
або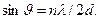
Ця формула − рівняння Вульфа-Бреггів, є основною розрахунковою формулою в рентгенографії.
Якісним фазовим аналізом називається встановлення наявності фаз в зразку, що досліджується, і їх ідентифікація. Рентгенівський якісний фазовий аналіз дозволяє визначити сполучення, з яких складається досліджує мий храпок, та їх різні поліморфні модифікації. Фазовий аналіз застосовується для вивчення вихідних матеріалів металургійного виробництва (руди, продукти збагачення, флюси, агломерати) і продуктів виплавляння ( сталі, чавуну, сплавів і шлаків). Для аналізу вогнетривких матеріалів, металів і сплавів при їх термічній та механічній обробці, продуктів окислення, мінералів тощо.
Рентгенівський фазовий аналіз заснований на тому, що кожна фаза має свою кристалічну гратку зі строго визначеними параметрами і, таким чином, характеризується індивідуальним набором міжплоскостних відстаней. На дифрактограммі (рис.3,б) відбиттю від кожної площини (hkl) відповідає дифракційний максимум при визначених кутах θ.
Для ідентифікації фази, що присутня в зразку, необхідно по дифрактограмі визначити значення міжплощинних відстаней :
 ,
,
де λ – довжина хвилі характеристичного спектру, в якому була проведена зйомка,
θі – кут θ і – го максимуму на дифрактограммі.
Отриманий набір експериментальних значень d/n порівнюють з табличними (довідковими) значеннями d/n передбачених фаз. Порівняння починають з найбільш інтенсивних ліній передбаченої фази. Якщо експериментальні значення d/n співпадають зі значеннями d/n наведеними в довіднику трьох-чотирьох самих інтенсивних ліній передбаченої фази, то її присутність в досліджуємому зразку слід вважати доказаним.
Чутливість фазового аналізу складає 0,1 – 5%.
По дифрактограммі полікристалу можливо визначити сингонію, до якої відноситься зразок , що досліджується, індекси інтерференції максимумі та період кристалічної гратки.
Період кристалічної гратки кристалів кубічної сингонії визначається за формулою:
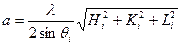 ,
,
де Н2і, К2І, L2i - індекси інтерференції.
Встановлено, що співвідношення квадратів синусів відбиття дорівнює співвідношенню суми квадратів індексів:

Виходячи з цього, можливо скласти ряд співвідношень квадратів синусів для кубічної гратки:
| Примітивна | 1; 2; 3; 4; 5; 6 |
| Об’ємноцентрована | 2; 4; 6; 8; 10; 12 |
| Гранецентрована (ГЦК) | 3; 4; 8; 11; 12 |
Дата добавления: 2015-06-10; просмотров: 897;
