ПРАКТИЧНЕ ЗАНЯТТЯ №2
МЕТОД КРИСТАЛОГРАФІЧНОГО ІНДЕКСУВАННЯ
Кристаламиназивають тверді тіла, що мають натуральну форму багатогранника та характеризуються закономірним розташуванням у просторі елементарних частинок - атомів, іонів, молекул. До них відносяться природні кристали мінералів, що утворилися у земній корі, та синтетичні кристали, отримані у лабораторіях. Кристал може і не мати форму багатогранника, але він, так як і уламок будь-якого кристала, володіє рядом макроскопічних фізичних властивостей, які характерні також і добре огранованому кристалу. Окремі цілісні кристали називають монокристалами , в той же час як агрегати хаотично орієнтованих дрібних кристаликів різного розміру та неправильної формі називають полікристалами.
Кристалічний стан - термодинамічно рівноважний стан твердих тіл. Головною властивістю кристалічного стану є наявність правильного (впорядкованого та симетричного) розташування матеріальних частинок у просторі. Кристалічний стан володіє чіткою просторовою будовою, а кристал - фізичне тіло, котре має ґратчасту (решітчасту) будову, тобто сувору тривимірну періодичність розташування матеріальних частинок. Частинки, з яких складаються кристали, тобто іони, атоми, молекули, комплекси розташовані у просторі закономірно та симетрично. Закономірність розташування частинок, їх природа, їх енергетичний спектр та сили зв'язку між ними визначають фізичні властивості кристалічної речовини. Кожна кристалічна речовина фіксованого хімічного складу має визначену кристалічну структуру.
Ідеальний кристал можливо побудувати шляхом нескінченного закономірного повторювання у просторі однакових структурних одиниць. У найбільш простих кристалах, наприклад, у кристалах заліза, міді, срібла, кристалах лужних металів структурна одиниця (яка часто називається вузлом) складається з одного атому. У кристалах більш складних речовин структурна одиниця може містити в собі декілька атомів або молекул. У кристалах деяких неорганічних речовин структурна одиниця може містити в собі більше 100 атомів або молекул (наприклад, інтерметалеве сполучення  має кубічну комірку, яка містить в собі 1192 атома), а у білкових кристалах це число може досягати 104).
має кубічну комірку, яка містить в собі 1192 атома), а у білкових кристалах це число може досягати 104).
Кристал може складатися із атомів декількох хімічних елементів (наприклад, кристал 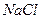 ) або містити в собі зв`язані групи однакових атомів (наприклад,
) або містити в собі зв`язані групи однакових атомів (наприклад, 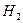 ).
).
Характерне для кристалів трьохмірне періодичне розташування матеріальних частинок можливо наочно зобразити просторовою граткою. Просторова гратка - абстрактний математичний образ, який дозволяє фіксувати розташування матеріальних частинок у просторі. У структурі ідеального кристала усі гомологічні (однаково розташовані) точки розташовуються нескінченними правильними симетричними рядами.
Пряма, яка проходить у кристалічній гратці через два задовільно обраних, але однакових вузла, проходить також через інші вузли гратки та утворює нескінчений одномірний ряд (рис. 1.1,а). Відстань між гомологічними точками у нескінченному ряді 
 називають періодом трансляції, параметром або проміжком ряду.
називають періодом трансляції, параметром або проміжком ряду.
Сукупність двох систем паралельних рядів з параметрами  і
і 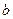 дозволяє отримати сукупність гомологічних точок у вигляді площинної сітки (рис.1. 7,б). Таким чином двомірна площинна сітка визначається двома параметрами (трансляціями)
дозволяє отримати сукупність гомологічних точок у вигляді площинної сітки (рис.1. 7,б). Таким чином двомірна площинна сітка визначається двома параметрами (трансляціями)  і
і 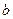 або трьома вузлами, які не лежать на одній прямій. Комірка, сторонами якої є елементарні трансляції (періоди гратки), називається елементарною коміркою площинної сітки. Елементарна комірка примітивна, коли усередині неї відсутні вузли. Так як кожний вузол одночасно належить чотирьом коміркам, то на кожну елементарну комірку припадає тільки один вузол. Кількість вузлів, що припадають на одиницю площини, називається ретикулярною густиною сітки.
або трьома вузлами, які не лежать на одній прямій. Комірка, сторонами якої є елементарні трансляції (періоди гратки), називається елементарною коміркою площинної сітки. Елементарна комірка примітивна, коли усередині неї відсутні вузли. Так як кожний вузол одночасно належить чотирьом коміркам, то на кожну елементарну комірку припадає тільки один вузол. Кількість вузлів, що припадають на одиницю площини, називається ретикулярною густиною сітки.

Рисунок 1.1 − Просторова гратка (в) та її елементи: одномірний ряд (а) і площинна сітка (б)
Таким чином площинна сітка цілком визначена двома рядами і являє собою систему однакових площинних елементарних комірок, які паралельно орієнтовані, прилягають одна до одної та без проміжків заповнюють площину.
Якщо узяти (провести) ще один нескінченний ряд з проміжком 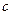 ,який лежить поза площиною креслення, то в цьому випадку вже можливо через три системи паралельних рядів з параметрами
,який лежить поза площиною креслення, то в цьому випадку вже можливо через три системи паралельних рядів з параметрами 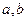 та
та 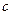 провести три системи паралельних площин. Це дає просторову гратку , тобто тривимірну систему гомологічних точок (рис.1.1,в). Таким чином, просторова гратка може бути подана як три системи паралельних сіток з параметрами (
провести три системи паралельних площин. Це дає просторову гратку , тобто тривимірну систему гомологічних точок (рис.1.1,в). Таким чином, просторова гратка може бути подана як три системи паралельних сіток з параметрами (  і
і 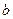 ), (
), (  і
і 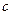 ) та (
) та ( 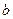 і
і 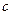 ); ці системи, взаємно перетинаючись, утворюють сукупність паралелепіпедів, які паралельно орієнтовані та суміжні по цілим граням.
); ці системи, взаємно перетинаючись, утворюють сукупність паралелепіпедів, які паралельно орієнтовані та суміжні по цілим граням.
Паралелепіпед, сторонами якого є три параметри (трансляції), називається елементарною коміркою або елементарним паралелепіпедом. Шляхом паралельних перенесень (трансляцій) елементарної комірки можливо заповнити весь простір кристалічної структури. Примітивна комірка – комірка з мінімальним об'ємом, на яку припадає тільки одна гомологічна точка кристалічної решітки. Хоча в кожному з восьми вузлів паралелепіпеда знаходиться точка гратки , але кожна така точка належиться одночасно восьми коміркам, котрі сходяться у точці, що у розглядається.
Просторову гратку кристала слід розглядати як математичну абстракцію, за допомогою якої можливо зручно (математично) описати періодичність кристалічної структури. Гратка відображає симетрію структури, незалежно від того, чи співпадає вузол з атомом того чи іншого типу чи є проміжком між атомами, Поняття «гратка кристала» неприпустимо плутати з поняттям «структура кристала».
Таким чином головною властивістю кристалічних речовин є закономірне упорядковане розташування матеріальних частин у вузлах кристалічної гратки. Вузли гратки відповідають вершинам реальних кристалів; ряди, густо вкриті матеріальними частинками - ребрам кристалів; а площинні сітки з великою ретикулярною густиною – граням кристалів.
Під структурою кристаларозуміють конкретне розташування матеріальних частинок у просторі, симетрію та закони цього розташування. Структуру кристала досліджують по дифракції рентгенівських променів, дифракції електронів та нейтронів та іншими методами.
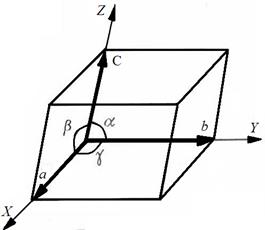 а, в, с – елементарні трансляція по осям Х, У, Z
α, β, γ – кути між кристалографічними осями
Рисунок 1.2 –Елементарний паралелепіпед
а, в, с – елементарні трансляція по осям Х, У, Z
α, β, γ – кути між кристалографічними осями
Рисунок 1.2 –Елементарний паралелепіпед
| Розташування атомів в кристалах однозначно описується його елементарною коміркою (рис.). Вона являє собою мінімальний об’єм кристалу , трансляцією якого вздовж трьох його ребер (осей координат), що виходять з однієї вершини (початок координат), на довжину цих ребер повністю відтворити структуру кристала. З метою опису кристалографічних багатогранників та структур застосовують метод кристалографічного індексування. Цей метод зручний для усіх систем координат – прямокутних і косокутних. Кристалографічне індексування дозволяє аналітично описувати геометричні елементи кристалів: точок (вузлів), прямих (рядів) та площин (площинних сіток). |
Для цього застосовують особливу символіку, однакову для всіх сингоній.
Символи вузлів. Просторова гратка – система вузлів, які знаходяться на кінцях векторів 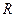
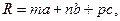
де 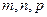 – три числа, які називаються індексами даного вузла.
– три числа, які називаються індексами даного вузла.
 Рисунок 1.3 . Символи вузлів, що розташовані у вершинах, у центрі граней та в центрі куба
Рисунок 1.3 . Символи вузлів, що розташовані у вершинах, у центрі граней та в центрі куба
|
Сукупність  що записана у квадратних дужках що записана у квадратних дужках 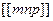 , називається символом вузла (рис.2.14). Числа в символах пишуться підряд без ком, читаються нарізно. Знак мінус пишуть над цифрою. , називається символом вузла (рис.2.14). Числа в символах пишуться підряд без ком, читаються нарізно. Знак мінус пишуть над цифрою.
|
Символи рядів (напрямків). Напрямок ряду, який проходить через початок координат, визначається двома точками: початком координат та будь-яким вузлом ряду. Для визначення символу ряду необхідно:
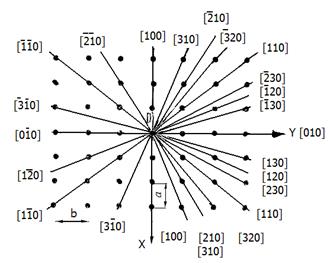 Рисунок 1.4 Символи деяких напрямків на площинній сітці
Рисунок 1.4 Символи деяких напрямків на площинній сітці
| 1 - перенести ряд паралельно самому собі на початок координат;
2 - визначити координати будь-якої точки цього напрямку, взявши за одиницю вимірювання період гратки;
3 - привести відношення одержаних величин до співвідношення трьох найменших чисел, котрі заключити у квадратні дужки 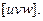 Осі координат мають символи:
Осі координат мають символи: 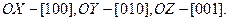 На рис.2.15 приведені символи декотрих напрямків в площинній сітці. На рис.2.15 приведені символи декотрих напрямків в площинній сітці.
|
Якщо необхідно позначити сукупність усіх кристалографічно-еквівалентних напрямків, то індекси заключають у ломані дужки  Так сукупність ребер куба позначається
Так сукупність ребер куба позначається  діагоналей граней -
діагоналей граней -  об`ємних діагоналей -
об`ємних діагоналей - 
Символи площин. В кристалографії прийнято характеризувати площини так званими індексами Міллера. Для визначення індексів площин необхідно:
- знайти відрізки, які відсікає дана площина на кристалографічних осях (за одиницю вимірювання приймають період гратки вздовж кожної осі);
- узяти обернені значення цих відрізків;
- привести відношення отриманих величин до співвідношення трьох цілих чисел. Ці три числа, що узяті у круглі дужки 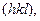 являють собою символ площини.
являють собою символ площини.
Символи  та (
та ( 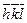 ) характеризують орієнтацію у просторі родин паралельних площин. Сукупність усіх непаралельних кристалографічно – еквівалентних площин, які мають однакову атомну будову, відзначаються символами, що беруть у фігурні дужки.Так, сукупність шести граней куба позначають символом
) характеризують орієнтацію у просторі родин паралельних площин. Сукупність усіх непаралельних кристалографічно – еквівалентних площин, які мають однакову атомну будову, відзначаються символами, що беруть у фігурні дужки.Так, сукупність шести граней куба позначають символом 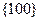 , восьми площин октаедра
, восьми площин октаедра 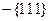 та дванадцяти площин ромбічного додекаедра
та дванадцяти площин ромбічного додекаедра 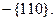

Рисунок 1.5 – Символи декотрих найважливіших вузлів, напрямків та площин в кубічній гратці
ПРАКТИЧНА ЧАСТИНА
1. Розв’язування поставленої задачи побудування вузлів, напрямків та площин за їх індексами необхідно проводити у зворотній послідовності визначення цих індексів.
- Обрати початок координат при цьому враховують, що позитивні (+) та негативні (-) напрямки осей відносно координат проводять таким чином:
- перша вісь (l або Х) – по горизонталі вперед (+) і назад (-);
- друга вісь (ll або Y) – по горизонталі праворуч (+) і ліворуч (-);
- третя вісь (lll або Z) – по вертикалі вгору (+) і вниз (-).
При виборі початку координат слід враховувати, що точка початку координат може бути суміщена з будь якою вершиною куба.
- Для побудови завданого напрямку з індексами [uvw] необхідно:
- обрати початок координат, зручний для побудови напрямку.;
- визначити точку закінчення напрямку, для цього необхідно всі три індекси напрямку поділити на найбільше значення одного з індексів напрямку. Отриманні три числа і будуть координатами точки;
- з’єднати початок координат із визначеною точку; це і буде завданий напрямок [uvw].
- Для побудови завданої площини з індексами (hkι) необхідно:
- вибрати початок координат для побудови завданої площини;
- записати величини обернені індексам площини (тобто 1/h, 1/k, 1/ι) – ці індекси і визначають відрізки, які відсікає площина на трьох координатних осях;
- з’єднати отримані три кінці відрізки прямими лініями – це і буде задана площина з індексами (hkι).
Практичне заняття виконується згідно із завданням кожним студентом окремо, перелік завдань наведений в додатку А, порядковий номер завдання відповідає порядковому номеру студента в студентському журналі.


ПРАКТИЧНЕ ЗАНЯТТЯ №2
Дата добавления: 2015-06-10; просмотров: 1177;
