Теория ошибок

Рассмотрим из-за чего в “правильно работающей” программе могут получаться не точные или совсем не правильные данные.

х – число;

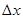– его ошибка;

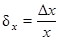– относительная ошибка.

В операциях сложения: 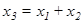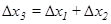_, то есть при сложении чисел происходит сложение их ошибок.

В операциях умножения: .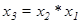

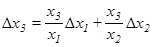При делении: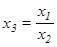

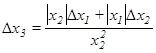
При возведении вещественного числа в целую и вещественную степень, мы получим разный результат, но в простом случае это расхождение будет в 9–10 знаке после запятой. B=5.7

A=5.7

B1=B**2=…

A1=A**2.=…

IF(A1.EQ.B1) THEN …

При сравнении переменных оператором IF, получим значение TRUE.

Однако если А1 и В1 являются результатом длительных вычислений (вычисление суммы, например) с использованием библиотечных программ ЭВМ для вычисления функций типа log, eхp, tg, sin, th, которые вычисляются с помощью разложения в бесконечный ряд, то окончательная ошибка будет возрастать. На некотором этапе может возникнуть ситуация, когда различие между переменными А1 и В1 обнаружится в 7 знаке после запятой. При этом оператор сравнения этих переменных не выполнится (результат сравнения будет равен FALSE). Если в алгоритме работы программы должна предусматриваться ситуация, когда А1 должна быть равна В1, то вместо IF(A1.EQ.B1) с ранее заданной точностью можно записать: IF(ABS(A1-B1).LT.1.E–6) THEN …