Эффект Джоуля — Томсона

Если идеальный газ адиабатически рас­ширяется и совершает при этом работу, то он охлаждается, так как работа в данном случае совершается за счет его внутрен­ней энергии (см. § 55). Подобный процесс, но с реальным газом — адиабатическое расширение реального газа с совершением внешними силами положительной рабо­ты — осуществили английские физики Дж. Джоуль (1818—1889) и У. Томсон (лорд Кельвин, 1824—1907).

Рассмотрим эффект Джоуля — Томсо­на. На рис. 93 представлена схема их опыта. В теплоизолированной трубке с по­ристой перегородкой находится два пор­шня, которые могут перемещаться без трения. Пусть сначала слева от перего­родки газ под поршнем 1 находится под давлением р₁, занимает объем V₁при тем­пературе Т₁, а справа газ отсутствует (по-

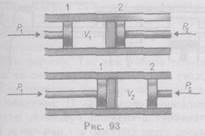
ршень 2 придвинут к перегородке). После прохождения газа через пористую перего­родку в правой части газ характеризуется параметрами р₂, V₂, Т₂. Давления р₁и р₂ поддерживаются постоянными (р₁>р₂).

Так как расширение газа происходит без теплообмена с окружающей средой (адиабатически), то на основании первого начала термодинамики

dQ=(U₂-U₁)+dA=0. (64.1)

Внешняя работа, совершаемая газом, со­стоит из положительной работы при дви­жении поршня 2 (A₂=p₂V₂) и отрицатель­ной при движении поршня 1 (A₁=p₁V₁), т.е. dA=A₂-А₁. Подставляя выраже­ния для работ в формулу (64.1), полу­чим

U₁+p₁V₁=U₂+p₂V₂. (64.2)

Таким образом, в опыте Джоуля — Томсона сохраняется (остается неизменной) ве­личина U+pV. Она является функцией состояния и называется энтальпией.

Ради простоты рассмотрим 1 моль га­за. Подставив в формулу (64.2) выраже­ние (63.3) и рассчитанные из уравнения Ван-дер-Ваальса (61.2) значения p₁V₁ и p₂V₂(символ «m» опять опускаем) и производя элементарные преобразова­ния, получим

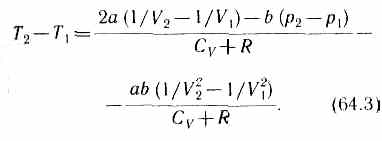
Из выражения (64.3) следует, что знак разности (T₂-T₁) зависит от того, какая из поправок Ван-дер-Ваальса играет боль­шую роль. Проанализируем данное выражение, сделав допущение, что p₂<<p₁

и V₂>>V₁:

1) a»0— не учитываем силы притя­жения между молекулами, а учитываем лишь размеры самих молекул. Тогда

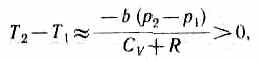
т. е. газ в данном случае нагревается;

2) b»0 - не учитываем размеров мо­лекул, а учитываем лишь силы притяже­ния между молекулами. Тогда

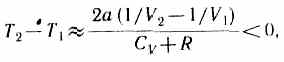
т. е. газ в данном случае охлаждается;

3) учитываем обе поправки. Подставив в выражение (64.3) вычисленное из урав­нения Ван-дер-Ваальса (61.2) значение p₁, имеем

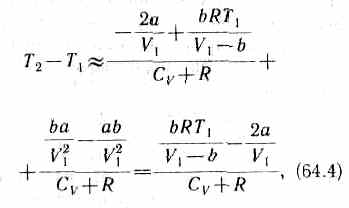
т. е. знак разности температур зависит от значений начального объема V₁и началь­ной температуры Т₁.

Изменение температуры реального га­за в результате его адиабатического рас­ширения, или, как говорят, адиабатиче­ского дросселирования— медленного про­хождения газа под действием перепада давления сквозь дроссель(например, по­ристую перегородку), называется эффек­том Джоуля — Томсона.Эффект Джоу­ля — Томсона принято называть положи­тельным,если газ в процессе дросселиро­вания охлаждается (DT<0), и отрица­тельным,если газ нагревается (DT>0).

В зависимости от условий дросселиро­вания для одного и того же газа эффект Джоуля — Томсона может быть как поло­жительным, так и отрицательным. Темпе­ратура, при которой (для данного давле­ния) происходит изменение знака эффек­та Джоуля — Томсона, называется температурой инверсии.

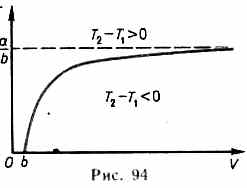
Ее зависимость от объема получим, приравняв выражение (64.4) нулю:

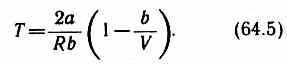
Кривая, определяемая уравнением (64.5),— кривая инверсии— приведена на рис. 94. Область выше этой кривой со­ответствует отрицательному эффекту Джоуля — Томсона, ниже — положитель­ному. Отметим, что при больших перепа­дах давления на дросселе температура газа изменяется значительно. Так, при дросселировании от 20 до 0,1 МПа и на­чальной температуре 17 °С воздух охлаж­дается на 35 °С.

Эффект Джоуля — Томсона обуслов­лен отклонением газа от идеальности. В самом деле, для моля идеального газа pV_m = RT, поэтому выражение (64.2) при­мет вид

C_VT₁+RT₁=C_VT₂ + RT₂, откуда следует, что T₁=T₂