Способ вспомогательных секущих плоскостей

Рассмотрим применение вспомогательных секущих плоскостей на примере построения линии пересечения сферы с конусом вращения (рис. 52).

Характерными точками проекций линии пересечения поверхностей являются точки Α, Β и С, D. Точки Α, Β находятся в пересечении очерковых образующих поверхностей, т.к. эти образующие расположены в одной секущей плоскости Ф, проходящей по плоскости симметрии поверхностей. Α и Β высшая и низшая точки линии пересечения. Точки С и D являются точками видимости горизонтальной проекции линии пересечения. Их построения выполнены в такой последовательности:

1) через центр сферы О проведена горизонтальная плоскость уровня Θ;

2) построена горизонтальная проекция окружности радиуса R¹, по которой плоскость Θ пересекает коническую поверхность; эта же плоскость пересекает сферу по экватору (окружности максимального радиуса);

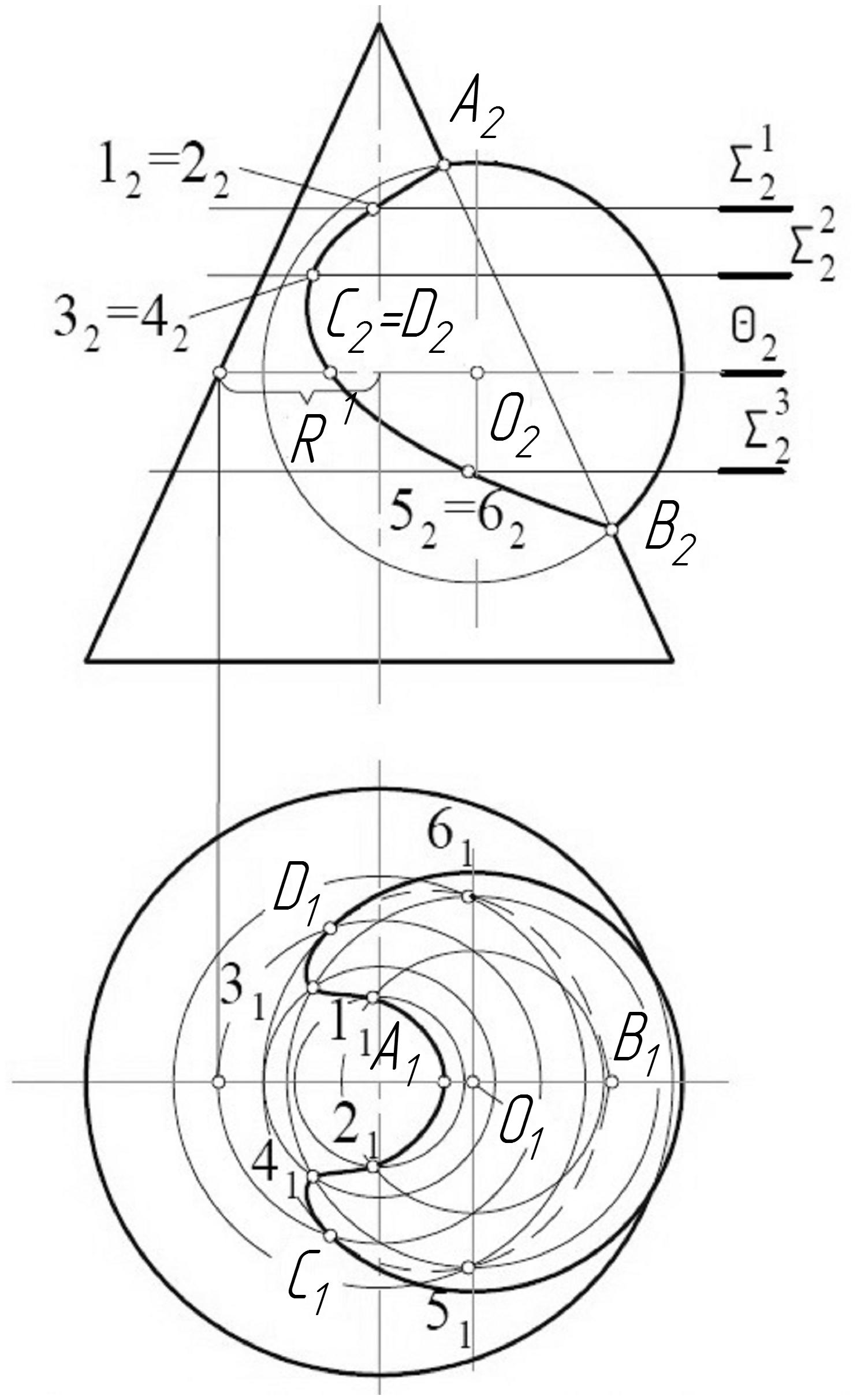
Рис. 52 Применение способа вспомогательных секущих плоскостей

3) построена горизонтальная проекция окружности радиуса R¹, по которой плоскость Θ пересекает коническую поверхность; эта же плоскость пересекает сферу по экватору (окружности максимального радиуса);

4) определены точки C₁, D₁ пересечения окружности радиуса R¹ с очерком сферы;

5) установлены фронтальные проекции точек С(С₂), D(D₂) из условия принадлежности их плоскости Θ.

Для построения промежуточных точек 1(1₁,1₂), 2(2₁,2₂), …, 6(6₁,6₂) линии пересечения заданных поверхностей используем плоскости 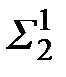, 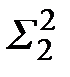и .

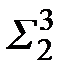Полученные точки соединим плавной кривой линией. Видимость линии пересечения определяется в каждой плоскости проекций.

Затем устанавливаются участки, видимые одновременно для обеих поверхностей. Так, при проецировании коническая поверхность своих точек не закрывает, а сфера закрывает точки, расположенные ниже горизонтального контура. Точки С и D, расположенные на горизонтальном очерке, отделяют видимую часть линии от невидимой. Невидимая часть показана штриховой линией. На П₂ проекции видимой части линии пересечения совпадает с проекцией невидимой, так как фронтальные очерки обеих поверхностей расположены в плоскости симметрии поверхностей.