Методом замены плоскостей проекций
Пусть ∆ABC – плоскость общего положения (рис. 33). В плоскости треугольника проведем горизонталь h, спроецируем горизонталь h в точку h4 на плоскость П4 (x14 ⊥ h1, П4 ⊥ h), построим новые проекции точек А4, В4, С4. Плоскость ∆ABC проецируется в прямую, проходящую через точки А4, В4, С4. Плоскость треугольника в системе (П1П4) является проецирующей плоскостью, она перпендикулярна П4. Треугольник АВС проецируется на П4 в отрезок В4С4.
Для нахождения натуральной величины ∆АВС введем плоскость проекций П5 параллельно плоскости треугольника и перпендикулярно П4. Новая ось x45 параллельна отрезку D4C4 (в противном случае ∆ABC и П5 пересекутся). Треугольник АВС проецируется на плоскость П5 в натуральную величину ΔА5В5С5 = ΔАВС.
Аналогично находится натуральная величина любой плоской фигуры.
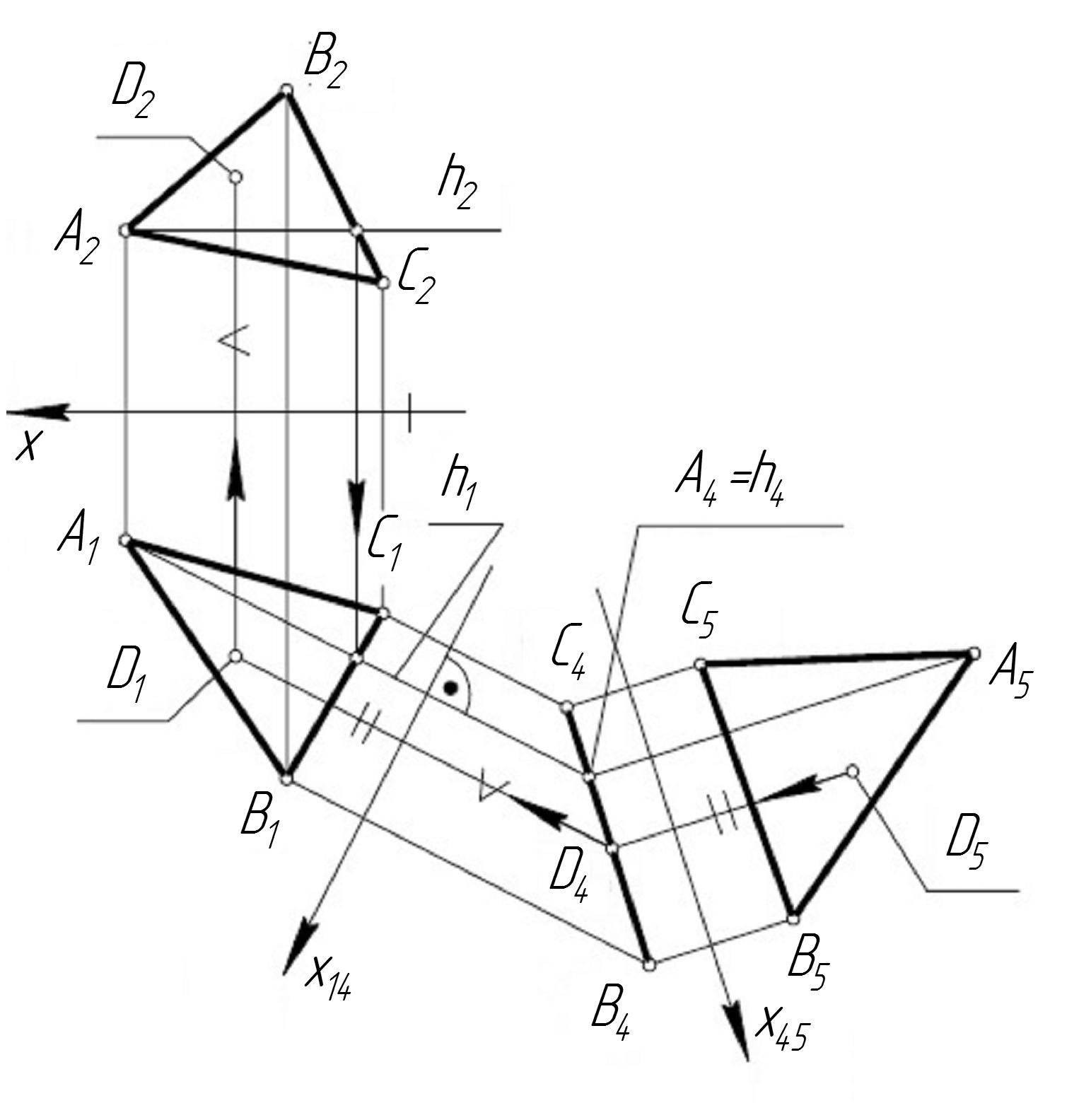
Рис. 33 Определение натуральной величины плоскости
Практическое задание № 3. Выполните чертеж двух пересекающихся плоскостей (формат А4).
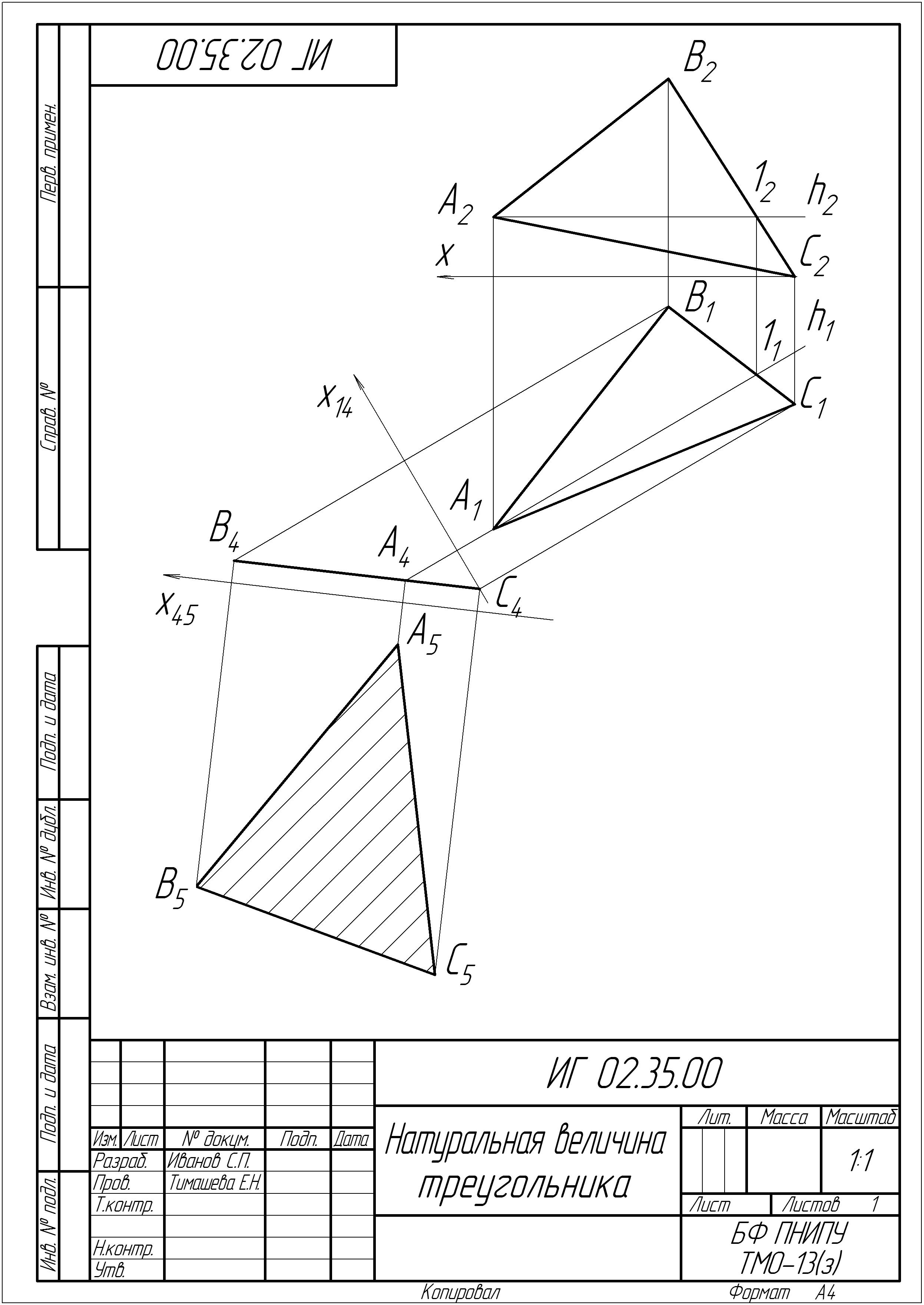
| Рис. 34 Образец выполнения практического задания № 3 |
Тема 4
Дата добавления: 2015-06-05; просмотров: 1782;
