Основанные на дисконтированных оценках
Система оценок экономической эффективности инвестиций делится на две группы:
Методы анализа эффективности инвестиций, основанные на дисконтированных (временных) оценках, включают:
- расчет чистой приведенной стоимости проекта (NPV);
- расчет индекса рентабельности инвестиций (PI);
- расчет внутренней нормы доходности (рентабельности) инвестиций (IRR);
- расчет дисконтированного срока окупаемости инвестиций (DPP);
- расчет минимума приведенных затрат.
Методы анализа эффективности инвестиций, основанные на простых (учетных) оценках:
- расчет срока окупаемости инвестиций (PP);
- расчет учетной нормы рентабельности (ARR);
- расчет коэффициента сравнительной экономической эффективности (Кэ).
Необходимость использования нескольких методов оценки вызвана тем, что результаты, получаемые с использованием различных методов, могут иметь противоречивый характер. Сравнивая результаты анализа эффективности инвестиций по различным методам, аналитик делает выводы о приемлемости того или иного проекта.
Расчет чистой приведенной стоимости (NPV)
Этот метод основан на использовании понятия чистого современного значения (Net Present Value).
Содержание метода состоит в том, что современное значение всех входных денежных потоков сравнивается с современным значением всех выходных потоков, обусловленных капитальными вложениями для реализации проекта. Разница между этими потоками – это и есть чистая приведенная стоимость (чистое современное значение) NPV.
Например, если в результате реализации проекта приведенная стоимость накопленных доходов составила 10 млн руб., а приведенная стоимость инвестиционных затрат – 8 млн руб., то чистая приведенная стоимость проекта равна 2 млн руб.
Таким образом, критерий NPV показывает современное значение чистого дохода (убытка) инвестора по проекту.
Алгоритм расчета:
Шаг 1. Определяется современное значение каждого денежного потока (входного и выходного).
Шаг 2. Суммируются все дисконтированные значения элементов денежных потоков, и определяется критерий NPV по формуле
NPV = Дисконтированные денежные доходы – Инвестиционные затраты,
или
NPV = ДП0 + ДП1/(1+r)1 + ДП2/(1+r)2+ ДПn/(1+r)n = ∑ ДПk/(1+r)k – IC,
где ДП − чистый денежный поток;
r − стоимость капитала инвестиционного проекта;
IC – инвестиции.
Применив дисконтирующий множитель, упростим расчет:
NPV = ДП0 + ДП1* FM2(r,1)+ ДП2* FM2(r,2)+…+ ДП k* FM2(r, k)– IC
Шаг 3. Производится принятие решения:
- если значение NPV > 0, проект является целесообразным, так как денежные доходы по проекту больше суммы предполагаемых расходов;
- если значение NPV < 0, проект является нецелесообразным, так как денежные расходы по проекту превышают доходы по нему;
- если значение NPV = 0, проект является безубыточным (доходы по проекту равны затратам по нему);
- если производится принятие решение по ряду альтернативных проектов, принимается тот из них, который имеет большее значение NPV, если только оно положительное.
Пример 4.1. Компания планирует приобрести новое оборудование стоимостью 7000 тыс. руб. и сроком эксплуатации 5 лет. Компания будет получать дополнительный денежный приток в размере 2500 тыс. руб. ежегодно. Известно, что на третьем году эксплуатации оборудованию потребуется плановый ремонт стоимостью 300 тыс. руб. Необходимо обосновать целесообразность приобретения оборудования, если стоимость капитала по проекту составляет 20%.
Представим условия задачи в виде исходных данных (табл. 4.1).
Таблица 4.1
Исходные данные для расчета
| Показатель | Величина |
| Стоимость оборудования, тыс. руб. | |
| Срок эксплуатации, лет | |
| Стоимость ремонта на 3-м году, тыс. руб. | |
| Дополнительный входной денежный поток, тыс. руб. | |
| Показатель дисконта, % |
Расчет произведем с помощью таблицы 4.2.
Таблица 4.2
Расчет чистой приведенной стоимости
| Наименование денежного потока | Годы | Денежный поток, тыс. руб. | Финансовый множитель | Настоящее значение денег, тыс. руб. |
| 5 = 3*4 | ||||
| Исходная инвестиция | Сейчас | -7000 | -7000 | |
| Входной денежный поток | (1-5) | FM4 (20%, 5) = = 2,991 | 7477,5 | |
| Ремонт оборудования | -300 | FM2 (20%, 3) = = 0,579 | -173,7 | |
| Современное чистое значение (NPV) | 303,8 |
В результате расчетов мы получили значение NPV = 303,8 тыс. руб. > 0, и поэтому, с финансовой точки зрения, проект следует принять.
Очевидно, что значение критерия NPV является функцией от показателя дисконта, т.е. при изменении размера ставки дисконта (цены капитала инвестиционного проекта) будет изменяться значение критерия NPV.
Можно сказать, что уровень NPV характеризует запас финансовой прочности по проекту. Если значение критерия NPV достаточно высокое для данного проекта, то незначительные колебания ставки дисконта во время его реализации не принесут инвестору чрезмерных финансовых потерь и проект будет доходным.
Если же значение критерия NPV низкое, то колебания показателя дисконта, например повышение процентных ставок по коммерческим кредитам, может принести инвестору значительные финансовые затруднения и проект из доходного может превратиться в убыточный.
Подтвердим справедливость этих утверждений примером.
Повысим процентную ставку в рассматриваемом примере до 24% годовых и рассчитаем значение критерия NPV (табл. 4.3).
Таблица 4.3
Расчет чистой приведенной стоимости
| Наименование денежного потока | Годы | Денежный поток, тыс. руб. | Финансовый множитель | Настоящее значение денег, тыс. руб. |
| 5 = 3*4 | ||||
| Исходная инвестиция | Сейчас | -7000 | -7000 | |
| Входной денежный поток | (1-5) | FM4 (24%, 5) = 2,745 | 6862,5 | |
| Ремонт оборудования | -300 | FM2 (24%, 3) = 0,524 | -157,2 | |
| Современное чистое значение (NPV) | -294,7 |
Расчет показывает, что при r = 24% критерий NPV имеет отрицательное значение. Это свидетельствует о том, что исходная инвестиция не окупается, т.е. положительные денежные потоки, которые генерируются этой инвестицией, не достаточны для компенсации с учетом стоимости денег во времени, исходной суммы капитальных вложений.
Общий вывод таков: при увеличении нормы доходности инвестиций (стоимости капитала инвестиционного проекта) значение критерия NPV уменьшается.
Достоинством показателя NPV является то, что он обладает свойством аддитивности, т.е. при рассмотрении взаимодополняющих инвестиционных проектов А и Б доход, получаемый инвесторами, будет равен сумме доходов каждого из проектов в отдельности:
NPVA+Б = NPVA + NPVБ.
Для полноты представления информации, необходимой для расчета NPV, приведем типичные денежные потоки.
Типичные входные денежные потоки:
- дополнительный объем продаж и увеличение цены товара;
- уменьшение валовых издержек (снижение себестоимости товаров);
- остаточное значение стоимости оборудования в конце последнего года инвестиционного проекта (так как оборудование может быть продано или использовано для другого проекта);
- высвобождение оборотных средств в конце последнего года инвестиционного проекта (закрытие счетов дебиторов, продажа остатков товарно-материальных запасов, продажа акций и облигаций других предприятий).
Типичные выходные потоки:
- начальные инвестиции в первый год(ы) инвестиционного проекта;
- увеличение потребностей в оборотных средствах в первый год(ы) инвестиционного проекта (увеличение счетов дебиторов для привлечения новых клиентов, приобретение сырья и комплектующих для начала производства);
- ремонт и техническое обслуживание оборудования;
- дополнительные непроизводственные издержки (социальные, экологические и т. п.).
Расчет индекса рентабельности инвестиций (PI)
Индекс рентабельности инвестиций (Profitability Index) – относительный показатель, который рассчитывается как отношение дисконтированного дохода к инвестиционным затратам. Характеризует, каким образом доходы инвестиционного проекта покрывают затраты по нему. Рассчитывается по формуле:
PI = ∑ ДПk/(1+r)k / IC.
Решение по этому критерию принимается следующим образом:
- если PI ≥ 1, то проект принимается, так как доходы по инвестиционному проекту превышают затраты по нему;
- если PI < 1, то проект отклоняется, так как доходы по инвестиционному проекту меньше предполагаемых затрат.
Индекс рентабельности является относительным показателем. Благодаря этому, он очень удобен при выборе одного проекта из ряда альтернативных, имеющих приблизительно одинаковые NPV, либо при комплектовании портфеля инвестиций с максимальным суммарным значением NPV.
Рассчитаем для примера 4.1 индекс рентабельности инвестиций. В случае когда процентная ставка r = 20%, индекс рентабельности инвестиций составит
PI = 7477,5 / (7000+173,7) = 1,042, или 104,2%.
В случае когда процентная ставка r = 24%, индекс рентабельности инвестиций составит
PI = 6862,5 / (7000+157,2) = 0,959, или 95,9%.
Итак, при увеличении цены капитала проекта его рентабельность снижается.
Расчет внутренней нормы рентабельности (IRR)
Внутренняя норма рентабельности (доходности)(Internal Rate of Return) − это такое значение показателя дисконта, при котором современное значение расходов по проекту равно современному значению доходов по нему.
Таким образом, внутренняя норма доходности – это такая процентная ставка, при которой чистая приведенная стоимость проекта равна нулю:
IRR = r,при которой NPV = 0.
Экономический смысл внутренней нормы доходности IRR состоит в том, что этот показатель характеризует максимально допустимый уровень расходов по инвестиционному проекту. IRR является критическим, пороговым показателем: если стоимость капитала выше значения IRR, то «мощности» проекта недостаточно, чтобы обеспечить необходимый возврат и отдачу денег, и, следовательно, проект следует отклонить.
Схема принятия решения на основе метода внутренней нормы прибыльности имеет следующий вид:
- если значение IRR выше или равно стоимости капитала, то проект принимается;
- если значение IRR меньше стоимости капитала, то проект отклоняется.
Рассмотрим методику расчета IRR на нашем примере.
Пример 4.2.Ранее, в примере 4.1, мы определили, что при цене капитала проекта r = 20% приведенная норма доходности NPV составляет 303,8 тыс. руб., а при r = 24% приведенная норма доходности NPV составляет -294,7 тыс. руб.
Представим графическую интерпретацию решения (рис. 4.1).
Созданный нами график – это так называемый NPV-профиль. Для нас представляет интерес точка пересечения NPV-профиля с осью абсцисс. Эта точка rx характеризует такое значение цены капитала проекта r, при которой NPV проекта равно нулю.
|
|
|
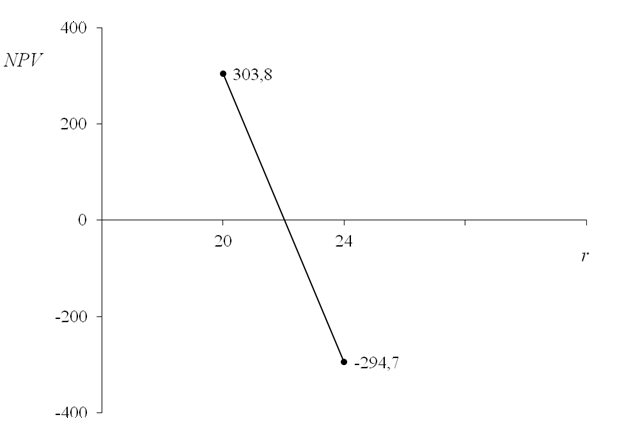
Рис. 4.1. Вид NPV-профиля
Таким образом, точка пересечения NPV-профиля с осью абсцисс – это и есть внутренняя норма доходности проекта IRR. Левее этой точки, т.е. когда цена капитала проекта меньше значения IRR, проект является доходным. Если же цена капитала проекта превышает значение IRR (на графике находится правее), проект входит в зону убытков.
В общем случае уравнение для определения IRR не может быть решено в конечном виде, хотя существуют ряд частных случаев, когда это возможно.
Обычно для нахождения критерия IRR используют формулу линейной интерполяции:
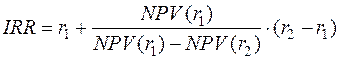 ;
;
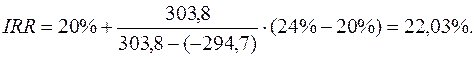
Итак, если цена капитала проекта будет меньше 22,03%, то инвестиционный проект является прибыльным. Если же цена капитала инвестиционного проекта будет выше 22,03%, проект убыточен.
Расчет критерия IRR будет тем более точным, чем ближе точки r1 и r2 расположены друг к другу. При этом функция, т.е. NPV, должна изменять знак: если при заданном r1 функция NPV имеет положительный знак, то при r2 значение NPV должно быть отрицательным.
Существуют более точные методы определения IRR, которые предполагают использование специального финансового калькулятора или электронного процессора EXCEL.
Найти значение IRR можно и другим способом.
Пример 4.3. На покупку оборудования требуется 5700 тыс. руб. В течение 5 лет за счет экономии ручного труда компания планирует получать дополнительный годовой доход в размере 1500 тыс. руб. Остаточная стоимость оборудования равна нулю. Надо найти IRR.
Найдем значение IRR, используя формулу современного значения аннуитета:
PVA = A · FM4(r, n),
т.е. 5700 = 1500 · FM4(r, 5).
Найдем отношение требуемого значения инвестиции к ежегодному притоку денег, которое будет совпадать с множителем какого-либо (пока неизвестного) коэффициента дисконтирования:
FM4(r, 5) = 5700 / 1500 = 3,8.
С помощью финансовой таблицы находим, что для n = 5 показатель дисконта составляет 10%. Это и есть искомое значение IRR.
Произведем проверку правильности расчетов (табл. 4.4).
Таблица 4.4
Проверка правильности расчетов
| Наименование денежного потока | Годы | Денежный поток, тыс. руб. | Финансовый множитель | Настоящее значение денег, тыс. руб. |
| 5 = 3*4 | ||||
| Исходная инвестиция | Сейчас | -5700 | -5700 | |
| Годовая экономия | (1-5) | FM4 (10%, 5) = 3,8 | ||
| Современное чистое значение (NPV) |
Таким образом, мы подтвердили, что IRR = 10%. Успех решения был обеспечен совпадением отношения исходной суммы инвестиций к величине денежного потока с конкретным значением множителя дисконта.
Использование IRR в качестве критерия оценки экономической эффективности инвестиций имеет как положительные, так и отрицательные стороны.
Преимущества использования IRR заключаются в следующем:
- IRR прост для понимания: он показывает предельно допустимый уровень расходов по проекту;
- IRR характеризует запас «финансовой прочности» проекта, т.е чем меньше цена капитала инвестиционного проекта по сравнению с его внутренней нормой доходности, тем более привлекательным и прибыльным будет проект для инвестора;
- расчет IRR не сопряжен со значительными трудностями.
Недостатки использования IRR:
- множественность значений − результаты расчета внутренней нормы рентабельности прямо зависят от того, сколько раз меняется знак у соответствующих денежных потоковинвестиционного проекта;
- отсутствие свойства аддитивности (IRR A + B ≠ IRRA + IRRB);
- ошибочность ранжирования взаимоисключающих проектов по критерию IRR.
Совместное использование методов NPV и IRR рекомендуется осуществлять следующим образом.
При оценке альтернативных проектов следует производить их ранжирование для выбора по максимуму NPV. Роль IRR в основном, сводится к оценке пределов, в которых может находиться норма дисконта (при высокой неопределенности цены денег это весьма существенно).
Расчет дисконтированного периода окупаемости (DPP)
Срок окупаемости инвестиционного проекта представляет собой период времени с момента начала финансирования инвестиционного проекта до момента, когда разность между накопленной суммой доходов и амортизационными отчислениями и затратами по проекту принимает положительное значение.
Иными словами, это – период (измеряемый в месяцах, кварталах или годах), начиная с которого первоначальные вложения и другие затраты, связанные с инвестиционным проектом, покрываются суммарными результатами его осуществления.
Метод дисконтированного периода окупаемости(Discounted Payback Period) используется для нахождения уточненного срока окупаемости инвестиционного проекта с учетом временной оценки денежных потоков по нему.
Рассмотрим применение метода дисконтированного срока окупаемости на конкретном примере анализа двух взаимоисключающих друг друга проектов.
Пример 4.4. Инвестор должен сделать выбор между двумя проектами А и Б, предполагающими одинаковый объем инвестиций − 1000 тыс. руб. по сроку окупаемости. Оба проекта рассчитаны на четыре года.
Проект А генерирует следующие денежные потоки: 500 тыс. руб. в первый год реализации, 400 тыс. руб. – во второй год, 300 тыс. руб. – в третий, 200 тыс. руб. – в четвертый.
Денежные потоки проекта Б: 200, 300, 400, 500 тыс. руб. соответственно.
Стоимость капитала проекта оценена на уровне 10% годовых.
Расчет дисконтированного срока окупаемости осуществляется с помощью таблицы 4.5.
Таблица 4.5
Расчет дисконтированного срока окупаемости проекта А
| Год | Денежный поток, тыс. руб. | Финансовый множитель | Дисконтированный денежный поток | Накопленный денежный поток, тыс. руб. |
| -1000 | -1000 | -1000 | ||
| 0,909 | 454,5 | -545,5 | ||
| 0,826 | 330,4 | -215,1 | ||
| 0,751 | 225,3 | 10,2 | ||
| 0,683 | 136,6 | 146,8 | ||
| Современное чистое значение (NPV) | 146,8 |
Последняя колонка таблицы 4.5 содержит сведения о непокрытой части исходной инвестиции. С течением времени величина непокрытой части уменьшается. Так, к концу второго года непокрытыми остаются 215 тыс. руб. В третий год реализации проекта первоначальные инвестиции полностью покрываются накопленными доходами.
Таким образом, период окупаемости инвестиционного проекта А составляет 2 полных года и какую-то часть от третьего года.
Формула для расчета будет выглядеть следующим образом:
DPРА = 2 + 215/225 = 2,96 года.
Для того чтобы узнать, сколько месяцев составляет дробная часть года, необходимо дробь домножить на 12:
DPРА = 2 + 215/225 · 12 = 2 года и 11,5 месяцев.
Аналогично расчет дисконтированного периода окупаемости имеют следующий вид (табл. 4.6).
Таблица 4.6
Расчет дисконтированного срока окупаемости проекта Б
| Год | Денежный поток, тыс. руб. | Финансовый множитель | Дисконтированный денежный поток | Накопленный денежный поток, тыс. руб. |
| -1000 | -1000 | -1000 | ||
| 0,909 | 181,8 | -818,2 | ||
| 0,826 | 247,8 | -570,4 | ||
| 0,751 | 300,4 | -270,0 | ||
| 0,683 | 341,5 | 71,5 | ||
| Современное чистое значение (NPV) | 71,5 |
DPРВ = 3 + 270/341 = 3,79,
или
DPРВ = 3 + 270/341 · 12 = 3 года и 9,5 месяцев.
На основе полученных результатов можно сделать вывод о том, что проект А предпочтительнее для инвестора, поскольку он имеет меньший дисконтированный период окупаемости.
Инвестору уместно в своих выводах о целесообразности финансирования проекта руководствоваться и критерием NPV. Более высокое значение этого критерия также имеет проект А (146,8 тыс. руб.) по сравнению с проектом Б (71,5 тыс. руб.). Таким образом, оба критерия говорят о приоритетности проекта А.
Достоинствами этого метода являются простота расчетов и удобство в понимании.
Существенным недостатком метода дисконтированного периода окупаемости является то, что он учитывает только начальные денежные потоки, именно те потоки, которые укладываются в период окупаемости. Все последующие денежные потоки во внимание не принимаются.
Так, если бы в рамках второго проекта в последний год поток составил, например, 1000 тыс. руб., то результат расчета дисконтированного периода окупаемости не изменился бы, хотя совершенно очевидно, что проект станет в этом случае гораздо более привлекательным.
Дата добавления: 2015-06-05; просмотров: 1834;
