ЗАДАЧИ 21-28

Построение шатунных кривых. Для их построения следует брать 6 равноотстоящих положений ведущего звена механизма.

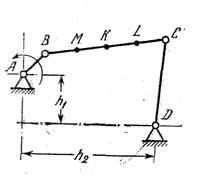
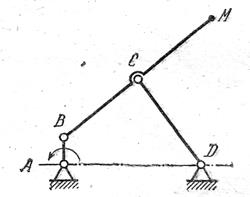
Задача 21. Вычертить шатунные кривые, описываемые точками М, К, L коромыслового механизма. Исходные данные: АВ=50 мм, ВС=200 мм, CD=140 мм, h₁=80 мм, h₂=220 мм, ВМ=МК=КL=0,25ВС.

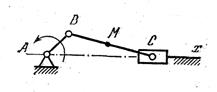
Задача 22. Вычертить шатунную кривую, описываемую точкой М кривошипно-ползунного механизма. Исходные данные: АВ=50 мм, ВС=150 мм, ВМ=75 мм.

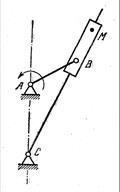
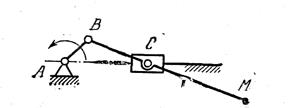
Задача 23. Вычертить шатунную кривую, описываемую точкой М механизма Витворта. Исходные данные: АВ=60 мм, АС=80 мм, ВМ=40 мм.

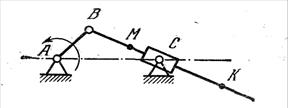
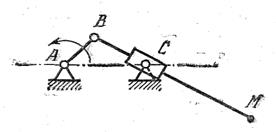
Задача 24. Вычертить шатунные кривые, описываемые точками М и К кривошипного механизма с качающимся ползуном. Исходные данные: АВ=50 мм, АС=140 мм, ВМ=60 мм, ВК=200 мм.

Задача 25. Вычертить шатунную кривую, описываемую точкой М кривошипно-ползунного механизма. Исходные данные: АВ=10 мм, ВС=30 мм, ВМ=96 мм.

Задача 26. Вычертить шатунную кривую, описываемую точкой М кривошипного механизма с качающимся ползуном. Исходные данные: АВ=20 мм, АС=30 мм, ВМ=119 мм.

Задача 27. Вычертить шатунную кривую, описываемую точкой М механизма противовращательной рукоятки Чебышева. Исходные данные: АВ=6,8 мм, ВС=СD=СМ=50 мм, AD=70,45 мм.

Задача 28. По условию Задачи 21 определить угол β размаха коромысла СD.

§3. Планы скоростей и ускорений механизма строятся после решения задачи о его положении, причем построение планов проводится для отдельных групп Ассура, которые образовали механизм. Вначале строится план скоростей (ускорений) группы, которая присоединена элементами своих внешних кинематических пар к ведущему звену и стойке, затем строятся планы скоростей (ускорений) второй и т.д. групп, взятых в той же последовательности, в какой они присоединяются при образовании механизма. Эта последовательность обозначена в формуле строения механизма (см. п. 1.4, формула (1.9)).

Рассмотрим кинематику ведущего звена. Ведущее звено изображено в масштабе 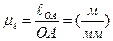(рисунок 2.3, а). Скорость точки А будет вычисляться по формуле

υ_А = ω₁ ℓ_ОА = (м/с).

Вектор скорости 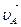^ОА и направлен в сторону ω₁ (рисунок 2.3,б).

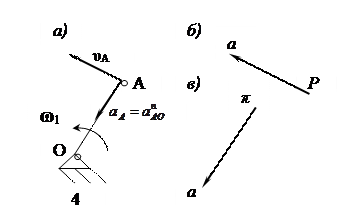
а – схема ведущего звена; б – план скоростей; в - план ускорений

Рисунок 2.3. - Кинематический анализ ведущего звена

Угловая скорость ведущего звена – величина постоянная (ω₁=const). Поэтому, полное ускорение 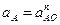(ε₁=0, 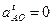). Тогда

.

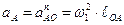Вектор 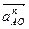||ОА и направлен к центру вращения (рисунок 2.3, в).

Примечание. Р – полюс (начало построения) плана скоростей; π – полюс плана ускорений.

На плане скоростей скорость точки А изображается отрезком (Ра) (рисунок 2.3, б), а нормальное ускорение этой точки - отрезком (πа) (рисунок 2.3, в). Масштабами планов скоростей и ускорений соответственно будут

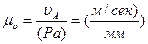, (2.2, а)

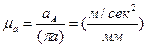, (2.2, б)

а масштабами планов аналогов скоростей и ускорений будут

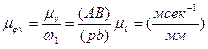, (2.3, а)

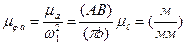. (2.3, б)

В некоторых случаях полезно строить повернутые планы скоростей, т.е. такие, у которых все векторы скоростей повернуты в одну и ту же сторону на 90° относительно их действительных направлений. Эти планы отличаются от обычных (не повернутых) большей точностью построения и, кроме того, удобны в качестве рычага Жуковского для определения уравновешивающей или приведенной силы.

Последовательность решения задачи на построение планов скоростей и ускорений (предполагается, что задача о положении решена и, следовательно, предварительно выяснено строение механизма и назначено ведущее звено):

1) Выполняется структурный анализ и записывается формула строения механизма.

2) Определяют скорость и ускорение ведущего звена. Высчитывают масштабы скорости и ускорения.

3) Строят план скоростей группы Ассура, непосредственно присоединенной к ведущему звену и стойке.

4) Строят план ускорений той же группы.

5) Переходят к построению планов скоростей и ускорений следующей присоединенной группы Ассура и так продолжают до тех пор, пока не будут построены планы скоростей и ускорений всех групп механизма.

Задачу кинематического анализа следует считать решенной, если для каждого звена механизма будут известны положения, скорости и ускорения двух его точек или станут известными положение, скорость и ускорение одной точки и угловая координата, угловая скорость и угловое ускорение самого звена.

Решим несколько примеров на построение планов скоростей и ускорений.

Пример 2.Дан механизм соломонабивателя (рисунок 2.4, а).

Известно: угловая скорость входного звена w₁ = 6 (рад/с); длины звеньев ℓ_О1А = 0,25 (м), ℓ_АВ =1,2 (м), ℓ_ВО3 = 0,6 (м), ℓ_АС = 0,2ℓ_АВ; расстояния между опорами ℓ_Х =ℓ_О1О3 =1,4 (м), ℓ_У =0,20 (м) 1,2; расстояния до центров масс АS₂ = 0,4 AB, O₃S₃ = 0,6 O₃B.

Определить: скорость и ускорение точки С, а также угловую скорость w₂ и угловое ускорение ξ₂ звена 2.

Решение. Строение механизма. Число подвижных звеньев n=3, число кинематических пар V класса р₅=4, степень подвижности W=1. Данный механизм состоит из одной группы Ассура II класса 1-го вида (звенья 2, 3) и ведущего звена 0₁Асо стойкой 4. Формула строения .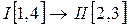

Построение схемы механизма. Рассчитываем масштабный коэффициент длины по формуле (2.1)

,

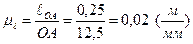где ОА=12,5 мм (выбирается произвольно). Тогда

, ,

, , .

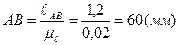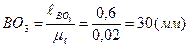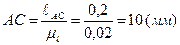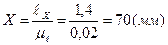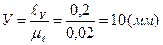Из произвольно выбранной на поле чертежа точки О₁ проводим окружность радиусом R=OA=12,5 мм (траектория движения точки А). Откладываем расстояния Х=70 мм и У=10 мм и отмечаем стойку О₃. Согласно заданию откладываем угол φ=30^о и отмечаем точку А. Далее, из точки А проводим окружность радиусом R=АВ (60 мм), а из точки О₃ проводим окружность радиусом R=ВО₃ (30 мм). Пересечение этих дуг есть искомая точка В (рисунок 2.4,а). Для нахождения точки С откладываем угол 130^о и отмеряем отрезок АС=10 мм.

Построение плана скоростей. Рассмотрим ведущее звено. Точка А вращается против часовой стрелке относительно точки О₁. Поэтому вектор скорости точки A 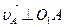и направлен в сторону вращения w₁. Величина скорости u_а определиться по формуле

.

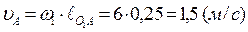Масштаб плана скоростей равен:

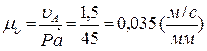. (2.4)

Начинаем построение плана скоростей. Выбираем в качестве полюса плана скоростей точку Р(рисунок 2.4, б) и откладываем от нее отрезок [Ра]= 45 мм перпендикулярно кривошипу О₁Ав сторонуw₁.

Рассмотрим структурную группу II класса 1 вида (звенья 2-3). Движение точки Вразложим на переносное поступательное со скоростями точек Аи О_з и относительное вращательное соответственно вокруг точек Аи О₃.Тогда векторные уравнения для скорости точки Вбудут иметь вид:

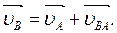
(2.5)

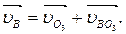
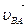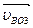В уравнении (2.5) все скорости известны по направлению: ^ВА, ^В0₃.

Величины скоростей u_ВА и u_ВО3найдем построением плана скоростей.

Продолжаем построение плана скоростей. Через точку авектора 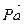проводим прямую, перпендикулярную звену ВАпроизвольной длины, а из полюса Рпроводим перпендикуляр к оси звена О₃Втакже произвольной длины. На пересечении получаем искомую точку в.

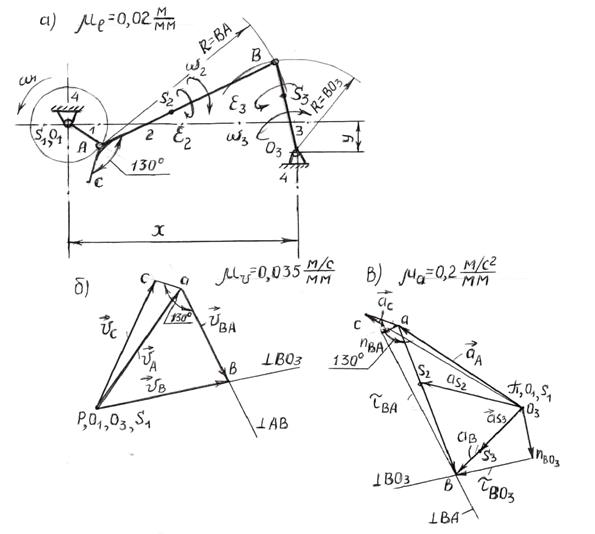
Рисунок 2.4. - Схема шарнирного четырехзвенного механизма

соломонабивателя, его планы скоростейи ускорений

Скорость точки «С»определяем по правилу подобия:

1. если на схеме механизма имеется жесткий треугольник (ΔАВС), то на плане скоростей (ускорений) будет подобный треугольник (Δавс), причем порядок букв на схеме механизма будет совпадать с порядком букв на плане скоростей или ускорений (обход контура);

2. если точка находится на звене и делит его на пропорциональные отрезки, то данная точка на плане скоростей(ускорений) будет находиться на соответствующем векторе и делить его на равнозначные пропорциональные отрезки;

3. если точка находится на продолжении звена, то на плане скоростей (ускорений) она будет находиться на продолжении соответствующего вектора, причем порядок букв на схеме механизма будет совпадать с порядком букв на плане скоростей или ускорений.

Воспользуемся п.1 из правила подобия. Для этого на стороне bа строим треугольник Δвac подобный треугольнику ΔBAC. Соединяем точку «с» с полюсом Р.(Можно точку «с» определить следующим образом. От вектора 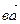отложить по часовой стрелке угол 130^о и на нем отложить отрезок 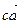, длина которого определиться из пропорции ).

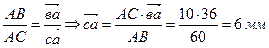После построения плана рассчитываем действительные значения скоростей:

,

,

.

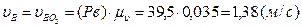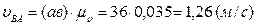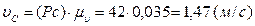Угловые скорости 2-го и 3-го звеньев определим по формулам:

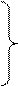
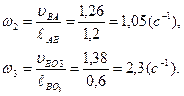(2.6)

Для определения направлений угловых скоростей необходимо вектора линейных скоростей 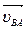, 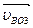перенести (мысленно) в точку Вна схеме механизма и наблюдать направление поворота точки В относительно точек А и О₃. При этом получились направления: w₂ и w₃ по часовой стрелке.

Построение плана ускорений. Рассмотрим ведущее звено. Полное ускорение точки Аявляется нормальным (а_А = аⁿ_АО), так как w₁ = const = 6 (рад/с). Поэтому

.

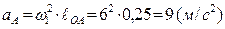Вычисляем масштаб плана ускорений

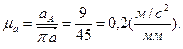
Начинаем построение плана ускорений. Из точки π,принимаемой за полюс (рисунок 2.4, в), проводим отрезок [πа] = 45 мм параллельно звену О₁А к центру вращения (к точке О₁).

Рассмотрим структурную группу II класса 1 вида (звенья 2-3). При определении ускорения внутреннего шарнира (точки В) следует помнить, что в группах Ассура II класса 1-го вида всегда известны ускорения внешних пар. В нашем случае

a_О3=0, а_А = 9 (м/с²).

Для определения ускорения а_Вточки В, как и для определения скорости υ_В точки В, рассматриваем ее движение, как сложное, состоящее из переносного поступательного с ускорениями а_Аи а_О3 и относительного вращательного вокруг точек Аи О₃. Тогда векторные уравнения для определения ускорения точки Вбудут следующими:

,

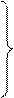
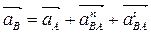(2.7)

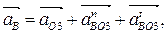
где а_Оз = 0.

В этих уравнениях известны направления всех векторов:

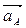|| АО₁; 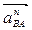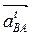|| ВА; ^ВА, 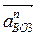|| ВО₃; 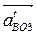^ BO₃.

Величины нормальных ускорений всегда можно найти, если построен план скоростей:

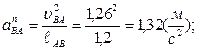
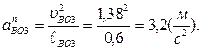
Тангенциальные ускорения в выражении (2.7) найдем построением плана ускорений.

Вычисляем длины векторов 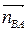и 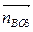, изображающие на плане ускорений ускорения 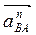и

.

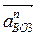
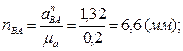
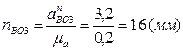Продолжаем построение плана ускорений. Через точку авектора 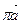проводим вектор 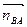= 6,6 (мм) параллельно звену АВв направлении от точки В к точке А. Из конца вектора 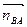проводим прямую, перпендикулярную звену АВпроизвольной длины. Из полюса πпроводим вектор 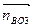= 16 (мм) параллельно звену ВО₃в направлении от точки В к точке О₃. Через конец вектора 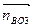- перпендикуляр к оси звена ВО₃ произвольной длиной. Точка «в»пересечения двух прямых определит длины векторов 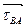и . 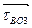Модули ускорени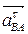й и 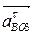, равны:

,

.

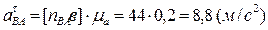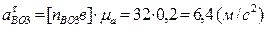Угловые ускорения ε₂ и ε₃ определяем через тангенциальные:

, .

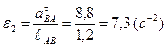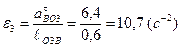Ускорения центров масс звеньев 2 и 3 определяем по правилу подобия. Согласно заданию имеем:

[aS₂] = 0,4 [aв] = (мм), [πS₃] = 0,6 [πв] = (мм).

Соединив полученные точки с полюсом π, получим вектора ускорений центров масс. Значения этих ускорений равны:

а_S2 = [πS₂] ∙ µ_а = 38 · 0,2 = 7,6 (м/с²),

a_S3 = [πS₃] ∙ µ_а = 18 · 0,2 = 3,6(м/с²).

Ускорение точки Сопределяем также по правилу подобия, п.1. Для этого на стороне bастроим треугольник Δвacподобный треугольнику ΔBAC. Соединяем точку «с» с полюсом π. Действительное значение ускорения определиться

а_C = µ_а· [π_C] = 53 ·0,2 = 10,6 (м/с²).

Пример 3. Определить скорость и ускорение поршня В, угловые скорость и ускорение 2-го звена, скорость и ускорение точки S₂ (рисунок 2.5). Задачу решить методом планов.

Исходные данные. Длины звеньев: кривошипа ℓ_ОА=0,3 м, шатуна ℓ_АВ=0,8 м. Угловая скорость кривошипа ω₁=30 с^-1. Расстояние до центра масс АS₂=0,5АВ. Угол φ=60⁰.

Определить.υ_В, а_В, ω₂, ε₂, υ_S2, а_S2.

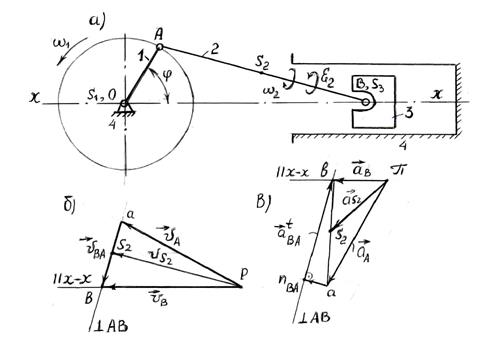
а – схема механизма; б – план скоростей; в – план ускорений

Рисунок 2.5. - Кинематический анализ кривошипно-ползунного

механизма (ДВС)

Решение. Строение механизма. Число подвижных звеньев n=3, число кинематических пар V класса р₅=4, степень подвижности W=1. Механизм образован присоединением к ведущему звену ОА и стойке 4 структурной группы II класса 2 вида, состоящей из звеньев 2 и 3. Формула строения .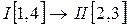

Построение схемы механизма. Рассчитываем масштабный коэффициент длины по формуле (2.1)

,

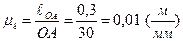где ОА=30 мм (выбирается произвольно). Тогда

.

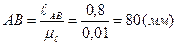Из произвольно выбранной на поле чертежа точки О проводим окружность радиусом R=OA=30 мм (траектория движения точки А). Согласно заданию откладываем угол φ=60^о и отмечаем точку А. Далее, из точки А проводим окружность радиусом R=АВ (80 мм) до пересечения с линией х-х. Отмечаем точку В (рисунок 2.5,а).

Построение плана скоростей. Рассмотрим ведущее звено. Точка А вращается против часовой стрелке относительно точки О(рисунок 2.5, а). Поэтому вектор скорости точки А 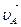^ОА и направлен в сторону вращения w₁. Величина скорости u_В определиться по формуле

.

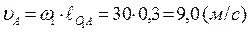Масштаб плана скоростей равен:

.

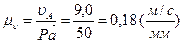Начинаем построение плана скоростей. Выбираем в качестве полюса плана скоростей точку Р(рисунок 2.5, б) и откладываем от нее отрезок [Ра]= 50 мм перпендикулярно кривошипу ОАв сторонуw₁.

Рассмотрим структурную группу II класса 2 вида (звенья 2-3). Скорость точки В определим из построения векторных уравнений

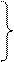
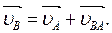
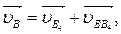
Где 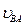- скорость точки В при вращении звена АВ вокруг шарнира А, вектор которой 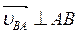; 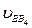- относительная скорость точки В в ее движении относительно точки В₄, вектор которой 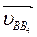||ОС.

Продолжаем построение плана скоростей. Через точку авектора 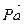проводим прямую, перпендикулярную звену АВпроизвольной длины, а из полюса Рпроводим линию, параллельную оси х-х также произвольной длины. На пересечении получаем искомую точку «в».

После построения плана рассчитываем действительные значения скоростей:

υ_В = µ_υ·[Рв] = 0,18·52 = 9,36 (м/с),

υ_ВА = µ_υ·[ва] = 0,18·30 = 5,4 (м/с).

Скорость точки S₂ определяем по Правилу подобия, п.2. Для этого делим отрезок [aв] пополам, т.к. согласно заданию [as₂]=0,5[ав]. Полученную точку S₂ соединяем с полюсом Р. Находим скорость точки S₂

.

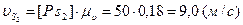Угловые скорости 2-го звена определим по формуле:

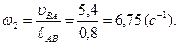
Для определения направления угловой скорости ω₂ необходимо вектор линейных скоростей 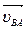перенести (мысленно) в точку «В»на схеме механизма и наблюдать направление поворота точки В относительно точки А. При этом получилось направление w₂ по часовой стрелке.

Построение плана ускорений. Рассмотрим ведущее звено. Полное ускорение точки Аявляется нормальным (а_А = аⁿ_ОА), так как w₁ = const = 30 (рад/с). Поэтому

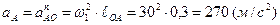
Вычисляем масштаб плана ускорений

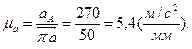
Начинаем построение плана ускорений. Из точки π,принимаемой за полюс (рисунок 2.5, в), проводим отрезок [πа] = 45 мм параллельно звену ОА к центру вращения (к точке О).

При определении ускорений следует помнить, что в группах Ассура II класса 2-го вида всегда известны ускорения внешних пар. В нашем случае

a_В4=0, а_А = 270 (м/с²).

Рассмотрим структурную группу II класса 2 вида (звенья 2-3) . Для определения ускорения а_Вточки В, запишем векторные уравнения

,

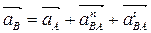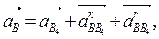
где а_В4 = 0, 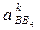- кориолисово ускорение; 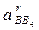- релятивное (относительное) ускорение. Эти два вида ускорения возникают при поступательном движении.

В этих уравнениях известны направления всех векторов:

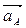|| АО; 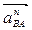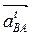|| ВА; ^ВА, 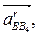|| ОС.

Величины нормального и кориолисово ускорений можно найти по формулам

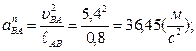
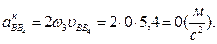
Угловая скорость ω₃=0, т.к. движение звена 3 поступательное.

Тангенциальное и релятивное ускорения найдем построением плана ускорений.

Вычисляем длину вектора 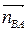, изображающее на плане ускорений ускорение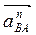

.

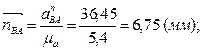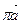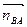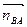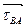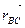Продолжаем построение плана ускорений. Через точку авектора проводим вектор = 6,75 (мм) параллельно звену АВв направлении от точки В к точке А. Из конца вектора проводим прямую, перпендикулярную звену АВпроизвольной длины. Из полюса πпроводим линию, параллельную оси х-х. Точка впересечения двух прямых определит длины векторов и . Модули ускорени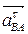й и 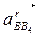, равны:

,

.

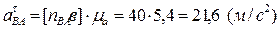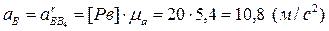Угловое ускорение ε₂ определяем через тангенциальное:

.

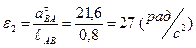Для определения направления ε₂ необходимо вектор тангенциального ускорения 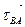приложить (мысленно) в точку В и посмотреть вращение относительно точки А. Направление ε₂ получилось против часовой стрелки.

Ускорение центра масс звена 2 определяем по правилу подобия, п.2. Согласно заданию имеем:

[aS₂] = 0,5 [aв] = 0,5 ∙ 40 = 20 (мм).

Соединив полученную точку S₂ с полюсом π, получим вектор ускорения центра масс. Значение этого ускорения равны:

а_S2 = [πS₂] ∙ µ_а = 30 · 5,4 = 16,2 (м/с²).

Пример 4. Дан кулисный механизм с качающейся кулисой (рисунок 2.6, а). Методом планов определить скорости и ускорения точек А₃, В, а также угловые скорость и ускорений звена 3.

Исходные данные: угловая скорость w₁ = 3 (рад/с), длины звеньев ℓ_O1A = 0,2 (м), ℓ_BO3, = 0,75 (м), ℓ_O1О3 = 0,4 (м). Угол φ=120⁰.

Определить.υ_В, а_В, ω₃, υ_А3, а_А3, ε₃.

Решение. Строение механизма. Число подвижных звеньев n=3, число кинематических пар V класса р₅=4, степень подвижности W=1. Механизм образован присоединением к ведущему звену О₁А и стойке 4 структурной группы II класса 3 вида, состоящей из звеньев 2 и 3. Формула строения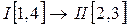

Построение схемы механизма. Рассчитываем масштабный коэффициент длины по формуле (2.1)

,

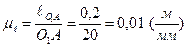где О₁А=20 мм (выбирается произвольно). Тогда

.

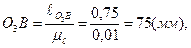
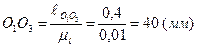Из произвольно выбранной на поле чертежа точки О₁ проводим окружность радиусом R=O₁A=20 мм (траектория движения точки А). Согласно заданию откладываем угол φ=120^о и отмечаем точку А. Далее, от точки O₁ откладываем вниз расстояние O₁O₃= 40 мм. Соединяем точку O₃ с точкой А и продолжаем дальше (длина O₃В = 75 мм). Отмечаем точку В (рисунок 2.6, а).

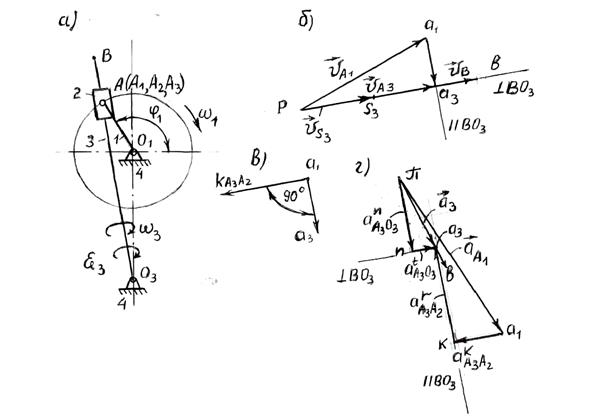
Рисунок 2.6. - Схема кулисного механизма,

его планы скоростей и ускорений

Построение плана скоростей. Рассмотрим ведущее звено. Обозначим точку А₁ на схеме механизма, принадлежащую звену 1, точку А₂, принадлежащую звену 2 и А₃ - звену 3. Скорости точек А₁и А₂известны и по модулю

.

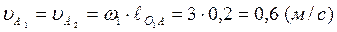Масштаб плана скоростей определим по формуле

.

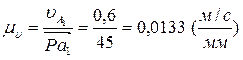Начинаем построение плана скоростей. Из полюса Р(рисунок 2.6, б) проводим вектор 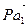длиной 45мм перпендикулярно звену 0₁Ав сторону w₁.

Рассмотрим группу Ассура II класса 3 вида (звенья 2-3). Согласно теореме о плоском движении записываем векторные уравнения:

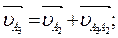
(2.8)

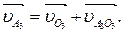
В этом уравнении известны все направления векторов

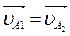^ O₁A, 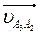|| ВО₃, 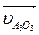^ BO₃.

Продолжаем построение плана скоростей. Из точки а₁проводим прямую, параллельную звену ВО₃, а из полюса Р- прямую, перпендикулярную звену ВО₃. Точка пересечения этих прямых - есть искомая точка а₃.

Положение точки в на плане скоростей находим из условия пропорциональности отрезков (Правило подобия, п.3):

.

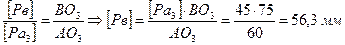Значения длин отрезков подставляем в уравнения в мм, замерив их с плана скоростей и плана механизма.

Действительные значения скоростей вычислим через масштабный коэффициент

υ_В = µ_υ· [Рв] = 0,013 ·56,3 = 0,732 (м/с);

υ_А3А2 = µ_υ· [а₃а₂]= 0,013 ·15 = 0,195(м/с).

Угловую скорость и длину звена рассчитаем по формулам

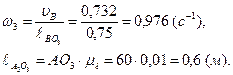(2.9)

Для определения направления ω₃ необходимо вектор скорости 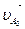приложить (мысленно) в точку А₃ и посмотреть вращение относительно точки О₃. Получилось следующее направление: ω₃ – по часовой стрелке (рисунок 2.6,а).

Построение плана ускорений. Рассмотрим ведущее звено. Полное ускорение точки А₁является нормальным (а_А = аⁿ_АО), так как w₁ = const = 6 (рад/с). Поэтому по формуле (4.8) имеем

.

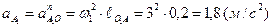Масштабный коэффициент плана ускорений

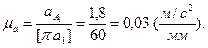
Начинаем построение плана ускорений.Из полюса π (рисунок 2.6, г) проводим вектор 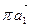= 60 (мм) параллельно звену О₁Аот точки Ак точке O₁.

Рассмотрим группу Ассура II класса 3-го вида (звенья 2-3). Особенность такой группы Ассура заключается в том, что переносным движением является вращательное движение кулисы 3 вокруг точки О₃, а поступательным является движение камня 2 по кулисе 3. Из этого следует, что абсолютное ускорение точки А₃ равно сумме трех ускорений: переносного, относительного и кориолисова. Ускорения внешних пар (шарниров) А₁и О₃ известны по модулю.

a_О3 = 0, а_А1 = 1,8 (м/с²).

Неизвестно ускорение точки А₃ во внутренней поступательной паре. Запишем векторное уравнение для построения плана ускорений

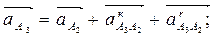
(2.10)

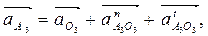
где 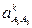- кориолисово ускорение; 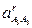- релятивное (относительное) ускорение поступательного движения кулисы 3 относительно камня 2; 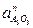- нормальное ускорение точки А₃кулисы 3 в ее вращательном движении вокруг точки О₃; 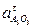- тангенциальное ускорение точки А₃кулисы 3 в ее вращательном движении вокруг точки О₃.

В уравнениях (2.10) направления всех векторов известны

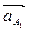|| АО₁; 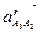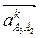|| ВО₃; ^ВО₃; 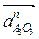|| АО₃; 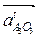^ АO₃; а_Оз = 0.

Для определения направления кориолисова ускорения 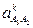необходимо вектор относительной скорости 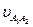повернуть вокруг его начала на 90° в направлении угловой скорости кулисы 3w₃ (рисунок 2.6, в). Получилось, что вектор 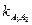будет направлен ^ВО₃ влево.

Найдем величины ускорени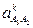й и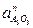

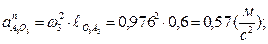
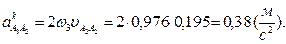
Вычислим масштабные отрезки ускорений

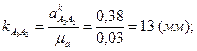
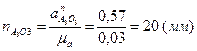. (2.11)

Продолжаем построение плана ускорений. Из конца вектора 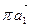проводим вектор 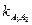=13 (мм). Далее, через конец вектора 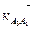проводим прямую, параллельную звену О₃В. Построение 1-го уравнения формулы (2.10) закончили. Начинаем построение 2-го уравнения. Из полюса π плана ускорений проводим вектор 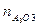параллельно звену ВО₃в направлении от точки А₃ к точке О₃ длиной 20 мм. Через конец вектора 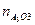проводим прямую, перпендикулярную звену О_зВ. Точка а₃пересечения прямых определит величины отрезков 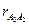и 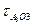. Длину вектора 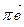на плане ускорений находим из пропорциональности отрезков (Правило подобия, п.3):

.

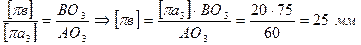Определим действительные значения линейных и угловых ускорений

.

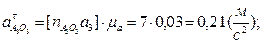
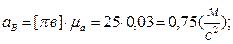
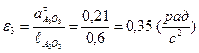Для определения направления ε₃ необходимо вектор тангенциального ускорения 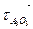приложить (мысленно) в точку А₃ и посмотреть вращение относительно точки О₃. Получилось следующее направление: ε₃ – по часовой стрелке (рисунок 2.6,а).