Первый закон (начало) термодинамики. Внутренняя энергия системы. Энтальпия системы
Первый закон (начало) термодинамики является количественной формулировкой закона сохранения энергии в применении к процессам, связанным с превращениями теплоты и работы. Закон сохранения энергии в самом общем виде был сформулирован М. В. Ломоносовым (1748). Свое дальнейшее развитие данный закон получил в XIX столетии в работах Р. Майера, Г. Гельмгольца, Д. Джоуля.
Закон сохранения энергии утверждает: во вcex явлениях природы энергия не исчезает бесследно и не возникaeт из ничего; она может только превращаться из одной формы в другую в строго эквивалентных соотношениях.
Первый закон имеет несколько равноценных формулировок, но все они выражают и ту же суть: неуничтожимость и эквивалентность энергии при взаимных переходах различных ее видов друг в друга.
Одна из формулировок: вечный двигатель первого рода невозможен, т. е. невозможно создать такую машину, которая производила бы работу без подведения энергии извне.
Другая формулировка: в изолированной системе сумма всех видов энергии есть величина постоянная.
Третья формулировка: в любом процессе приращение внутренней энергии какой-либо системы (∆U = U2 – U1 ) равно количеству сообщенной системе теплоты Q минус количество работы А, совершаемой системой.
Аналитическое выражение имеет вид
∆U = Q – A или Q = ∆U + A. (4.1)
Для процессов, связанных с бесконечно малыми изменениями величин, уравнение принимает вид
ΔQ = dU+δA,
где величины δQ и δА не являются дифференциалами функций состояния, а представляют собой просто бесконечно малые величины, называемые элементарной теплотой и элементарной работой; dU – полный дифференциал внутренней энергии, являющейся функцией состояния. Таким образом, дифференциал внутренней энергии имеет иные математические свойства, чем элементарные теплота δQ и работа δА.
Внутренняя энергия (U) – это энергия, которая в скрытом виде заключена в каждом теле и зависит от его внутреннего состояния. Это та энергия, которая в общем случае представляет собой полный запас энергии тела.
Эту энергию можно представить в виде суммы отдельных составляющих: 1) энергии поступательного движения молекул; 2) энергии вращательных движений молекул; 3) энергии внутримолекулярных колебаний атомов; 4) энергии взаимодействия электронов с ядром; 5) внутриядерной энергии; 6) энергии взаимодействия молекул (потенциальной энергии) и т.д.
Так как при химическом процессе выделяется теплота, то очевидно, U1 > U2. Разность между запасом внутренней энергии в начальном и конечном состояниях ∆U = U1 – U2 преобразуется в форму теплоты Q. Тепловой эффект реакции можно измерить опытным путем, тем самым определится и изменение запаса внутренней энергии системы ∆U, но абсолютный запас внутренней энергии ее до процесса (U1) и после протекания химической реакции (U2) определить невозможно. Если некоторой системе сообщить определенное количество теплоты Q, то в частном случае, когда объем системы не изменяется (V – const), подведенная теплота будет израсходована только на увеличение внутренней энергии: QV = ∆U, или QV = U1 – U2.
Наряду с внутренней энергией в термодинамике часто используют термодинамическую функцию состояния – энтальпию системы.
Энтальпия системы (Н) – это тепловой эффект химической реакции при постоянном давлении (Qр = ∆Н).
Как для любой функции состояния, для энтальпии системы нельзя определить абсолютное значение, а можно определить только изменение в ходе процесса (∆Н = Н1 – Н2). Для стандартных условий (р = 101325 Па, Т = 298 К) ∆U0 и ∆Н0 любого вещества – справочные величины. Для реакции общего вида
аA + вB = сC + dD + ∆Н0реакции
изменение энтальпии реакции при стандартных условиях равно:
∆Н0реакции = (с∆Н0C + d∆Н0D) - (а∆Н0А + в∆Н0B).
Первый закон термодинамики, утверждая неуничтожимость энергии, обосновывает и неуничтожимость материи, поскольку энергия и материя связаны неразрывно друг с другом. Во всех процессах превращения материи неразрывно связаны с превращениями энергии.
Адиабатный процесс – процесс, при котором отсутствует теплообмен между системой и окружающей средой.
Из первого начала термодинамики следует, что работа газа при адиабатном процессе совершается за счет его внутренней энергии:
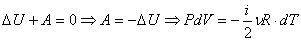 (1).
(1).
С другой стороны, из уравнения Клапейрона-Менделеева следует:
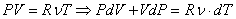 (2).
(2).
Разделим уравнение (2) на уравнение (1):
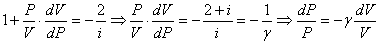 ,
,
Где 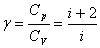 .
.
Проинтегрируем полученное уравнение:
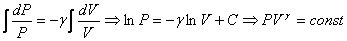 .
.
Таким образом, при адиабатном процессе
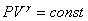 или
или 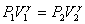 — уравнение Пуассона.
— уравнение Пуассона.
С учетом уравнения Клапейрона-Менделеева ( 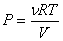 ,
, 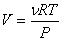 )
)
уравнение Пуассона может быть представлено в виде:
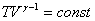 или
или 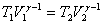
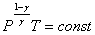 или
или 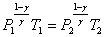 .
.
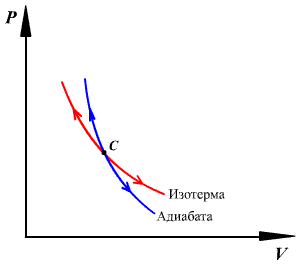
График адиабатного процесса – более крутая кривая, чем гипербола при изотермическом процессе. Это следует из выражения производной 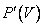 , полученной из уравнения Пуассона.
, полученной из уравнения Пуассона.
Работа газа при адиабатном процессе равна убыли внутренней энергии:
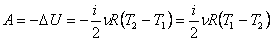 .
.
Термодинамика (формулы)
Внутренняя энергия одного моля одноатомного идеального газа:
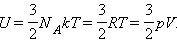
Работа газа при расширении (сжатии):
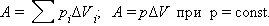
Первый закон термодинамики
ΔU = Q – A; Q = ΔU + A.
Уравнение Пуассона для адиабаты:
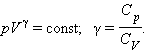
Работа газа в адиабатическом процессе:
A = CV(T2 – T1).
Формула Р.Майера:
Cp = CV + R.
Молярная теплоемкость при постоянном объеме: 1

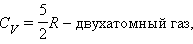

Молярная теплоемкость твердого тела:
C = 3R
КПД теплового двигателя:
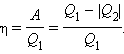
КПД идеальной тепловой машины, работающей по циклу Карно:
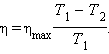
Энтропия:
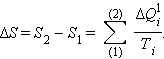
Закон возрастания энтропии:
ΔS >= 0.
Формула Больцмана:
S = k ln W.
Тепловое расширение тел:
l = l0 (1 + αΔT);
<m>V = V0 (1 + βΔT); β ≈ 3α.m>
Дата добавления: 2015-06-01; просмотров: 1467;
