Тензор деформацій та напруг. Закон Гука.

Тензор деформації - тензор , який характеризує стиснення (розтягнення) і зміна форми в кожній точці тіла при деформації .

Тензор деформації Коші-Гріна в класичній суцільному середовищі (частки якої є матеріальними точками і володіють лише трьома трансляційними ступенями свободи) визначається як

,

де 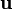- Вектор, що описує зсув точки тіла: його координати - різниця між координатами близьких точок після ( 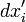) І до ( 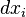) Деформації. Диференціювання проводиться за координатами в відлікової конфігурації (до деформування). Відстані до і після деформації пов'язані через :

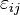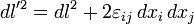
(По повторюваним індексам ведеться підсумовування).

За визначенням тензор деформації симетричний, тобто .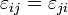

У деяких джерелах цей тензор деформації називають тензором деформації Гріна-Лагранжа, а праву міру деформації Коші-Гріна (подвоєний обговорюваний тензор деформації плюс одиничний тензор) - правим тензором деформації Коші-Гріна.

Нелінійний тензор деформації Коші-Гріна має властивість матеріальної об'єктивності. Це означає, що якщо шматок тіла, що деформується здійснює жорстке рух, тензор деформації повертається разом з елементарним об'ємом матеріалу. Зручно використовувати такі тензори при записі визначальних рівнянь матеріалу, тоді принцип матеріальної об'єктивності виконується автоматично, тобто якщо спостерігач рухається щодо деформируемой середовища, поведінка матеріалу не змінюється (тензор напружень повертається в системі відліку спостерігача разом з елементарним об'ємом матеріалу).

Існують також інші об'єктивні тензори деформації, наприклад, тензор деформації Альманси, тензори деформації Піола, Фингера і т. д. У деякі з них входять похідні від переміщень по координатах в відлікової конфігурації (до деформування), а в деякі - за координатами в актуальній конфігурації (після деформування).

Те, що в класичній суцільному середовищі енергія деформації залежить лише від симетричного тензора деформації, випливає з закону балансу моментів. Будь взаємно-однозначна функція об'єктивного тензора деформації буде також об'єктивним тензором деформації. Наприклад (в силу симетричності і позитивної визначеності тензора деформації) можна використовувати квадратний корінь з тензора деформації Коші-Гріна. Однак, задаючи визначальні рівняння за допомогою цих тензорів, важливо стежити за припущеннями про характер залежності вільної енергії (або напруг) від тензорів деформації. Ясно, що припущення про, скажімо, дифференцируемости вільної енергії по тензору деформації Коші-Гріна, по кореню з нього або за його квадрату приведуть до рівнянь абсолютно різних матеріалів. Лінійна по 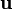теорія загального вигляду при малих 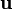вийде лише в першому випадку.

При малих 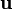можна знехтувати квадратичними доданками, і користуватися тензором деформації у вигляді:

Лінійний тензор деформації Коші-Гріна (збігається з лінійним тензором деформації Альманси з точністю до знака) не має властивість матеріальної об'єктивності при великих поворотах, тому його не використовують у визначальних рівняннях для великих деформацій. У наближенні малих поворотів це властивість зберігається.

Діагональні елементи 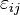описують лінійні деформації розтягування або стиснення, недіагональні - деформацію зрушення.

У сферичній системі координат

.

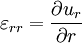
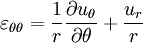
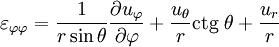
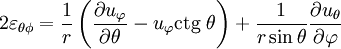
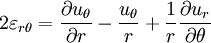
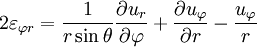У циліндричній системі координат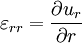

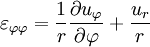
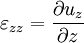
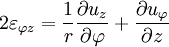
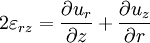
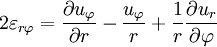
Закон Гука встановлює лінійну залежність між деформацією й механічними напруженнями.

Закон Гука справедливий для малих пружних деформацій.

Закон Гука для випадку одновісного напруженого стану

У своїй найпростішій формі закон Гука записується для деформації довгого тонкого стрижня або пружини

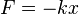, де F — сила, k — коефіцієнт жорсткості, х — видовження.

Ця формула не враховує зміни поперечних розмірів стрижня при розтягу. Крім того коефіцієнт жорсткості — це властивість стрижня, а не властивість матеріалу, з якого він виготовлений.

Запис закону Гука через напруження і відносні деформації дає можливість виключити вплив конструктивних особливостей стрижня на вид залежності між силовим параметром і деформацією. Для випадку лінійного навантаження закон Гука має вигляд:

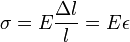, де: σ — механічне напруження, визначається, як сила, що припадає на одиницю площі поперечного перерізу тіла;

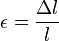— величина відносної деформації (відносне видовження);

E — модуль Юнга.

Закон Гука для тривимірного напруженого стану

Закон Гука для тривимірного (складного) напруженого стану у випадку ізотропного матеріалу може бути записаний у вигляді системи рівнянь:

для лінійних деформацій

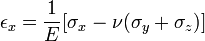
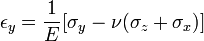
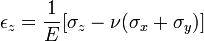
для деформацій зсуву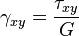

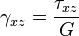
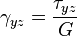
де:

ε — деформація розтягу-стиску в точці,

σ — напруження розтягу-стиску,

γ — деформація зсуву (кутова) в точці,

τ — напруження зсуву (дотичне напруження) в точці,

G — модуль зсуву,

E — модуль Юнга

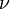— коефіцієнт Пуассона.

Закон можна сформулювати так: компоненти тензора деформації в даній точці тіла знаходяться в лінійній залежності від компонентів тензора напруження тієї ж точки.

Строга форма запису закону Гука

,

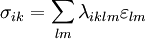де 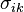— тензор механічних напружень, 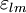— тензор деформації, а 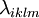— тензор чертвертого рангу, який називається тензором модулів пружності і є характеристикою речовини.

Закон Гука був сформульований Робертом Гуком у 1660.