Мікроканонічний розподіл. Функція розподілу ізольованої термодинамічної системи.
Гіббса розподіл мікроканонічний
Розподіл Ґіббса — розподіл, що визначає кількості частинок в різних квантових станах. Ґрунтується на таких постулатах статистики:
Всі доступні мікростани системи рівноймовірні.
Рівновазі відповідає найімовірніший розподіл (підсистем за станами).
Ймовірність перебування підсистеми в деякому стані визначається лише енергією стану.
Розподіл Ґіббса являє собою найзагальнішу і зручну основу для побудови рівноважної статистичної механіки.
Статистична сума
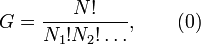 як і в термодинаміці, має зміст відносної ймовірність знаходження системи в певному микростанів. І, дивлячись на співвідношення Больцмана
як і в термодинаміці, має зміст відносної ймовірність знаходження системи в певному микростанів. І, дивлячись на співвідношення Больцмана 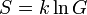 , легко зрозуміти, що станом з мінімальною ентропією відповідає мінімальна статистична вага. Потрібно врахувати, що в системі постійні число частинок
, легко зрозуміти, що станом з мінімальною ентропією відповідає мінімальна статистична вага. Потрібно врахувати, що в системі постійні число частинок
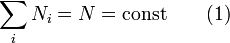 і повна енергія
і повна енергія 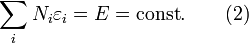
Факторіал великих чисел (а числа 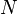 і
і 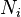 великі; тими з них, які малі, можна знехтувати) находится за формулою Стірлінга:
великі; тими з них, які малі, можна знехтувати) находится за формулою Стірлінга: 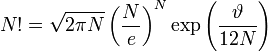 , де
, де 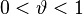 . Цю точну формулу можна замінити наближеною
. Цю точну формулу можна замінити наближеною
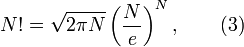
так як відносна помилка в обчисленнях за цією формулою не перевершує 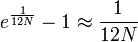 , вже при
, вже при  вона менше одного відсотока. Із співвідношень (0), (1) і (3) випливає наступне:
вона менше одного відсотока. Із співвідношень (0), (1) і (3) випливає наступне:
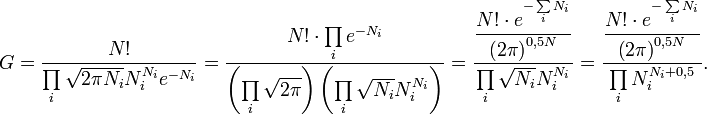
Чисельник тут є функція від 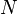 , і можна ввести позначення
, і можна ввести позначення
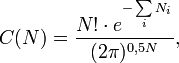 що дає
що дає 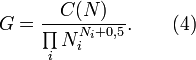
Тоді з формули Больцмана 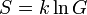 слідує
слідує
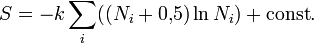
Тут можна знехтувати 0,5 порівняно з 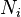 . Тоді
. Тоді
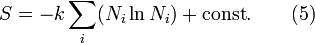
Максимум ентропії (5) із урахуванням співвідношеньий (1) і (2), використовуючи метод невизначених множників, буде при умовах
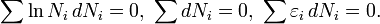
Отсюда 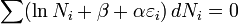 , де
, де 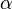 и
и  — множники Лагранжа, не залежні від змінних
— множники Лагранжа, не залежні від змінних 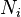 . У системі є
. У системі є 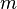 змінні і три рівняння - отже, будь-які дві залежать від інших; відповідно можна вважати залежними
змінні і три рівняння - отже, будь-які дві залежать від інших; відповідно можна вважати залежними 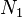 та
та 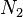 і вибрати множники Лагранжа так, щоб коефіцієнти при
і вибрати множники Лагранжа так, щоб коефіцієнти при 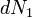 и
и 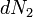 звернулися в 0. Тоді при інших
звернулися в 0. Тоді при інших  змінні
змінні 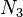 ,
, 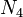 , … можна прийняти за незалежні, і при них коефіцієнти також будуть рівні 0. Так отримано
, … можна прийняти за незалежні, і при них коефіцієнти також будуть рівні 0. Так отримано
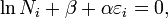 звідси
звідси 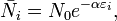 де
де 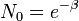 — нова константа.
— нова константа.
Для визначення сталої 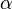 можна скласти систему в теплопровідні стінки і квазістатично змінювати її температуру. Зміна енергії газ а одно
можна скласти систему в теплопровідні стінки і квазістатично змінювати її температуру. Зміна енергії газ а одно 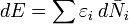 , а змінаентропії (зі співвідношення (5)) дорівнює
, а змінаентропії (зі співвідношення (5)) дорівнює 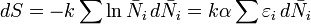 . Так як
. Так як 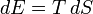 , то звідси
, то звідси 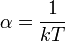 , і тому
, і тому
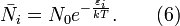
Термостат
Отримано найбільш ймовірне розподіл системи. Для довільної макроскопічної системи (системи в термостаті), оточеній протяжної середовищем (термостатом), температура якої підтримується постійною, виконується співвідношення (6) - розподіл Гіббса: їм визначається відносна ймовірність того, що система при термодинамічній рівновазі знаходиться в 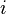 -ом квантовом состоянии.
-ом квантовом состоянии.
Дата добавления: 2015-06-01; просмотров: 1613;
