Конденсаторы.

Для того чтобы проводник обладал емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел
потенциалах накапливать значительные по величине заряды, иными словами,
обладать большой емкостью. Эти устройства получили название конденсаторов.

Если к заряженному проводнику приближать другие тела, то на них возни­кают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду Q будут заряды противоположного знака. Они, естественно, ослабляют поле, создаваемое зарядом Q, т.е. понижа­ют потенциал проводника, что приводит к повышению его электроемкости.

Конденсатор состоит из двух проводников (обкладок), разделенных ди­электриком. На его емкость не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накап­ливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: две плоские пластины, два коак­сиальных цилиндра, две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные за­ряды, возникающие на разных обкладках, являются равными по модулю разно­именными зарядами. Под емкостью конденсатора понимается фи­зическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов ( 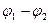) между его обкладками.

(1.16.1)

Рассчитаем емкость плоского конденсатора, состоящего из двух парал­лельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и -Q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эф­фектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать, используя формулы ( ) и (1.16.1). При наличии диэлектрика между обкладками разность потенциалов между ними:

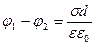(1.16.2)

где - диэлектрическая проницаемость. Тогда из формулы (1.16.1), заменяя , с учетом (1.16.2) получим выражение для емкости плоского конденсатора:

(1.16.3)

Емкость конденсатора любой формы прямо пропорциональна диэлектри­ческой проницаемости диэлектрика, заполняющего пространство между об­кладками. Поэтому применение в качестве прослойки сегнетоэлектриков зна­чительно увеличивает емкость конденсаторов.

Конденсаторы характеризуются пробивным напряжением - разностью потенциалов между обкладками конденсатора, при которой проис­ходит пробой - электрический разряд через слой диэлектрика в конденсато­ре. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины

Для увеличения емкости и варьирования ее возможных значений конден­саторы соединяют в батареи, при этом используется их параллельное и после­довательное соединение.

1. Параллельное соединение конденсаторов (рис.1.16.2).

У параллельно соединенных конденсаторов разность потенциалов на обкладках
одинакова и равна . Если емкость отдельных конденсаторов С₁, С₂, ..., С_п. то,
согласно (1.16.1), их заряды равны

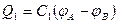
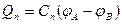
Рис.1.16.2

а заряд батареи конденсаторов

Полная емкость конденсатора

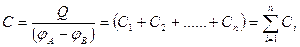
т.е. при параллельном соединении конденсаторов она равна сумме емкостей от­
дельных конденсаторов.

2. Последовательное соединение конденсаторов (рис 1.16.3). У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи 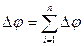, где для любого из рассматриваемых конденсаторов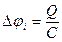

С другой стороны,

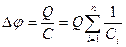
откуда

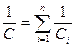
Рис.1.16.3

т.е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при последовательном соединении конден­саторов результирующая емкость С всегда меньше наименьшей емкости, ис­пользуемой в батарее