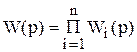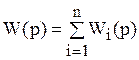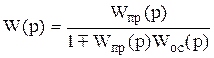Типовые соединения звеньев

Рис. 9.1

Запишем систему уравнений, описывающих такое соединение:

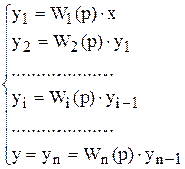. (9.1)

Исключив все промежуточные переменные, получаем:

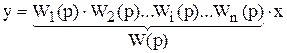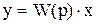; . (9.2)

Из полученного выражения видно, что передаточная функция системы, состоящей из последовательно соединенных звеньев, равна произведению передаточных функций этих звеньев:

(9.3)

Рис. 9.2

Запишем систему уравнений, описывающих такое соединение:

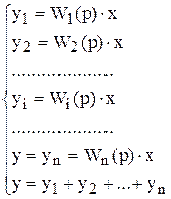. (9.4)

Исключив все промежуточные переменные, получаем:

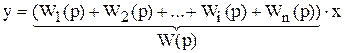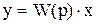; . (9.5)

Можно сформулировать следующее правило: передаточная функция параллельного соединения звеньев, равна сумме передаточных функций этих звеньев:

(9.6)

Пример: В качестве примера рассмотрим моделирование астатического изодромного звена, передаточная функция которого: W(s) = 1 + .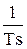

Другими словами, это параллельно включенные два звена: статическое безинерционное и астатическое 1-го порядка (идеальное). С другой стороны, эту передаточную функцию можно записать подругому:

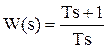
и промоделировать одним блоком.

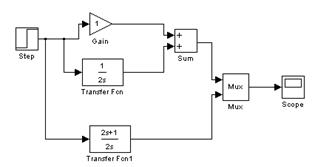
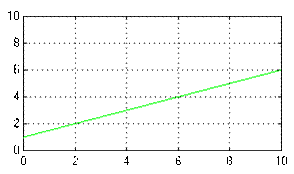
Рис. 9.3 – Схема и результат моделирования изодромного звена двумя способами: с помощью параллельного соединения звеньев и одной передаточной функцией

3. Соединения с обратной связью

 

 

Рис. 9.4

 

где W_пp(p), W_oc(p) - передаточные функции прямой и обратной связи;

y_c, y_oc - промежуточные переменные.

Система уравнений, описывающих такое соединение:

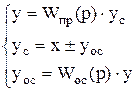. (9.7)

Определим из нее y:

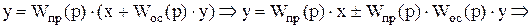(9.8)

Þ .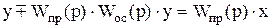

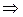
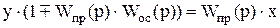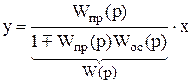Þ (9.9)

(9.10)

 

 

Итак, получаем правило: передаточная функция системы с обратной связью равна дроби, числитель которой равен передаточной функции прямой цепи W_пр(p), а знаменатель равен l произведение передаточных функций, входящих в замкнутый контур. Знак суммирования в знаменателе противоположен знаку обратной связи.