Частотная передаточная функция и частотные характеристики

Если на вход линейного звена или системы звеньев подать гармонический сигнал, то на выходе после окончания переходного процесса также будет гармонический сигнал. Причем частота выходного сигнала, всегда будет равна частоте входного.

(Вспомните результаты лабораторной работы, когда гармонический (синусоидальный) сигнал подавали на вход безинерционного звена (масштабирующий блок Gain)).

Рассмотрим пример. Подадим на вход блока, моделирующего статическое колебательное инерционное звено синусоидальный сигнал 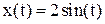и посмотрим какой сигнал y(t) получится на выходе данного звена.

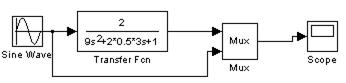
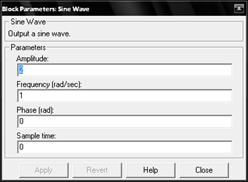
Рис. 10.1 – Схема моделирования	Рис. 10.2 – Настройки блока, моделирующего синусоидальный сигнал
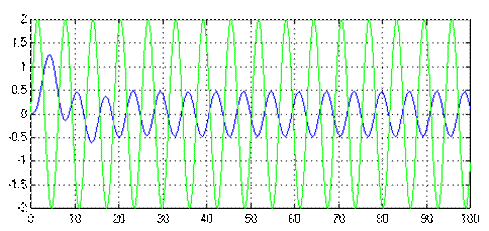Рис. 10.3 – Сигналы на входе x(t) и выходе y(t) колебательного звена

Как видно по рис. 10.3, после прохождения через колебательное звено и окончания переходного процесса мы наблюдаем гармонический процесс с частотой равной частоте входного сигнала. Амплитуда и сдвиг фаз выходного процесса изменились по сравнению с входным.

Частотными характеристиками звена (системы) называются характеристики изменения параметров динамически установившихся гармонических колебаний на выходе системы в функции значения частоты (w) гармонического сигнала входного воздействия, когда w Î (-¥; ¥). Для графического отображения характеристик, как правило, используют положительную полуось частоты. Существую следующие виды частотных характеристик:

- амплитудочастотная характеристика (АЧХ);

- фазочастотная характеристика (ФЧХ);

- амплитудофазочастотная характеристика (АФЧХ).

АЧХ (А(w)) звена (системы) - отношение амплитуды выходного гармонического сигнала к амплитуде входного в функции его частоты w в установившемся режиме. Т.е. если x(t) = x^maxsinwt – входной сигнал;

y(t) = y^maxsin(wt + φ) – выходной сигнал, то

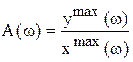, w Î (-¥, ¥). (10.1)

ФЧХ (j(w)) звена (системы) называется разность фаз между выходным и входным сигналами в установившемся режиме.

j(w) = j_y(w) – j_x; (10.2)

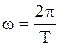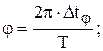j_x = const ≡ 0; ; w Î (-¥, ¥).

Рис. 10.4 – Графики входного и выходного сигналов с построениями необходимыми для определения параметров, для расчета АЧХ и ФЧХ

АФЧХ – это годограф радиус-вектора, длина которого – АЧХ, а угол поворота – ФЧХ.

Частотная передаточная функция – отношение изображений Фурье выходного и входного сигналов.

,

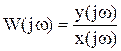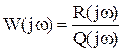
где 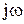- оператор Фурье.

Для линейных устойчивых систем при нулевых начальных условиях возможен взаимный однозначный переход между передаточными функциями систем в непрерывном времени. Для таких процессов преобразование Лапласа переходит в преобразование Фурье, если произвести подстановку s = jw.

Частотная ПФ связана с частотными характеристиками следующим образом: частотная передаточная функция 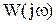представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной (АЧХ), а аргумент – сдвигу фаз выходной величины по отношению к входной(ФЧХ).

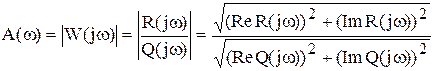; (10.4)

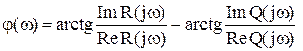
Частотную передаточную функцию можно представить в алгебраической форме:

W(jω) = U(ω) + jV(ω) = ReW(jω) + jImW(jω).

Взаимосвязь между различными формами представления W(jω):

;

.

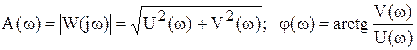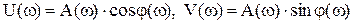U(ω) и V(ω) можно получить непосредственно из W(jω). Для этого необходимо представить частотную ПФ в следующем виде:

.

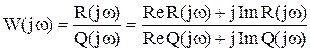Затем умножить числитель и знаменатель на выражение комплексно сопряженное знаменателю. Затем выделить действительную и мнимую части.

Пример: получение частотной передаточной функции из передаточной функции в форме изображений по Лапласу для статического апериодического инерционного звена 1-го порядка.

W(s) =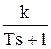

Общая форма частотной ПФ получается формальной заменой оператора s на 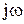: W(jw) = .

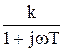Чтоб перейти к алгебраической форме помножим числитель и знаменатель на выражение комплексно-сопряженное знаменателю

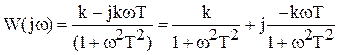
Вывести частотные ПФ самостоятельно для всех звеньев.

Итак, частотные характеристики можно построить различными способами:

1. Можно аналитически получить частотную передаточную функцию звена (системы), а затем промоделировать выражения (10.4).

2. Можно подавать на вход звена (системы) гармонические входные воздействия с различной частотой и вычислять АЧХ и ФЧХ по формулам (10.1), (10.2).

Эти два метода являются достаточно трудоемкими, особенно когда речь идет о построении частотных характеристик сложных систем.

3. Можно воспользоваться средствами компьютерного моделирования. Специальный блок, разработанный в Simulink – «Анализатор частотных характеристик» производит построение АЧХ, ФЧХ и АФЧХ звена или системы. Рассмотрим, как работает блок и как проводить компьютерные эксперименты по снятию частотных характеристик звена (системы).