Вырезания узлов
Вырезаем узел, где приложена активная сила F3, и изображаем его на чертеже. Реакции S11, S12 растянутых стержней 11, 12 направлены от узла (рис. 1.53).
Система сил (F3, S11, S12), действующая на узел, плоская сходящаяся. Аналитические условия равновесия такой системы сил выражаются системой уравнений:
Σ 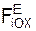 + Σ
+ Σ 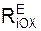 = 0 = – S12 – S11·cos(α) = 0; (1)
= 0 = – S12 – S11·cos(α) = 0; (1)
Σ 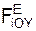 + Σ
+ Σ 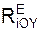 = 0 = – F3 + S11·sin(α) = 0. (2)
= 0 = – F3 + S11·sin(α) = 0. (2)
 |
Решая эту систему уравнений, получим:
из уравнения (2)
S11 = F3/sin(α) = 2/0,5 = 4,000 кН;
из уравнения (1)
S12 = – S11·cos(α) = – 4·0,866 = – 3,464 кН.
Так как значение S11 > 0, а значение S12 < 0, то стержень 11 растянут, а стержень 12 сжат.
Аналитический расчёт сразу же следует проверить графическим построением замкнутого силового многоугольника. Система сил (F3, S11,S12) уравновешенная, поэтому силовой треугольник, построенный на силах F3,S11,S12,должен быть замкнут. Силовой треугольник строится в выбранном масштабе (см. рис. 1.53). Построение начинается с известной силы F3.На силовом многоугольнике определяется истинное направление реакций растянутых стержней.
Графическая проверка подтвердила, что стержень 11 растянут, а стержень 12 сжат.
Графическую проверку рекомендуется выполнять сразу же после аналитических расчётов, так как этим устраняются ошибки в последующих расчётах.
 |
Так как теперь известны реакции S11,S12растянутых стержней, то вырезается следующий узел, к которому приложена активная сила F2 (рис. 1.54).
Вырезанный узел находится в равновесии под действием сходящейся системы сил (F2, S12, S10, S9). Необходимо ещё раз отметить, что реакции растянутых стержней направляются от узла. Аналитические условия равновесия вырезанного узла выражаются системой уравнений:
Σ 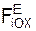 + Σ
+ Σ 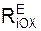 = 0 = – S9 + S12 = 0; (1)
= 0 = – S9 + S12 = 0; (1)
Σ 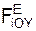 + Σ
+ Σ 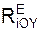 = 0 = – F2 + S10 = 0. (2)
= 0 = – F2 + S10 = 0. (2)
Из уравнения (1) S9 = S12 = – 3, 464 кН < 0;
из уравнения (2) S10 = F2 = 9,000 кН > 0.
Таким образом, стержень 9 сжат, а стержень 10 растянут. Этот расчёт проверяется графическим построением силового многоугольника (см. рис. 1.54).
Необходимо отметить, что построение силового многоугольника начинают с известных сил F2 и S12, а точка пересечения линий действия реакций S9, S10 определит их направление и модуль. При этом если известно, что стержень сжат (стержень 12), то его реакцию (S12) направляют к узлу.
Графическое построение подтвердило правильность проведенных расчётов.
Определение остальных реакций Si растянутых стержней проводится аналогичным способом. Результаты вычислений сводятся в таблицу.
Таблица
| Реакции внешних связей | Реакции растянутых стержней | ||||||||
| RA, кН | XB, кН | YB, кН | S1, кН | Si, кН | S10, кН | S11, кН | S12, кН | ||
| 11,198 | 15,198 | 11,000 | 9,000 | 4,000 | –3,464 |
Усилия в отдельных стержнях загруженной фермы могут оказаться нулевыми. Такие стержни принято называть нулевыми.
Рассмотрим леммы, пользуясь которыми можно определить нулевые стержни плоской фермы, не производя её расчета.
 |
Лемма 1. Если в незагруженном узле плоской фермы сходятся два стержня, то усилия в этих стержнях равны нулю (рис. 1.55).
Лемма 2. Если в незагруженном узле плоской фермы сходятся три стержня, из которых два расположены на одной прямой, то усилие в третьем стержне равно нулю. Усилия в первых стержнях равны между собой (рис. 1.56).
 |
Лемма 3. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне равно по модулю приложенной внешней силе, а усилие в другом стержне равно нулю (рис. 1.57).
 |
1.21.3. Определение усилий в стержнях фермы
способом Риттера
Этим способом удобно пользоваться для определения усилий в стержнях при проверочных расчётах.
Идея способа Риттера заключается в следующем.
1. Ферму разрезают на две части сечением, проходящим только через три стержня.
2. Рассматривают равновесие одной из частей фермы, которая находится в равновесии под действием активных сил, реакций внешних связей и реакций растянутых стержней. При этом реакции растянутых стержней прикладываются к стержням в местах их разреза.
3. Определяют точки Риттера (I, II, III). Точки Риттера – точки, где пересекаются линии действия реакций растянутых стержней.
4. Составляют уравнения равновесия рассматриваемой части фермы в одной из двух форм.
Форма 1:
Σ M(I)(FiE) + Σ M(I)(RiE) = 0;
Σ M(II)(FiE) + Σ M(II)(RiE) = 0;
Σ M(III)(FiE) + Σ M(III)(RiE) = 0.
Форма 2:
Σ M(I)(FiE) + Σ M(I)(RiE) = 0;
Σ M(II)(FiE) + Σ M(II)(RiE) = 0;
Σ 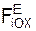 + Σ
+ Σ 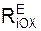 = 0.
= 0.
5. Из этих уравнений равновесия находят неизвестные реакции растянутых стержней.

На рис. 1.58 изображена ферма и одна из её отрезанных частей.
Поскольку разрезанные стержни не параллельны, то имеется три точки Риттера (точки I, II, III). В этом случае для определения реакций растянутых стержней используется первая форма уравнений равновесия.
Σ M(I)(FiE) + Σ M(I)(RiE) = 0 =
= – F2·b– F3·2·b + S7·2·b·sin(α) = 0; (1)
S7 = 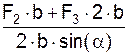 =
= 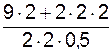 = 13,000 кН.
= 13,000 кН.
Σ M(II)(FiE) + Σ M(II)(RiE) = 0 = – F3·b – S9·b·tg(α) = 0; (2)
S9 = – 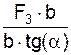 = –
= – 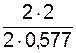 = – 3,464 кН.
= – 3,464 кН.
Σ M(III)(FiE) + Σ M(III)(RiE) = 0 = – F3·b + S8·2·b·sin(α) = 0; (3)
S9 = 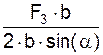 =
= 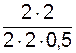 = 2,000 кН.
= 2,000 кН.
Если в сечении фермы стержни параллельны, то используется вторая форма уравнений равновесия, так как имеется только две точки Риттера (рис. 1.59).

Согласно определению (точки Риттера), точка (I) Риттера находится в месте пересечения линий действия векторов S5, S6, а точка (II) Риттера расположена в месте пересечения линий действия векторов S6, S7.
Дано: F1 = 2 кН; F2 = 5 кН; F3 = 10 кН; b = 2 м; α = 45о.
Дата добавления: 2015-05-30; просмотров: 1335;
