Математическое ожидание функции от случайной величины. Свойства математического ожидания

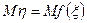Пусть — функция от случайной величины. Определим математическое ожидание . Это возможно сделать двумя способами. Первый способ состоит в том, что сначала строится распределение случайной величины , затем уже находим . Мы рассмотрим другой способ. Пусть сначала — дискретная случайная величина, принимающая значения 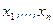. Тогда случайная величина принимает значения 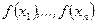с теми же вероятностями 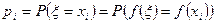. В этом случае математическое ожидание определяется по формуле

. (6.2.1)

В случае, если случайная величина принимает счетное число значений, то математическое ожидание случайной величины определяется по формуле

. (6.2.2)

При этом условие существования математического ожидания (6.1.4) примет вид:

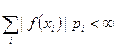. (6.2.3)

Пример 6.Случайная величина имеет ряд распределения:

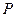
	0,7	0,1	0,2

Найти математическое ожидание математической величины: .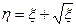

m Решение. Для решения задачи применим формулу (6.2.1).

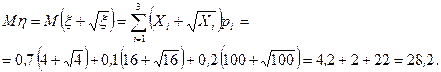
Таким образом, математическое ожидание математической величины 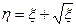равно 28,2. l

Пусть — непрерывная случайная величина, имеющая плотность распределения 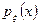. Пусть функция непрерывная (за исключением, быть может, счетного числа точек). Тогда математическое ожидание случайной величины определяется по формуле

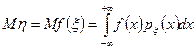. (6.2.4)

Условие существования математического ожидания случайной величины имеет вид:

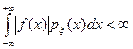. (6.2.5)

Пример 7.Случайная величина имеет нормальное распределение с параметрами , т.е. ее плотность имеет вид:

.

Найти математическое ожидание случайной величины .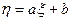

m Решение. Используя формулу (6.2.4), получаем:

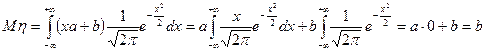. l

Пример 8.Случайная величина распределена равномерно в интервале 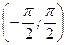, т.е.

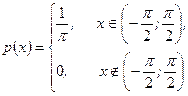
Найти математическое ожидание случайной величины .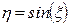

m Решение. Используя формулу (6.2.4.) , получаем:

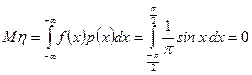. l