Непрерывные случайные величины

Как уже говорилось, непрерывной называется случайная величина, возможные значения которой непрерывно заполняют какую-то область. Дадим более строгое определение непрерывной случайной величины.

Определение. Случайная величина 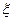называется непрерывной, если ее функцию распределения 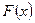можно представить в виде:

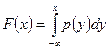. (5.4.1)

Определение. Функция 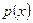, присутствующая в (5.4.1), называется плотностью распределения (вероятностей) случайной величины .

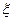Отметим, что все реально встречающиеся плотности распределения являются непрерывными (за исключением, быть может, конечного числа точек) функциями, и, следовательно, для них плотность распределения 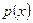представляет собой производную функции распределения 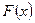, т. е.

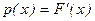. (5.4.2)

Свойства плотности распределения:

1. Плотность является неотрицательной функцией, т.е.

.

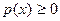Доказательство. Функция распределения — неубывающая функция. Следовательно, ее производная, которая по (5.4.2.) является плотностью, есть неотрицательная функция. n

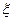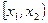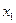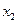2. Вероятность попадания случайной величины в интервал равна определенному интегралу от ее плотности в пределах от до , т.е.

.

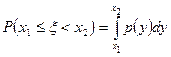Доказательство. С одной стороны, по свойству 5 функции распределения

,

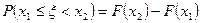c другой стороны, в силу (5.4.2):

.

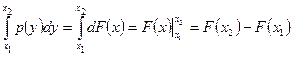3. Условие нормировки: несобственный интеграл от плотности случайной величины в бесконечных пределах равен единице, т.е.

.

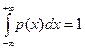Доказательство. В силу свойства 2, имеем

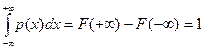. n

4. .

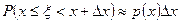Доказательство. Из свойства 2 следует, что вероятность попадания случайной величины на интервал 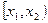численно равна площади криволинейной трапеции (рис. 5.1).

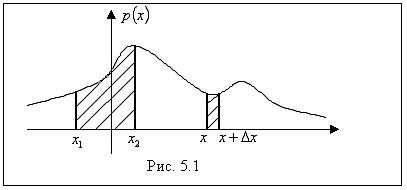
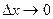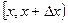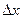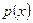Как видно из рис. 5.1, при вероятность попадания на интервал приближенно совпадает с площадью прямоугольника со сторонами и . n

5. Для непрерывных случайных величин .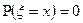

Доказательство. Достаточно применить свойство 4, где 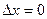. n

6. Для непрерывных случайных величин свойство 2 можно переписать в виде:

.

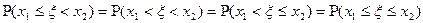Пример 7. Случайная величина 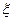имеет плотность

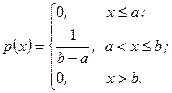
График функции 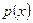изображен на рис. 5.2.

Найти функцию распределения 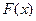случайной величины 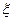и изобразить ее график.

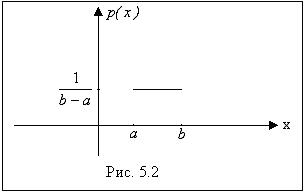
m Решение. Для решения задачи применим формулу (5.4.1).

При 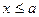получаем, что

.

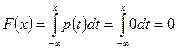При 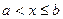получаем:

.

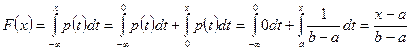При 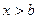имеем:

.

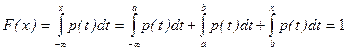Таким образом, получаем

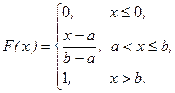
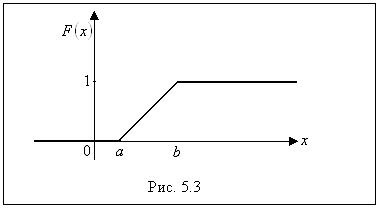
График функции распределения изображен на рис. 5.3. l

Пример 8. Случайная величина 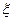подчинена закону Симпсона («закону равнобедренного треугольника») на участке 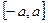(рис. 5.4).

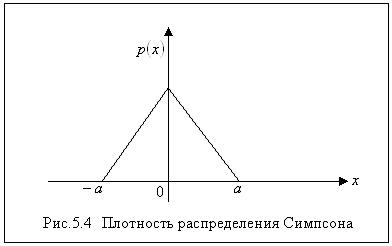
Найти плотность распределения и функцию распределения.

m Решение. Используя свойство 3 плотности, найдем высоту треугольника:

.

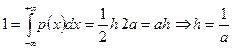Далее находим уравнения ребер:

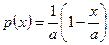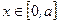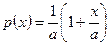, при ;

, при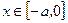

или

.

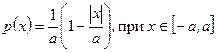Найдем функцию распределения .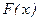

Очевидно, что при 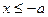функция распределения равна нулю, т.е. .

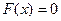Далее, при :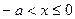

.

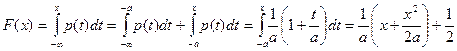При :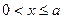

.

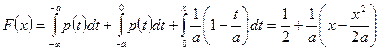При 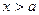, получаем .

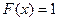Таким образом, получено

,

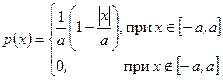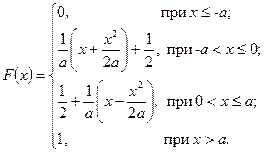
l