КОЛЕБАНИЯ НЕУРАВНОВЕШЕННЫХ РОТОРОВ

Нелинейные свойства подшипников качения вносят особенности в характер вынужденных колебаний неуравновешенных роторов (в практике не существует идеально уравновешенных роторов). Контактная податливость в случае жестких роторов существенно понижает критические скорости, причем резонансные пики могут раздваиваться.

Для стандартных подшипников со сферическими телами качения между деформацией и радиальной нагрузкой существует зависимость

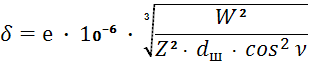, (1)

где δ – сближение центров внутреннего и наружного колец подшипника в направлении действия нагрузок вследствие упругих контактных деформаций, см;

е – коэффициент, зависящий от типа подшипника (е = 280 – для радиального и радиально-упорного; е = 264 – для радиального сферического; е = 55 – для радиального сферического с бочкообразными роликами);

W – радиальная нагрузка на подшипник, кг;

Z – число тел качения;

d_ш – диаметр тел качения, см;

ν – угол контакта тел качения, град.

Из зависимости (1) можно определить W – радиальную нагрузку на подшипник, кг

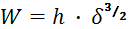, (2)

где h = 10⁹ ∙ e^-3/2 ∙ z ∙ d_ш^1/2 ∙ сos ν.

В основном используют зависимость (2), хотя она характеризует только усредненную связь между нагрузкой и деформацией и не учитывает незначительных изменений жесткости из-за перекатывания тел качения.

Приближенный способ учета влияния податливости подшипников качения на критические скорости (собственные частоты) заключается в том, что при дифференцировании зависимости (2) по δ находят «жесткость» подшипника при статической нагрузке W = W_o

С_ш = dW / dδ ‌|_W=Wo = 3/2 ∙ h^2/3 ∙ W^1/3 ‌. (3)

Для радиальных и радиально-упорных подшипников формула (3) имеет следующий вид

С_ш = 5350 ∙ ³√d_м ∙ W_o ∙ Z² ∙ cos² γ . (4)

Значение С_ш, кг/см используют при расчете собственных частот колебаний, совпадающих с направлением действия статической нагрузки. Эксперименты показывают, что использование формулы (4) приводит к несколько заниженным результатам для собственных частот, особенно для легко нагруженных роторов. Это объясняется тем, что кроме статической нагрузки (весовой) на подшипники в собранной машине действуют нагрузки, вызванные неизбежными перекосами.

Величина среднего радиального зазора между наружным и внутренним кольцами подшипника и телами качения равна ∆. Силы контактной упругости в подшипнике определяются зависимостью (1), где упругое перемещение δ определяется следующим образом (см. рис. 1)

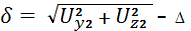. (5)

Предполагается, что силы демпфирования в подшипниках качения содержат как линейную, так и нелинейную составляющие (рис. 1). Тогда проекции сил, возникающие в подшипниках, запишутся в определенном виде (формулы не приводятся, см. [2, С. 38–39]). Значения Р_у и Р определяются из соответствующих выражения [2, С. 38–39].

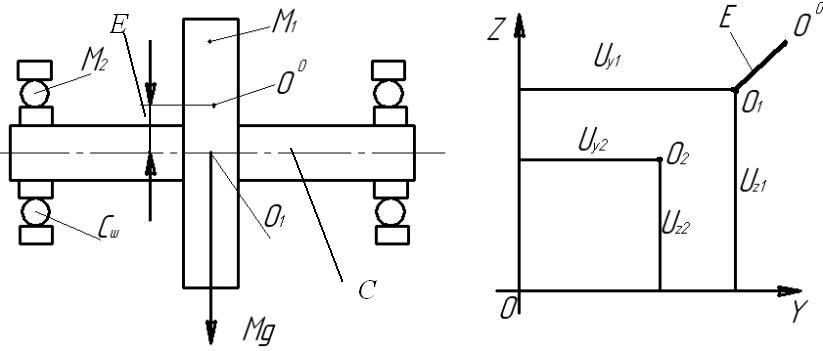
Рисунок 1 – Схема симметричного идеально уравновешенного статически нагруженного ротора с одним диском, опирающегося на два одинаковых подшипника

Задача характеризуется безразмерными параметрами (рис. 1)

ψ = M₁ ∙ g ∙ h² / C³ = 16/27 (C_м /C)³; ν = h ∙ V ∙ E / C; μ = M₂ / M₁;

f = ∆ / E; H = P / √C ∙ M ; λ = r ∙ E² / √C ∙ M ; β = ω / Ω; Ω = √C ∙ M .

Параметр ψ определяет соотношение между жесткостью подшипника качения при статической нагрузке W = ½ M₁ ∙ g и жесткостью ротора.

Параметр ν характеризует влияние неуравновешенности.

Параметр χ характеризует относительный зазор в подшипнике.

Параметр ∆ характеризует средний радиальный зазор между наружным и внутренним кольцами подшипника и телами качения.

Выводы

В отличие от линейной задачи расположение резонансных пиков, которые определяют истинные критические скорости и зависят главным образом от нагруженности подшипника (от параметра ψ) и относительного

зазора в подшипнике χ, влияют и другие составляющие. При этом для малых значений параметра ψ критические скорости могут быть значительно меньше

собственной частоты ротора на абсолютно жестких опорах (β_∞=1). Увеличение зазоров в подшипнике также понижает критические скорости, в этом случае резонансный пик раздваивается и имеет четко выраженный резонанс, как в вертикальном, так и в горизонтальном направлениях, причем резонанс в горизонтальном направлении наступает при меньших скоростях, чем в вертикальном.

При квазистатическом подходе (рис. 1) учитывается лишь влияние статической нагрузки на жесткость подшипников, поэтому такой подход оценки критических скоростей полезен только при незначительных зазорах в подшипниках.

Для тяжелонагруженных роторов влияние неуравновешенности ротора (параметр ν) на характер колебаний невелико, а для малонагруженных – становится определяющим. Уменьшение параметра ν (рис. 1) приводит к существенному смещению резонансных пиков в сторону меньших скоростей. Величина и характер сил демпфирования определяют не только уровень колебаний при резонансе, но и положение резонансных пиков, т.е. значение критических скоростей.

Расчеты показали, что в отличие от линейных систем только линейное трение не ограничивает амплитуд при резонансе, что косвенно подтверждает существование в реальных системах нелинейного трения. Величина параметра χ существенно влияет на вид амплитудных кривых.