Пример повышения точности измерения цифровых весов
Рассмотрим возможности предложенного подхода на примере повышения точности цифровых весов с диапазоном взвешивания 0...100 кгс. Датчик весов емкостного типа с автономным питанием от переносного источника напряжения. Весы предназначены для эксплуатации в диапазоне температуры окружающей среды (воздуха) 0...60°С. Напряжение от автономного источника напряжения в процессе эксплуатации весов может изменяться в диапазоне 12,3...11,7 В при расчетном (номинальном) значении 12 В.
Предварительное исследование цифровых весов показало, что изменения температуры окружающей среды и питаемого напряжения в вышеприведенных диапазонах сравнительно мало влияют на показания емкостного датчика и, следовательно, на результаты взвешивания. Однако стабилизировать эти внешние и внутренние условия с необходимой точностью и поддерживать их в процессе функционирования весов не представлялось возможным ввиду того, что весы должны эксплуатироваться не в стационарных (лабораторных) условиях, а на борту перемещающегося объекта.
Исследование точности весов без учета влияния изменений температуры и питаемого напряжения показали, что средняя абсолютная погрешность аппроксимации составляет 0,16%, а среднеквадратичная погрешность остатка (в единицах измерения выходной величины взвешивания) равна 53,92.
Для получения многофакторной математической модели были приняты следующие обозначения факторов и значения их уровней.
X1 – гистерезис. Уровни: 0 (нагрузка); 1 (разгрузка). Фактор качественный.
X2 – температура окружающей среды. Уровни: 0; 22; 60°C.
X3 – напряжение питания. Уровни:11,7; 12,0; 12,3 В.
X4 – измеряемый вес. Уровни: 0; 20; 40; 60; 80; 100 кгс.
Учитывая принятые уровни варьирования факторов и сравнительно не трудоемкий объем испытаний было решено провести полный факторный эксперимент, т.е. 2 · 32 · 6//108. Исходные данные испытаний были предоставлены проф. П.В. Новицким. Каждый опыт был повторен только один раз, что нельзя признать хорошим решением. Желательно повторение каждого опыта два раза. Предварительный анализ исходных данных показал, что они со значительной вероятностью содержат грубые ошибки. Эти опыты были повторены и их результаты были исправлены.Натуральные значения уровней варьирования факторов были преобразованы в ортогональные контрасты, иначе в систему ортогональных полиномов Чебышева.
С использованием системы ортогональных контрастов структура полного факторного эксперимента будет иметь следующий вид:
(1 + x1) (1 + x2 + z2) (1 + x3 + z3) (1 + x4 + z4 + u4 + v4 + ω4) → N108
где x1,..., x4; z2,..., z4; u4, v4, ω4 – соответственно линейные, квадратичные, кубический, четвертой и пятой степени контрасты факторов X1,..., X4;
N108 – число структурных элементов для схемы полного факторного эксперимента.
Все эффекты (главные и взаимодействия) были нормированы
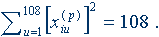
где xiu(p) – значение p-го ортогонального контраста i-го фактора для u-й строки матрицы планирования, 1 ≤ u ≤ 108, 1 ≤ p ≤ si – 1; 1 ≤ i ≤ 4.
Предварительный расчет математической модели показал, что в качестве оценки дисперсии воспроизводимости может быть выбрана (приближенно) величина 20,1.
Число степеней свободы (условно) принято V2 = 108.
Дисперсия была использована для определения стандартной ошибки коэффициентов уравнения регрессии.
Вычисление математической модели и всех ее критериев качества было проведено с использованием ПС ПРИАМ. Полученная математическая модель имеет вид
| ŷ = 28968,9 – 3715,13x4 + 45,2083x3 – 37,5229z2 + 23,1658x2 – 19,0708z4 – 19,6574z3 – 9,0094x2z3 – 9,27434z2x4 + 1,43465x1x2 + 1,65431z2x3, | (2) |
где:
x1 = 2 (X1 – 0,5);
x2 = 0,0306122 (X2 – 27,3333);
z2 = 1,96006 (x22 – 0,237337x2 – 0,575594);
x3 = 3.33333 (X3 – 12);
z3 = 1,5 (x23 – 0,666667);
x4 = 0,02 (X4 – 50);
z4 = 1,875 (x24 – 0,466667);
u4 = 3,72024 (x34 – 0,808x4);
v4 = 7,59549 (x44 – 1,08571x24 + 0,1296).
Дата добавления: 2015-05-28; просмотров: 812;
