Предмет теории принятия решений, основные термины и определения

Введение в теорию принятия решений

Предмет теории принятия решений, основные термины и определения

Теория принятия решений (ТПР) – это совокупность математических дисциплин, в которых исследуются лишь вполне четко описанные и формализованные модели выбора решений при тех или иных начальных условиях, ограничениях на выбор и возможности выбора.

Таким образом, предметом ТПР является изучение процессов, направленных на принятие решений, и способов их формализации.

Под принятием решений будем понимать человеческую деятельность, направленную на выбор наилучшего варианта действий в определенной ситуации [4].

Пусть имеется некоторая система. В ней выделена управляемая подсистема (объект управления) и управляющая подсистема. Сама система находится в некоторой среде (Рис. 1.1).

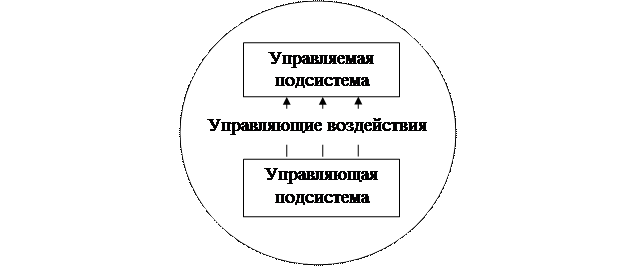
Рис. 1.1. Принятие решений как процесс управления

Управляющая подсистема может воздействовать на объект управления с помощью того или иного управляющего действия, в результате чего объект управления переходит в новое состояние.

Возможные варианты управляющих действий называются альтернативами или решениями.

Целью управляющего действия является перевод объекта управления в наиболее предпочтительное для управляющей подсистемы состояние. Новое состояние объекта определяется двумя факторами: выбранным управляющим действием и состоянием среды.

Важно то, что управляющая подсистема не может воздействовать на среду и, возможно, даже не имеет информации о состоянии среды.

Выбор управляющей подсистемой конкретного управляющего действия (по-другому, альтернативы или решения) называется принятием решения.

Целью принятия решения является нахождение оптимального решения, то есть решения, которое по тем или иным признакам предпочтительные перед другими.

Участника процесса принятия решения называют лицом, принимающим решение (ЛПР).

В процессе принятия решений может принимать участие одно или несколько ЛПР.

Итак, для описания ситуации, в которой происходит принятие решения, необходимо задать три множества:

A – множество альтернатив или управляющих действий,

B – множество состояний среды,

C – множество возможных исходов.

Под термином «исходы» понимаются состояния, в которые может перейти управляемая подсистема.

Так как состояние управляемой подсистемы определяется выбором управляющего действия и состоянием среды, то каждой паре (a, b), где 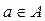, , 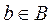соответствует определенный исход 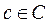. Это означает, что существует функция 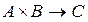. Назовем ее реализационной функцией и обозначим F.

Кроме того, для принятия решения каждый исход необходимо оценить с точки зрения лица, принимающего решение, то есть сформулировать еще и оценочную систему. Для оценки исходов может использоваться:

­ отношение предпочтения исходов;

­ обобщенный критерий (например, функции полезности, эффективности, ценности);

­ разбиение множества исходов C на классы (например, класс «плохих» и «хороших» исходов) и др.

Важно то, что оценивание исходов носит субъективный характер, так как оно производится с точки зрения ЛПР.

Таким образом, построение математической модели задачи принятия решений сводится к заданию множеств A, B, C, реализационной функции F и оценочной системы (в виде функции полезности, отношений предпочтения и т.д.) [11, с. 11 – 14].