Переходная матрица состояния
Пусть линейная САУ описывается уравнениями состояния:
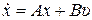 ,
, 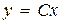 ,
, 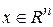 ,
, 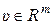 ,
, 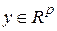 . (8.27)
. (8.27)
Рассмотрим матричный ряд, который обозначим через 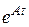 :
:
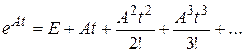 , (8.28)
, (8.28)
где Е – единичная 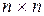 матрица.
матрица.
Доказано, что этот ряд абсолютно сходится при любом t к некоторой 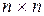 матрице, обозначенной нами через
матрице, обозначенной нами через 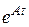 (экспоненциал матрицы).
(экспоненциал матрицы).
Свойства ряда (8.28):
1. При 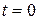 матрица
матрица 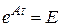 .
.
2. 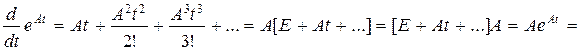
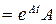 , или в более общем виде
, или в более общем виде 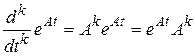 .
.
3. 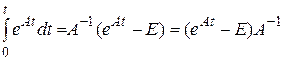 , где
, где 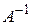 – обратная матрица.
– обратная матрица.
4. Если 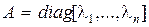 , то
, то 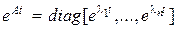 .
.
Рассмотрим однородное уравнение
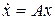 , (8.29)
, (8.29)
соответствующее неоднородному дифференциальному уравнению 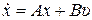 , и зададим начальное состояние вектора х(0) при t = 0.
, и зададим начальное состояние вектора х(0) при t = 0.
Общее решение однородного уравнения (8.29) задается выражением
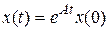 . (8.30)
. (8.30)
Действительно, подставляя (8.30) в (8.29), с учетом свойства 2 получим тождество, справедливое при любом начальном значении х(0). Это значит, что (8.30) определяет общее решение уравнения (8.29).
Введем обозначение 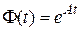 . Матрицу
. Матрицу  размерностью
размерностью 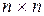 будем называть переходной матрицей состояния (в математике ей соответствует фундаментальная матрица), а выражение (8.30) в этом случае будем записывать в виде
будем называть переходной матрицей состояния (в математике ей соответствует фундаментальная матрица), а выражение (8.30) в этом случае будем записывать в виде
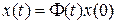 . (8.31)
. (8.31)
Выражение (8.31) можно трактовать как линейное преобразование (переход) начального значения вектора состояния х(0) в текущее значение x(t) в пространстве состояний.
Свойства переходной матрицы состояния:
1. 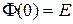 .
.
2. 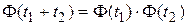 .
.
3. 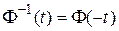 .
.
Эти свойства следуют из общих свойств экспоненциала матрицы.
Если известна переходная матрица состояния, то общее решение неоднородного уравнения 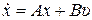 записывается в виде (формула Коши)
записывается в виде (формула Коши)
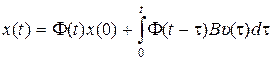 . (8.32)
. (8.32)
В силу 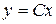 получим выражение для вычисления вектора выхода y(t):
получим выражение для вычисления вектора выхода y(t):
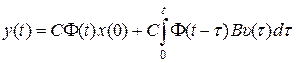 . (8.33)
. (8.33)
В (8.32), (8.33) первое слагаемое определяет свободную составляющую, обусловленную ненулевым начальным состоянием х(0), а второе – вынужденную составляющую, обусловленную входным сигналом 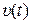 .
.
Выражение (8.28) редко употребляется для определения матрицы  , так как в случае произвольной матрицы А элементы матрицы
, так как в случае произвольной матрицы А элементы матрицы  представляют собой ряды Тейлора при t = 0, пo которым трудно найти исходную функцию в замкнутой форме.
представляют собой ряды Тейлора при t = 0, пo которым трудно найти исходную функцию в замкнутой форме.
Переходную матрицу состояния обычно находят с помощью операционного исчисления. Применим к (8.29) преобразование Лапласа, тогда получим 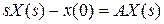 , где
, где 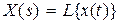 . Из полученного выражения находим
. Из полученного выражения находим 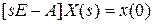 ,
, 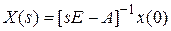 , где
, где 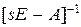 – обратная матрица к матрице
– обратная матрица к матрице  .
.
Переходя к оригиналам, имеем
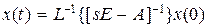 . (8.34)
. (8.34)
Сравнивая (8.34) с (8.31), приходим к выводу, что
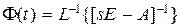 . (8.35)
. (8.35)
Каждый элемент матрицы 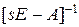 есть дробно-рациональная функция переменной s. Знаменатель каждого элемента представляет собой полином n-й степени
есть дробно-рациональная функция переменной s. Знаменатель каждого элемента представляет собой полином n-й степени 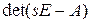 , а числитель – полином не выше (n – 1)-й степени. Полином
, а числитель – полином не выше (n – 1)-й степени. Полином 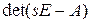 называется характеристическим полиномом системы, а алгебраическое уравнение n-й степени
называется характеристическим полиномом системы, а алгебраическое уравнение n-й степени
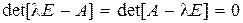 (8.36)
(8.36)
назовем характеристическим уравнением системы.
Применяя к каждому элементу матрицы 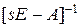 обратное преобразование Лапласа, получим матрицу
обратное преобразование Лапласа, получим матрицу  , элементами которой будут некоторые функции времени.
, элементами которой будут некоторые функции времени.
Переходную матрицу состояний можно найти, используя модальную матрицу M. Пусть в уравнении (8.29) матрица А имеет различные собственные значения 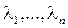 . Тогда в (8.29) сделаем замену переменных
. Тогда в (8.29) сделаем замену переменных 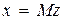 , где М – модальная матрица. В результате получим:
, где М – модальная матрица. В результате получим:  .
.
Общее решение полученной системы с диагональной матрицей будет таково: 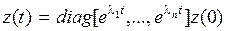 . Так как
. Так как  ,
, 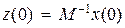 , то общее решение исходного уравнения (8.29) запишется в виде
, то общее решение исходного уравнения (8.29) запишется в виде 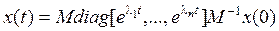 .
.
Отсюда следует, что
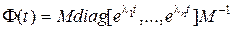 . (8.37)
. (8.37)
Пример 8.7. Рассмотрим однородное уравнение в нормальной форме:
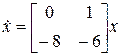 .
.
Собственные числа матрицы А определяются из решения уравнения 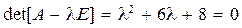 и будут
и будут  ,
, 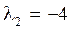 .
.
Ищем модальную матрицу М в виде (8.14):
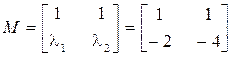 ,
, 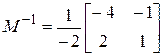 .
.
Находим  в соответствии с (8.37):
в соответствии с (8.37):
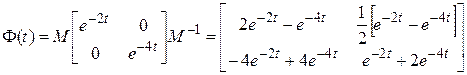 .
.
Можно найти  , используя (8.35). Находим
, используя (8.35). Находим  и затем
и затем 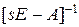 .
.
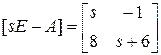 ,
, 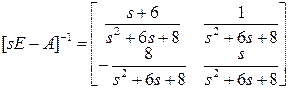 .
.
Переходя от  к оригиналам, найдем выражение для матрицы
к оригиналам, найдем выражение для матрицы  , не отличающееся от полученного ранее.
, не отличающееся от полученного ранее.
Дата добавления: 2015-05-26; просмотров: 778;
