Оператор условного перехода

Разветвляющийся вычислительный процесс, содержащий две ветви, схематично может быть изображен с помощью структуры выбора (структуры разветвления), которая содержит три элемента: логическое условие, ветвь ДА и ветвь НЕТ. Общий вид структуры представлен на рис.1.

После вычислений, общих для обеих ветвей (блок 1), проверяется некоторое условие (блок 2). Если оно выполняется, то осуществляется переход к первой ветви – ветви ДА (блок 3), в противном случае – ко второй ветви – ветви НЕТ (блок 4). После выполнения вычислений в любой из ветвей осуществляется переход к общему участку 2 (блок 5). Структура выбора в языке Паскаль реализуется с помощью условного оператора (оператора условного перехода), который позволяет выполнять один из двух входящих в него операторов в зависимости от значения некоторого логического выражения. Оператор имеет следующий вид:

ΙF < логическое выражение >

THEN < оператор 1 >

ELSE < оператор 2 >; где IF (если), THEN (то), ELSE (иначе) – служебные слова; оператор 1, оператор 2 – любые операторы языка.

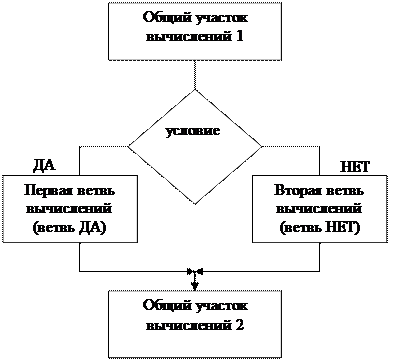
Рис.1.

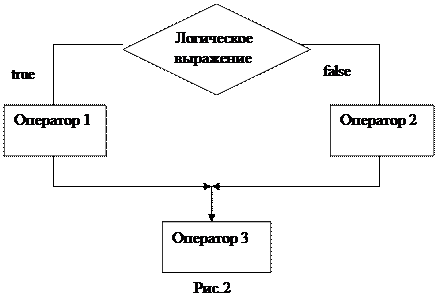
Порядок выполнения условного оператора поясняется рис. 2. Если значение логического выражения равно true (истинно), то выполняется оператор 1 (оператор 2 пропускается), если значение логического выражения равно false (ложно), то выполняется оператор 2 (оператор 1 пропускается). Далее в любом случае выполняется оператор, стоящий в программе непосредственно за оператором if (оператор 3).

Значение true и false получают обычно в результате выполнения операций сравнения (отношения):

<- меньше;

<=- меньше или равно;

> - больше;

>= - больше или равно;

= - равно;

< > - не равно.

Операнды этих операций (константы, переменные, функции, выражения, не содержащие отношений) могут быть вещественного, целого или логического типа.

Простейшим примером использования условного оператора является вычисление значения функции по одной из двух предложенных формул в зависимости от значения аргумента:

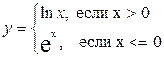
Оператор, реализующий выражение для некоторого значения аргумента Х, выглядит следующим образом:

IF X>0

THEN Y: =LN (X)

ELSE Y: =EXP (X);

Здесь логическое выражение – отношение Х>0, оператор 1, оператор 2 – операторы присвоения Y: =LN (X) и Y: =EXP (X).

Примером, когда логическое выражение в операторе имеет более сложную структуру, может служить задача определения, можно ли построить треугольник из отрезков заданной длины: x,y,z (x>0, y>0, z>0).

Условный оператор имеет вид:

IF (X+Y>Z) AND (X+Z>Y) AND (Y+Z>X)

THEN WRITELN (‘треугольник построить нельзя’);

ELSE WRITELN (‘треугольник построить нельзя’);

Условный оператор может не иметь конструкции ELSE, такая форма оператора называется сокращенной:

IF <логическое выражение> THEN <оператор>;

Порядок выполнения оператора IF в сокращенной форме поясняется рис. 3.

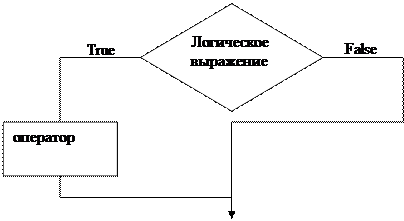Рис. 3

Если логическое выражение принимает значение FALSE , то сразу выполняется оператор, следующий за оператором IF.

Например,

IF X>0 THEN WRITELN (X);

Z: =SQR (X);

Условные операторы могут иметь вложенную конструкцию, когда после THEN или FALSE используется так же условный оператор. При этом справедливо следующее правило: ELSE всегда относится к ближайшему слева оператору IF. Например, требуется вычислить значение функции по одной из предложенных форму:

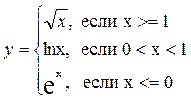
Для программной реализации используется вложенная конфигурация условного оператора:

IF X>=1

THEN Y: =SQRT (X)

ELSE IF X>0

THEN Y: =LN (X)

ELSE Y: =EXP (X);

В состав условного оператора может входить только один оператор. Если какую либо ветвь разветвления требуется вставить несколько операторов, то они объединяются в один, составной оператор, для чего в начале группы этих операторов записывается слово BEGIN, а в конце – служебное слово END:

BEGIN

<оператор 1>;

<оператор 2>;

……………..

<оператор N>;

END;

Элементами составного оператора могут быть любые операторы языка, в том числе условные и другие составные операторы.

Пример: Вычислить корни квадратного уравнения общего вида а <>0, ax²+bx+c=0 в области действительных чисел. Введем следующие обозначения: A, B, C – коэффициенты уравнения;

D – дискриминант;

X1, X2 – корни;

E – допустимая погрешность вычислений.

{ОПРЕДЕЛЕНИЕ КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ}

PROGRAM KU;

CONST

E=1E-4; {погрешность вычислений}

VAR

A, B, C, X1, X2, D: REAL;

BEGIN

READ (A, B, C);

WRITELN (‘A=’, A,’B=’, B,’C=’, C);

D: =SQR (B)-4*A*C;

IF D <0

THEN WRITELN (‘корни мнимые’)

ELSE BEGIN

IF ABS (D)<E

THEN BEGIN

X1: =-B/(2*A);

X2: =X1;

END

ELSE BEGIN

X1: =(-B+SQRT (D))/(2*A);

X2: =(-B-SQRT (D))/(2*A);

END;

WRITELN (‘X1=’, X1, ’X2=’, X2);

END;

END.

Для каждого условного оператора конструкции THEN, ELSE записаны под соответствующим IF; операторы, ограниченные операторными скобками BEGIN – END, записаны так же друг под другом и смещены вправо относительно BEGIN и END.

В примере структура выбора входит составной частью в одну из ветвей (ветвь - НЕТ) другой структуры выбора, такие ветвления называются сложными.

Оператор варианта.

Оператор варианта является обобщением условного оператора: он дает возможность выполнить один из нескольких операторов в зависимости от значения некоторого выражения, называемого селектором. В общем случае оператор имеет вид:

CASE <селектор> OF

<список меток 1>: <оператор 1 >;

<список меток 2>: <оператор 2 >;

…………………………………………….

<список меток N>: <оператор N >;

END;

Где CASE (выбор), OF(из), END(конец) – служебные слова;

Селектор – выражение любого скалярного типа, кроме вещественного;

Оператор – любой оператор языка, в том числе и составной;

Список меток – список разделенных запятыми значений выражения селектор или одно его значение. Эти константы, следовательно, должны иметь тот же тип, что и селектор, и называются они метками варианта. Метка варианта – не обычная метка: это не обязательно целое число, она не описывается в разделе LABEL, на нее нельзя ссылаться в операторе GOTO.

Оператор варианта выбирает для исполнения тот оператор, одна из меток которого равна текущему значению выражения селектор. По окончании выполнения выбранного оператора управление передается в конец оператора CASE.

Метки полей не должны пересекаться. Если ни одна метка не найдена, то управление передается за оператор END.

Можно использовать следующую конструкцию:

CASE I OF

1 : <оператор 1>;

2 : <оператор 2>;

ELSE <оператор 3>; END;

Рассмотрим оператор на примере:

CASE NOMER OF

0 : y: =G;

1..3 : y: =G*X;

6,7,8 : y: =G*sqrt (abs (x));

9..11 : y: =G*exp (x)+H;

12 : y: =G*sqr (sin (x)+H);

END;

В зависимости от значения селектора NOMER значение функции У вычисляется по одной из перечисленных формул. Схематическое представление оператора CASE – структура отбора, представлена для данного примера на рис.4.

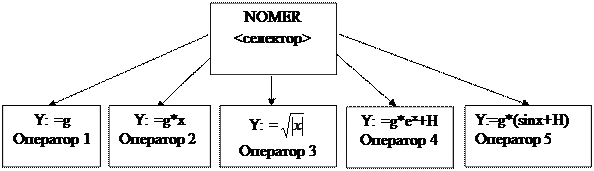Рис. 4

Метка может быть константой, диапазоном констант и списком:

0 и 12 – константа;

1..3 и 9..11 – диапазон констант;

6,7,8 – список констант.

Такие вычисления могут быть выполнены и с помощью вложенных условных операторов, однако это в значительной степени удлинило бы программу и сделало бы ее менее наглядной.

Пример: Найдем остаток от деления значения целого выражения С=К*(А+В) на 4 и выведем сообщение о величине остатка. Если остаток равен 0, то значение переменной С оставим без изменения, если 1 или 3 – уменьшим на величину остатка, если 2 – увеличим на величину остатка. Новое значение С так же выведем на печать (оно делится на 4 нацело).

Программа решения имеет вид

{ОПРЕДЕЛЕНИЕ ОСТАТКА}

PROGRAM OSTATOK;

CONST

DEL=4;

VAR A, B, C, K: INTEGER;

OST: 0..3;

BEGIN {OSTATOK}

READ (A, B, K);

WRITELN (‘A=’, A,’B=‘, B,’K=’, K);

C: =K*(A+B);

OST: =C MOD DEL;

CASE OST OF

0: WRITELN (‘ОСТАТОК 0’);

2: BEGIN

WRITELN (‘ОСТАТОК 2’);

C: =C+OST

END;

1,3: BEGIN

WRITELN (‘ОСТАТОК 1,3’);

C: =C-OST

END;

END {CASE}

END.

Введены дополнительные обозначения: константа DEL – делитель, равный 4, OST – величина остатка, описанная как переменная ограниченного целого типа с диапазоном от 0 до 3.

Далее составной оператор или операторные скобки с комментарием {остаток}, вводятся переменные А,В,К и выводятся. Вычисляется переменная С и OST от деления С на DEL. По оператору варианта происходит выбор остатка, если OST =0, то выводится результат – остаток 0, если OST=2, то новые операторные скобки, выводится остаток 2 и величина С увеличивается на величину OST, OST=1 или 3 – новые операторные скобки, вKЀводится остаток 1, 3 и величина С уменьшается на величину OST.