Вложенные циклы.
Если телом цикла является циклическая структура, то такие циклы называют вложенными или сложными. Цикл, содержащий в себе другой цикл, называют внешним. Цикл, содержащийся в теле другого цикла, называют внутренним. Внутренний и внешний цикл могут быть любыми из трёх рассмотренных видов: цикл с параметром, цикл с предусловием, цикл с постусловием. Правила организации как внешнего, так и внутреннего циклов такие же, как и для простого цикла каждого из этих видов. Однако при построении вложенных циклов необходимо соблюдать следующее условие: все операторы внутреннего цикла должны полностью лежать в теле внешнего цикла. Сложные циклы условно разбивают на уровни вложенности. На рис. 5 представлена структура вложенных циклов с параметром, для которой: внешний цикл 1 имеет уровень 0, внутренний цикл 2 – уровень 1, внутренний цикл 3 – уровень 2. Цикл 2 является внешним по отношению к циклу 3 и внутренним по отношению к циклу 1.
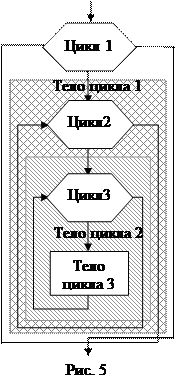 Параметры циклов разных уровней изменяются не одновременно. Вначале все свои значения изменит параметр цикла наивысшего уровня вложенности при фиксированных (начальных) значениях параметров циклов с меньшим уровнем (на рис. 5 это цикл 3). Затем изменяется на один шаг значение параметра цикла следующего уровня (цикл 2) и снова полностью выполняется самый внутренний цикл и т. д. до тех пор, пока параметры циклов всех уровней не примут все требуемые значения.
Параметры циклов разных уровней изменяются не одновременно. Вначале все свои значения изменит параметр цикла наивысшего уровня вложенности при фиксированных (начальных) значениях параметров циклов с меньшим уровнем (на рис. 5 это цикл 3). Затем изменяется на один шаг значение параметра цикла следующего уровня (цикл 2) и снова полностью выполняется самый внутренний цикл и т. д. до тех пор, пока параметры циклов всех уровней не примут все требуемые значения. 
Пример: Вычислить значение функции 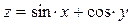 при x изменяющемуся от
при x изменяющемуся от
x0 до xn с шагом hx и y изменяющемся от y0 до yn с шагом hy.
Аргументы функции x и y – вещественные числа.
Так как параметром цикла не может быть переменная вещественного типа, то необходимо введение двух дополнительных целых переменных i и j , которые будут являться счетчиками значений переменных x и y. Число повторений внешнего и внутреннего циклов определим следующим образом:
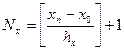
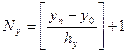
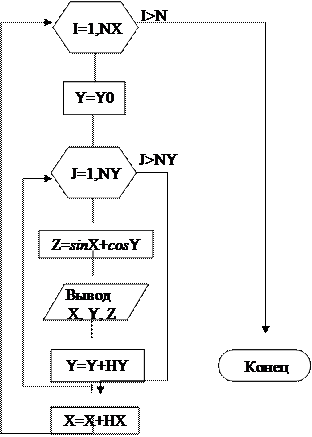
Блок-схема задачи приведена на рис. 6.
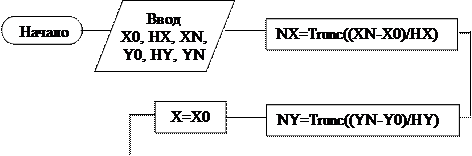 | |||||
 | |||||
|
Программа имеет вид:
PROGRAM TABUL;
VAR
I, J, NX, NY: INTEGER;
X, X0, Y0, HX, XN, Y, HY, YN: REAL;
BEGIN
READ (X0, HX, XN, Y0, HY, YN);
NX: = TRUNG ((XN-X0)/HX)+1;
NY: = TRUNG ((YN-Y0)/HY)+1;
X: =X0;
FOR I: =1TO NX DO
BEGIN {НАЧАЛО ВНЕШНЕГО ЦИКЛА}
Y: = Y0;
FOR J: =1 TO NY DO
BEGIN {НАЧАЛО ВНУТРЕННЕГО ЦИКЛА}
Z: = SIN(X)+COS(Y);
WRITELN (‘X=’, X, ‘Y=’, Y,’Z=’, Z);
Y: =Y+HY;
END; {КОНЕЦ ВНУТРЕННЕГО ЦИКЛА}
X: =X+HX
END; {КОНЕЦ ВНЕШНЕГО ЦИКЛА}
END. {TABUL}
В блоке 2 осуществляется ввод значений x0, hx, xn, y0, hy, yn. В блоках 3 и 4 вычисляется число повторений nx и ny и с помощью функции TRUNC происходит выделение целой части числа.
В блоке5 задается начальное значение аргумента X=0. В блоке 6 параметру внешнего цикла задается начальное значение I=1, после чего происходит сравнение значения NX. При I<=NX управление передается блоку 7, где вычисляется начальное значение аргумента Y. В блоке 8 параметру внутреннего цикла задается начальное значение J=I, после чего происходит сравнение значения параметра цикла с конечным значением NX.
При J<=NY управление передается блоку 9,где происходит вычисление значения функции Z. В блоке 10 полученные значения X, Y, Z выводятся на экран. В блоке 11 значение переменной Y увеличивается на величину шага HY, после чего происходит возврат к блоку 8, где параметр цикла J получает следующее значение. Вычислительный процесс повторяется до тех пор, пока значение параметра цикла J не превысит конечное значение NY, после чего управление передается блоку 12. В блоке 12 значение переменной Х увеличивается на величину шага НХ, после чего происходит возврат к блоку 6, где параметр внешнего цикла J получает следующее значение. При J<=NX управление снова передается блоку 13 и программа завершает свою работу.
Дата добавления: 2015-04-05; просмотров: 2354;
