Операторы цикла с присваиванием.
Различают циклы с заданным и заранее неизвестным числом повторений. Циклы первого типа называют также циклами со счетчиком. Число повторений тела цикла в этом случае подсчитывается с помощью специальной переменной (счетчика), для которой известны начальное и конечное значения, шаг её изменения. Управление циклом осуществляется на основании сравнения текущего значения счетчика с конечным. Переменную – счетчик именуют параметром цикла, а сам цикл – циклом с параметром.
Оператор цикла с параметром имеет следующий вид:
For i:=m1 to m2 do s или
For i:=m1 down to m2 do s
Где for (для), To (до), Downto (вниз до), Do(выполнить) – служебные слова;
I – параметр цикла (переменная любого скалярного типа, кроме вещественного);
M1, m2 – начальное и конечное значения параметра цикла (тип, который должен совпадать с типом параметра цикла);
S – тело цикла, которое может содержать один или несколько операторов.
Работа оператора цикла при использовании служебного слова To заключается в следующем. Параметр цикла принимает начальное значение (m1) и сравнивается с конечным значением (m2). Если параметр цикла не превышает значения m2, то управление передаётся в тело цикла и операторы выполняются. Затем значение параметра цикла увеличивается на единицу, и работа повторяется. Выход из цикла выполнится после того, как значение параметра цикла превысит конечное значение m2.
При использовании в операторе цикла служебного слова Downto параметр цикла будет изменяться в обратном порядке: с шагом – 1.
Для схематического представления цикла с параметром используют специальный блок заголовка цикла (блок модификации), внутри которого указывают закон изменения параметра цикла. Схематическая запись циклического алгоритма в этом случае показана на рис.1.
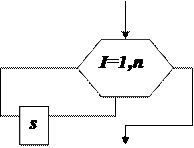
Рис.1.
На схеме вход 1 в блок модификации – первоначальный вход в цикл, вход 2 – вход в цикл при его очередном повторении, выход 3 – из цикла по его окончании.
Оператор цикла for следует использовать во всех случаях, когда заранее известно число повторений или его можно подсчитать. Число повторений n можно подсчитать при изменении аргумента с постоянным шагом h в определённом интервале (от начального xn до конечного xk значения) по следующей формуле:
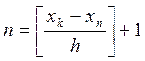
Квадратные скобки указывают на то, что результат округляется до целой части путём отбрасывания дробной.
Пример: Составить программу для вычисления и вывода значений функции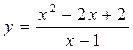 
при изменении x от –4 до 4 с шагом 0,2.
Подсчитаем число повторений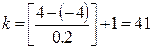 
Блок-схема алгоритма функции y приведена на рис.2.
PROGRAM FUNY;
VAR X, Y: REAL;
K: INTEGER;
BEGIN
X: =-4;
FOR K: = 1 TO 41 DO
BEGIN {НАЧАЛО ЦИКЛА}
Y: =(X*X-2*X+2)/(X-1);
WRITE (X, Y);
X: = X+0,2
END {КОНЕЦ ЦИКЛА}
END.
В блоке 2 переменная x получает начальное значение равное –4. В блоке 3 параметру цикла задается начальное значение k =1, после чего происходит сравнение значения параметра цикла с конечным значением равным 41. При k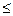 
41 управление передается блоку 4, где происходит вычисление переменной y . В блоке 5 происходит вывод на экран значений переменных x и y. В блоке 6 значение переменной увеличивается на величину шага равного 0,2. После чего происходит возврат к блоку 3, где параметр цикла x получает следующее значение. Вычислительный процесс повторяется до тех пор, пока значение параметра цикла не станет равным 42, после чего управление передаётся блоку 7.
Рис.2
При программировании циклов с параметрами необходимо помнить следующие правила организации цикла:
1) параметры цикла, начальное и конечное значения, должны быть одинакового типа, их тип может быть любым скалярным типом (стандартным, перечисляемым, ограниченным), кроме вещественного;
2) очередное значение параметра цикла вычисляется автоматически с помощью функции SUCC в сочетании с TO или PRED в сочетании с DOWNTO; в частности для целого типа шаг изменения значения параметра цикла равен 1 при TO и -1 при DOWNTO;
3) запрещено изменять внутри (в теле) цикла значение параметра цикла, начальное и конечное значение;
4) запрещено входить в цикл с помощью оператора GOTO, минуя оператор FOR, так как значение переменной параметра цикла, начальное и конечное значения будут неопределены;
5) цикл не выполняется вообще, если начальное значение больше (при DOWNTO - меньше), чем конечное;
6) по окончанию выполнения цикла значение переменной параметра неопределенно и не может быть использовано в дальнейших вычислениях;
7) после служебного слова DO может стоять только один оператор; если в цикле нужно выполнить группу операторов, то их заключают в операторные скобки BEGIN-END;
8) из составного оператора, входящего в оператор цикла, можно выйти до окончания этого цикла с помощью GOTO, тогда последнее значение параметра цикла сохраняется.
Пример: Вычислить степень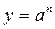 
вещественного числа a с натуральным показателем n. Воспользуемся для вычисления следующей формулой:
Компактно такое произведение может быть записано в виде: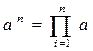 
Для вычисления указанного произведения целесообразно организовать цикл с параметром i, в котором осуществлялось бы постепенное накопление произведения y по следующему правилу: до начала цикла переменная y должна получить значение 1, на каждом шаге цикла (для y =1,2…..,)-y = y·a. Цикл с параметром i будет выполнен n раз.
Программа решения задачи имеет вид:
{ОПРЕДЕЛЕНИЕ СТЕПЕНИ ВЕЩЕСТВ. ЧИСЛА}
PROGRAM STEPEN;
VAR
A, Y: REAL;
I, N: INTEGER;
BEGIN {STEPEN}
READ (A, N);
Y: =1;
FOR I: =1 TO N DO
Y: =Y·A;
WRITELN (N,’СТЕПЕНЬ ЧИСЛА’, A);
WRITELN (‘РАВНА’, Y)
END. {STEPEN}
Вначале осуществляется ввод произвольного значения a и n. Дальше задается начальное значение произведения y = 1. Параметру цикла присваивается значение i =1, после чего происходит сравнение параметра цикла i с конечным значением n. При i≤n управление передается оператору, где происходит процесс последовательного вычисления произведения. При i>n управление передается оператору вывода на экран вычисленного значения произведения.
Пример: Вычислить значение функции
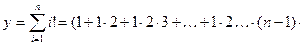n
Члены последовательности, стоящие под знаком суммы можно записать следующим образом:
P1=1! = 1
P2=2! =1·2
P3=3! =1·2·3
P4=4! =1·2·3·4
. . . . . . . . . . . . . . . . . . .
Pn=n! =1·2·3·. . . .·n
Отсюда
P2=P1·2
P3=P2·3
P4=P3·4
PI=PI-1·I
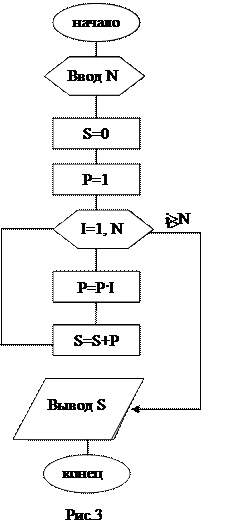
Блок-схема задачи приведена на рис. 3.
Программа имеет вид:
PROGRAM SUM;
VAR
N, I: INTEGER;
S, P: REAL;
BEGIN {SUM}
READ (N);
S: =0;
P: =1;
FOR I: =1 TO N DO
BEGIN {НЦ}
P: =P·I;
S: =S+P;
END; {КЦ}
WRITELN (‘S=’, S)
END. {SUM}
Дата добавления: 2015-04-05; просмотров: 1032;