Теорема сложения вероятностей. Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из них.
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из них.
Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Для несовместных событий:
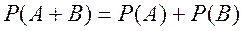 (2.4)
(2.4)
Для совместных событий:
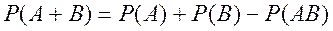 (2.5)
(2.5)
где Р(АВ) –– вероятность появления событий А и В одновременно.
Полной группой нескольких событий называется счетное множество событий, одно из которых непременно произойдет и не существует событий, выходящих за пределы рассматриваемого множества.
Если события Al…..An несовместны и образуют полную группу событий, то:
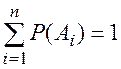 (2.6)
(2.6)
Сумма вероятностей противоположных событий равна 1:
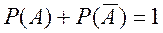 (2.7)
(2.7)
где 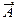 –– событие, противоположное событию А.
–– событие, противоположное событию А.
Условной вероятностью события A при наличии события B называется вероятность события A, вычисленная при условии, что событие B произошло. Эта вероятность обозначается 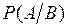 .
.
События A и B называются независимыми, если появление одного из них не меняет вероятность появления другого.
Для независимых событий
 (2.8)
(2.8)
Теорема умножения вероятностей.
Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого.
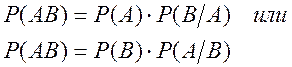 (2.9)
(2.9)
Для независимых событий:
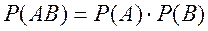 (2.10)
(2.10)
Задача 2.5.
Партия изделий состоит из a исправных и b неисправных. Выбирается одно изделие, проверяется на исправность и возвращается в эксперимент. После этого из партии берется еще одно изделие.
Найти вероятность того, что оба изделия будут исправными.
Ответ.
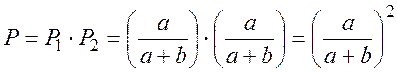
Дата добавления: 2015-05-26; просмотров: 1197;
