Задача 2.1.
Некоторые характеристики случайных величин, событий, процессов в оценках надежности технических систем
Основные понятия, непосредственный подсчет вероятностей.
Если в результате опыта из общего числа случаев n число благоприятных для события A случаев составляет m, то вероятность реализации события A вычисляется по формуле:
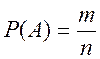 (2.1)
(2.1)
В теории надежности большую роль играет так называемая схема Бернулли. Предположим, что производится последовательно n испытаний, в каждом из которых событие А может произойти с одной и той же вероятностью р. Спрашивается, чему равна вероятность того, что событие А реализуется при m испытаниях, а при n-m испытаниях –– событие не произойдет.
Если обозначить эту вероятность через 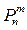 , и принять q=1-p, то имеет место формула Бернулли:
, и принять q=1-p, то имеет место формула Бернулли:
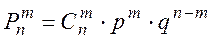 (2.2)
(2.2)
где  –– число сочетаний из n элементов по m.
–– число сочетаний из n элементов по m.
Наряду с формулой Бернулли значительную роль играет схема, именуемая схемой невозвращенного шара. Если имеется N предметов, среди которых М обладают определенным отличием А, а остальные этим свойством не обладают, то при выборе n единиц наудачу из N предметов, вероятность того, что среди выбранных n предметов m будут отличаться свойством А, определяется формулой:
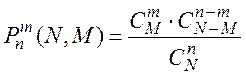 (2.3)
(2.3)
Задача 2.1.
Среди поставленных на испытания изделий имеются a исправных и b неисправных, (a³2).
Найти вероятность того, что взятые наугад два изделия окажутся исправными.
Решение.
Общее число возможных случаев 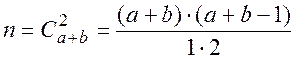
Число благоприятных случаев 
Вероятность события A –– оба изделия исправны:
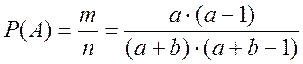
Дата добавления: 2015-05-26; просмотров: 902;
