Непружне розсіювання
Для непружного розсіювання характерним є те, що у результаті взаємодії енергія електрона пучка змінюється, хоча напрям його руху фактично не змінюється (jн << jп, де jн – кут для непружного розсіювання). Існує багато можливих наслідків непружного розсіювання. Коротко зупинимося на деяких основних.
Збудження плазмонів. Електронний пучок може збудити хвилі у “вільному електронному газі”. Це дуже ймовірний процес непружного розсіювання, оскільки для збудження плазмонів потрібно передати енергію 10-20 еВ.
Збудження електронів провідності. Енергія, яка передається від електронного пучка, достатня для забезпечення роботи виходу електрона, що знаходиться у зоні провідності твердого тіла, за поверхню зразка. Такі електрони отримали назву вторинних. Більшість із них має енергію до 50 еВ. Сигнали від вторинних електронів використовуються у растровому електронному мікроскопі.
Iонiзацiя внутрішніх оболонок. Електрони, що мають достатньо високу енергію, при взаємодії з атомами можуть вибити зв’язані електрони, якi знаходяться на внутрішніх оболонках атомів. Це призводить до переведення атомів у збуджений стан. Унаслідок релаксації відбувається випромінювання рентгенівських квантів та оже-електронiв. Сигнали від характеристичного рентгенівського випромінювання використовуються для рентгенівського мікроаналізу, а від оже-електронiв – для аналізу елементного складу твердого тіла.
Гальмівне (безперервне) рентгенівське випромінювання. Електрон пучка з високою енергією може гальмуватися у кулонівському полі атома. Різниця між енергією електрона до i після гальмування виділяється на випромінювання рентгенівського кванта. Таке рентгенівське випромінювання отримало назву гальмівного. Енергія рентгенівських квантів може набувати будь-якого значення від 0 до енергії пучка. З цієї причини дане випромінювання отримало назву безперервного, а спектр, відповідно, – безперервний. Воно не становить цінності як сигнал для мікроскопії та мікроаналізу.
Збудження фононів. Значна частка енергії, яка передається електронами пучка твердому тілу (кристалу), йде на збудження коливань кристалічної решітки (фононів). Іншими словами, енергія йде на нагрівання твердого тіла. У випадку, коли пучок падає на масивну мішень, то ділянка, якій електрони віддають свою енергію, має надійний тепловий контакт із рештою зразка. За рахунок відтоку тепла від місця падіння пучка температура мішені фактично не змінюється. Наприклад, для струмів пучка порядку 1 нА, який падає на масивний зразок, спостерігається підвищення температури приблизно на 10 К. Для пучка зі струмом 1 мкА, або коли зразок достатньо тонкий, має місце істотний нагрів мішені. Нагрів електронним пучком, що має високу густину струму, використовується у технології електронно-променевого випаровування, зварювання та плавлення.
Розрахунок втрати енергії при непружних процесах електроном пучка у твердому тiлi є достатньо складним. Існує ряд теоретичних моделей, що описують цей процес. Найбільше поширення знайшла модель німецького фізика Бете, який на основі квантового підходу отримав вираз для швидкості втрати енергії при проходженні електроном твердої мішені. Співвідношення Бете має такий вигляд:
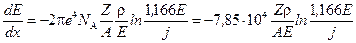 , (1.4)
, (1.4)
де 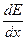 – швидкість втрати енергії, (кеВ/см); Е – середня енергія електрона на шляху (кеВ);
– швидкість втрати енергії, (кеВ/см); Е – середня енергія електрона на шляху (кеВ); 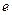 – заряд електрона;
– заряд електрона; 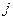 – середній потенціал іонізації; знак “–” вказує на те, що енергія електрона зменшується.
– середній потенціал іонізації; знак “–” вказує на те, що енергія електрона зменшується.
Середній потенціал iонiзацiї показує, яку енергію втрачає електрон за один акт взаємодії, та визначається за формулою
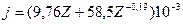 , кеВ. (1.5)
, кеВ. (1.5)
Дана формула враховує всі можливі процеси втрати енергії.
Координата х у спiввiдношеннi (1.4) визначається на прямій лінії вздовж траєкторії руху електрона. Насправді траєкторія електрона відрізняється від прямої лінії. У зв’язку з цим при розрахунку втрати енергії у спiввiдношеннi (1.4) потрібно вводити поправку на зміну траєкторії. Якщо розрахунок втрат енергії ведеться для тонкоплiвкових зразків, то поправку на траєкторію у спiввiдношення Бете не вводять.
Часто спiввiдношення Бете виражають через гальмівну здатність (S)
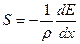 . (1.6)
. (1.6)
Процеси пружного та непружного розсіювання конкурують між собою. За рахунок пружного розсіювання електрон відхиляється від первинного напрямку руху i дифундує в тверде тіло. Непружне розсіювання зменшує енергію електрона доти, поки вона не стане такою, як енергія вільних електронів у кристалі. Зменшення енергії призводить до обмеження області зразка, в яку може проникнути електрон пучка.
Область твердого тіла, де електрони пучка втрачають свою енергію, отримала назву області взаємодії.
Для коректної обробки результатів досліджень за допомогою приладів з електронним зондом потрібно знати форму та розміри області взаємодії, а також залежність їх від параметрів мішені й пучка.
2 Область взаємодії пучка електронів з твердим тілом
Електронним бомбардуванням фоторезистів з подальшим травленням вдалось отримати експериментальні дані про форму та розміри області взаємодії. Так, було встановлено, що область взаємодії (рис. 1.3) має розмір у декілька мікронів з глибиною більшою, ніж ширина. За формою вона подібна до груші,

Рисунок 1.3 – Область взаємодії пучка електронів із фоторезистом
що пов’язано з наступним. На перших стадіях взаємодії більш імовірним є непружне розсіювання (електрон не змінює напряму свого руху). Далі, у мiру його руху, в зразку відбувається втрата енергії i збільшується ймовірність пружного розсіювання. За рахунок пружного розсіювання електрон змінює напрям свого руху, що призводить до розширення області взаємодії.
Для того щоб визначити форму та розміри області взаємодії у мішені, існує спосіб моделювання траєкторії електрона, який отримав назву методу Монте-Карло.
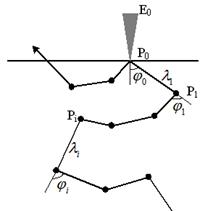
Рисунок 1.4 – Спрощена модель траєкторії руху електронів
При розрахунках методом Монте-Карло вважають, що електрон з енергією Е0 падає на поверхню зразка у деяку точку Р0 (рис. 1.4). Він може пружно або непружно розсіятися або відбитися від зразка. Кожний електрон після акту розсіювання у точці Рi проходить по прямій лінії відстань li. Причому у точці Рi він змінює напрям свого руху на кут ji. Відстань від точки Рi до точки Рi+1 електрон проходить з енергією Еi, яка може бути меншою Еi-1, або дорівнювати цій енергії залежно від виду розсіювання. Середня довжина вільного пробігу визначається за співвідношенням (1.2), а втрата енергії розраховується виходячи із співвідношень теорії Бете. У першому наближенні можна використати співвідношення для середнього потенціалу іонізації.
Значення кутів та типу розсіювання вибирають за допомогою генератора випадкових чисел (метод рулетки). Цей метод забезпечує вибірку значень у заданому інтервалі величин таким чином, щоб створити розподіл актів розсіювання подібним до поведінки реальних систем. Розрахунок проводиться доти, поки величина енергії електрона не зрівняється із значенням енергії вільного електрона у твердому тілі. Кількість траєкторій електронів залежить від того, як швидко буде отриманий статистично правильний результат. Рисунок 1.5 ілюструє типовий результат розрахунку траєкторій для 100 електронів. Відмітимо, що числові значення розміру області взаємодії мають наближений характер, а її розмір нечітко виражений.
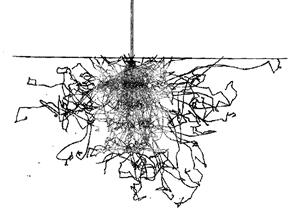
Рисунок 1.5 – Розраховані методом Монте-Карло траєкторії електронів
Дані експериментів та розрахунків показують, що густина втрати енергії непостійна в межах області взаємодії, яка має ядро з високою густиною втрат енергії поблизу місця падіння пучка. Біля краю області взаємодії густина траєкторій електронів зменшується і падає до нуля.
Розглянемо вплив атомного номера мішені на форму та розміри області взаємодії. Розрахунок, проведений методом Монте-Карло для мішеней з різних матеріалів при одній i тій самій енергії пучка, показує, що лiнiйнi розміри області взаємодії зменшуються зі зростанням атомного номера (рис. 1.6). Даний ефект можна пояснити на основі співвідношення (1.3), з якого випливає, що переріз пропорційний Z2. У мішені з високим атомним номером електрони відчувають великі пружні удари, відтак середній кут розсіювання більший, ніж у мішені з малим атомним номером. Траєкторії електронів швидше відхиляються від первинного напряму руху, а глибина проникнення зменшується. У мішені з малим атомним номером траєкторія менше відхиляється від початкового напряму руху, що призводить до більшого проникнення електронів у товщу матеріалу.
Розміри області взаємодії залежать також i від енергії пучка (рис. 1.6). Зі збільшенням E0 розмір області взаємодії збiльшується. Даний ефект можна зрозуміти із аналізу співвідношень (1.3) та (1.4). Як видно з (1.3), ймовірність пружного розсіювання обернено пропорційна квадрату енергії. Це призводить до того, що траєкторії поблизу поверхні є більш спрямленими й електрони глибше проникають у товщу матеріалу мішені. Швидкість втрати енергії обернено пропорційна енергії пучка. Тому, маючи більшу енергію, електрони можуть глибше проникати у тверде тіло.
Розрахунки методом Монте-Карло показують, що розмір області взаємодії істотним чином залежить від кута падіння електронного пучка на мішень. Рисунок 1.7 дає можливість зрозуміти, що таке кут падіння та кут нахилу пучка.
Як видно з рисунка 1.8, зі збільшенням кута нахилу Q лінійні розміри області взаємодії (R) зменшуються. Така поведінка пов’язана з більшою ймовірністю розсіювання електронів за напрямом первинного руху. При нормальному падінні (Q = 0°) тенденція до розсіювання електронів вперед за напрямом руху примушує їх рухатись у товщу матеріалу.
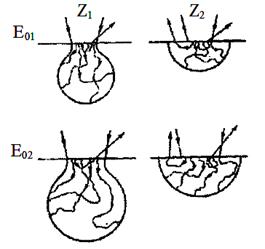
Рисунок 1.6 – Вплив атомного номера мішені та енергії пучка на форму та розмір області взаємодії [1]: Z1<<Z2 , E01<<E02
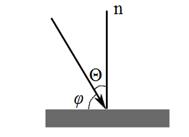
Рисунок 1.7 – Графічне пояснення термінів “кут падіння”(φ) та “кут нахилу”(Θ)
При зміні кута нахилу вищезгадана тенденція зберігається, що призводить до меншого проникнення електронів у мішень.
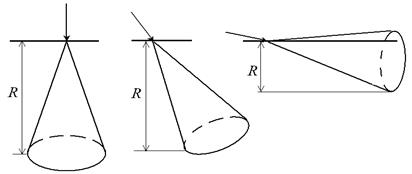
Рисунок 1.8 – До пояснення причини зменшення розміру області взаємодії зі збільшенням кута нахилу
Для пучка, що нахилений до поверхні, область взаємодії R виражається співвідношенням
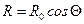 , (1.7)
, (1.7)
де R0 – розмір області взаємодії при нормальному падінні пучка.
При нормальному падінні пучка на мішень, яка має шорстку поверхню, кут нахилу “регулюють” нерівності на поверхні, що, у свою чергу, призводить до різного виходу відбитих електронів та обумовлює контраст на зображенні.
Розглянемо ще одне ключове поняття, що пов’язане з областю взаємодії, – довжина пробігу електрона.
Довжиною пробігу електрона (R) називають відстань, яку він проходить у мішені від точки падіння до точки, де його енергія зрівнюється з енергією вільних електронів у кристалі.
Існує кілька підходів до визначення довжини пробігу. Найбільшого поширення набули означення Бете (RБ) та Канайє-Окаяме (Rко).
Довжина пробігу згідно з Бете визначається за таким співвідношенням:
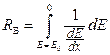 , (1.8)
, (1.8)
де 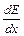 – швидкість втрати енергії (див. (1.4)).
– швидкість втрати енергії (див. (1.4)).
Якщо у співвідношення (1.8) підставити швидкість втрати енергії, то можна визначити довжину пробігу. Потрібно відмітити, що інтеграл у співвідношенні (1.8) має вигляд 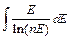 (такі інтеграли розраховуються методом чисельного інтегрування).
(такі інтеграли розраховуються методом чисельного інтегрування).
Швидкість втрати енергії обернено пропорційна густині матеріалу мішені. З цієї причини часто користуються так званою масовою довжиною пробігу
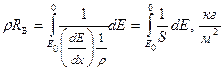 . (1.9)
. (1.9)
Довжина пробігу збільшується зі зростанням енергії електронного пучка і падає при збільшенні атомного номера мішені. Вона зростає при збільшенні атомного номера внаслідок збільшення густини матеріалу мішені.
Аналіз показує, що довжина пробігу згідно з Бете – це середня відстань, яку проходить електрон упродовж траєкторії. Але оскільки при пружній взаємодії відбувається неодноразова зміна напряму руху упродовж траєкторії, то реальні траєкторії сильно відрізняються від прямої лінії. Таким чином, довжина пробігу згідно з Бете є більшою, ніж максимальний розмір області взаємодії.
Довжина пробігу згідно з Канайє-Окаямою. Рядом дослідників було розглянуто питання про вплив пружного та непружного розсіювання на довжину пробігу електрона і було зроблено висновок, що емпіричний вираз, запропонований японськими вченими Канайє та Окаямою, який має вигляд
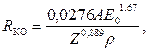 (1.10)
(1.10)
дає більш точне значення для розміру області взаємодії, ніж (1.8).
У даному співвідношенні RКО виражається в мкм, енергія – в кеВ, густина – в г/см3, а атомна маса – в г/моль. Ця довжина може бути інтерпретована як радіус напівсфери з центром у точці падіння, яка огинає кінцеві точки траєкторії електронів.
Таблиця 1.1 ілюструє значення розрахункових та експериментальних величин довжин пробігу для деяких матеріалів. Експериментальні величини (практичний та максимальний пробіг) були отримані для плівок шляхом визначення частки електронів, які пройшли зразок. Практична довжина пробігу може бути розглянута як розмір області взаємодії з великою густиною траєкторій електронів. Максимальний пробіг визначає розмір області взаємодії по лінії, що обмежує всі траєкторії.
Аналіз наведених у таблиці даних дозволяє зробити висновки:
– зі збільшенням енергії пучка величина довжини пробігу збільшується;
– збільшення атомного номера (густини) матеріалу мішені призводить до зменшення довжини пробігу;
Таблиця 1.1 – Порівняння різних значень довжин пробігу у мікрометрах [2]
| Мішень | Енергія пучка, кеВ | |||
| Al розрахунок: згідно з Бете згідно з Канайє-Окаямою експеримент: максимальний пробіг практичний пробіг | 0,56 0,41 0,48 0,33 | 1,80 1,32 1,10 0,85 | 6,04 4,20 — — | 12,3 8,30 — — |
| Cu розрахунок: згідно з Бете згідно з Канайє-Окаямою експеримент: максимальний пробіг практичний пробіг | 0,23 0,15 0,18 0,11 | 0,71 0,46 0,47 0,34 | 2,29 1,47 — — | 4,64 2,89 — — |
| Au розрахунок: згідно з Бете згідно з Канайє-Окаямою експеримент: максимальний пробіг практичний пробіг | 0,20 0,085 0,080 0,05 | 0,55 0,27 0,22 0,15 | 1,66 0,86 — — | 3,18 1,70 — — |
– розрахункові значення з використанням співвідношення Канайє-Окаями краще збігаються з експериментальною величиною максимальної довжини пробігу;
– довжина пробігу згідно з Бете менше збігається у тих випадках, коли пружне розсіювання має більшу ймовірність (великий атомний номер або низька енергія пучка);
– довжина пробігу, визначена за співвідношенням Бете, більша (до 50%) від розрахованої за формулою Канайє-Окаями.
3 Відбиті електрони
Дата добавления: 2015-05-26; просмотров: 1765;
