Максимизация прибыли фирмой-монополистом

Для решения задачи максимизации прибыли, в отличие от рынка совершенной конкуренции, где необходимо найти только оптимальный объем выпуска Q*, фирма - монополист должна выбрать оптимальную комбинацию (P*; Q*).

В микроэкономической теории выбор оптимальной комбинации (P*; Q*) фирма начинает с поиска Q*, в действительности чаще всего с поиска Р*.

Нахождение оптимального объема выпуска Q*.

Правило максимизации прибыли на рынке монополии такое же, как и на рынке совершенной конкуренции, только предельная выручка не равняется цене, а меньше ее:

MR = MC < P

При этом возможны такие же соотношения предельной выручки и цены товара:

1. MR > MC → произ-во добавочной единицы прибыльно (МП – предельная прибыль > 0 → есть стимулы к расширению производства

2. MR < MC → произ-во добавочной единицы убыточно (МП < 0 → расширение производства невозможно

3. MR = MC → условие максимизации прибыли, когда отсутствуют стимулы к расширению произ-ва (МП = 0) → оптимальный объем выпуска Q* найден

Нахождение оптимальной Р*.

После нахождения оптимального объема выпуска необходимо найти оптимальную цену двумя способами:

1. путем подставления значения оптимального Q* в функцию спроса, если она известна ( );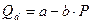

2. путем подставления предельных затрат МС в формулу ,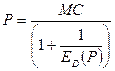

выведенную из формулы, связывающей предельную выручку с ценовой эластичностью спроса. Данной формулой можно воспользоваться при условии, что известен коэффициент ценовой эластичности спроса.

Графически поиск оптимальной комбинации (P*; Q*) можно представить следующим образом (рис. 44):

Рис. 44.Максимизация прибыли фирмой-монополистом

Точка пересечения линии MR и кривой MC укажет оптимальный объем выпуска Q*. Оптимальная цена Р* будет определяться высотой кривой спроса в точке, соответствующей оптимальному объему выпуска.