Метод симметричных составляющих. Метод симметричных составляющих базируется на математической теории многофазных электрических систем при неодинаковых условиях работы фаз.
Метод симметричных составляющих базируется на математической теории многофазных электрических систем при неодинаковых условиях работы фаз.
Сформулируем основные положения метода симметричных составляющих.
1. Любую несимметричную систему токов можно разложить на три симметричные, называемые системами прямой, обратной и нулевой последовательностей. Эти системы получили название «симметричные составляющие». Предполагается, что они одновременно циркулируют в рассматриваемой сети в несимметрично режиме. Симметричная система токов прямой последовательное! (рис. 5.1, а) представляет собой три одинаковых по величине вектора, расположенных под углом 120°, вращающихся против часовой стрелки так, что соблюдается нормальное чередование фаз А - В -С. Соотношения между фазными значениями устанавливаются с помощью оператора
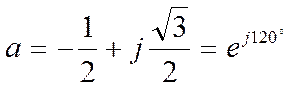
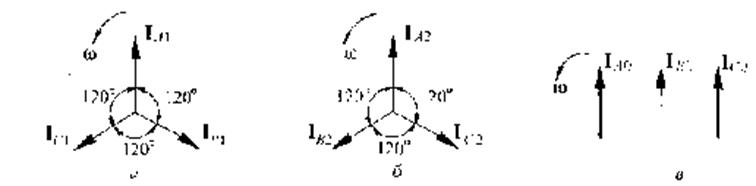
| Рис, 5.1. Система токов прямом (а) обратной (б) и нулевой (в) последовательностей |
Этот вектор единичной длины имеет аргумент, равный 120°. Если некоторый вектор, например  , умножусь на а, то это означает повернуть
, умножусь на а, то это означает повернуть  на 120° против часовой стрелки. С помощь вектора а можно выразить токи фаз В и С через ток фазы А:
на 120° против часовой стрелки. С помощь вектора а можно выразить токи фаз В и С через ток фазы А:
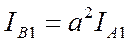 ,
, 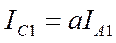
Симметричная система токов обратной последовательности (рис. 5.1, б) представляет собой три одинаковых по величине вектора, расположенных под углом 120° и вращающихся против часовой стрелки так, что соблюдается обратное чередование фаз А — С— В, При этом токи фаз В и С связаны с током фазы А следующим образом:
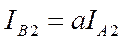 ,
, 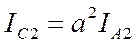 .
.
Симметричная система токов нулевой последовательности (рис. 5.1, в) существенно отличается от прямой и обратной. Oна представляет собой систему трех переменных токов, совпадающих по фазе и имеющих одинаковую амплитуду. Эти токи являются, по существу, разветвлением однофазного тока, для которого три провода трехфазной цепи составляют один прямой провод, а обратным служит земля или четвертый (нулевой) провод. Появление токов нулевой последовательности в сети означает возникновение в ней несимметричного замыкания на землю. Рассматриваемая несимметричная система токов допускает только одно разложение на симметричные составляющие. Действительно, представив ток каждой фазы через его симметричные составляющие, получим
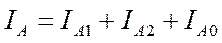 ,
,
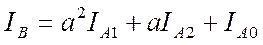 , (1)
, (1)
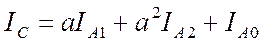 .
.
Если 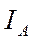 ,
, 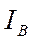 ,
, 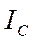 заданы, то искомыми являются три величины
заданы, то искомыми являются три величины
 ,
, 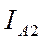 ,
,  . Они определяются тремя линейными уравнениями, которые допускают только одно решение:
. Они определяются тремя линейными уравнениями, которые допускают только одно решение:
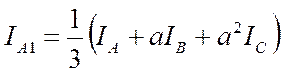 , (2)
, (2)
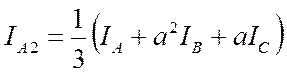 , (3)
, (3)
 . (4)
. (4)
Все соотношения дли симметричных составляющих токов справедливы и для напряжений.
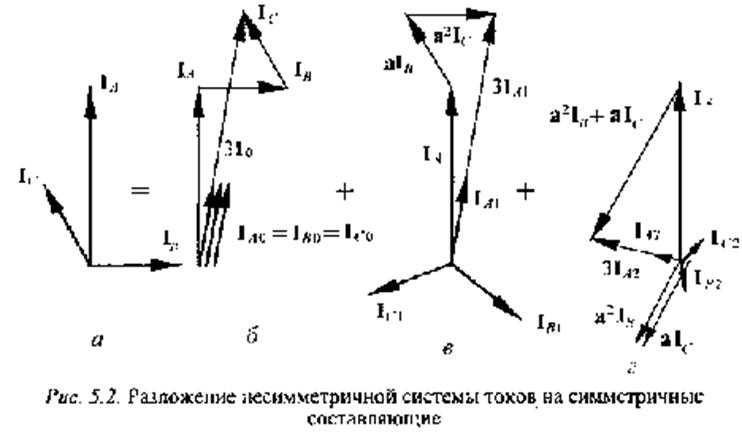
Рассмотрим разложение на составляющие несимметричной системы токов (рис. 5.2, а). С помощью геометрических построений, соответствующих выражениям (2)-(4), найдем ток нулевой, прямой и обратной последовательностей (рис. 5.2, б-г). Если сложить симметричные составляющие в соответствии с выражениями (1), то получим исходную систему.
 2. В трехфазной цепи в месте КЗ наряду с напряжениями прямой последовательности возникают напряжения обратной и ну левой последовательности. В ветвях схемы вместе с токами прямой последовательности начинают циркулировать токи обратной и нулевой последовательностей.
2. В трехфазной цепи в месте КЗ наряду с напряжениями прямой последовательности возникают напряжения обратной и ну левой последовательности. В ветвях схемы вместе с токами прямой последовательности начинают циркулировать токи обратной и нулевой последовательностей.
Для иллюстрации этого положения рассмотрим схему электрической системы, показанную на рис. 5.3. За положительное направление токов примем направление слева направо и допустим, что картина распределения имеет вид, показанный на рисунке. Тогда для участка 1
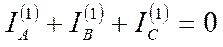 ,
, 
для участка 2
 ,
,
для участка 3
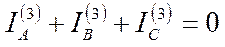 .
.
Из этих соотношений видно, что ток нулевой последовательности, определяемый по выражению (4), циркулирует только на участке 2.
Для участков 1 и 2 можно записать следующие соотношения:
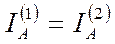 ,
, 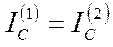 ,
,
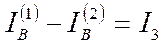 или
или 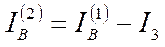 ,
,
где IЗ — ток в земле. Отсюда
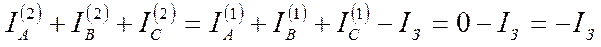
 Токи нулевой последовательности участка 2 с учетом (4) будут определены по формуле
Токи нулевой последовательности участка 2 с учетом (4) будут определены по формуле
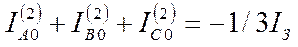
Схема циркуляции токов нулевой последовательности показан на рис. 5.4. Для этой схемы необходимы два допущения; а) ток земле составляет с токами нулевой последовательности проводе замкнутый контур; б) в точке КЗ не один, а все три провода соединены с землей.

 Таким образом, для тогочтобы получить физическую картину циркуляции токов нулевой последовательности, необходимо в провода, соединяющие фазы А, В, С с землей, включить источники напряжении нулевой последовательности так, как это указано на рис. 5.5.
Таким образом, для тогочтобы получить физическую картину циркуляции токов нулевой последовательности, необходимо в провода, соединяющие фазы А, В, С с землей, включить источники напряжении нулевой последовательности так, как это указано на рис. 5.5.
Все эти допущения являются необходимым следствием отделения системы токов нулевой последовательности от системы токов прямой и обратной последовательностей. Если прямую и обратную последовательности рассматривать отдельно, то придется и в отношении их сделать аналогичные допущения с той лишь разницей, что теперь относительно земли в каждую фазу необходимо вместо напряжений 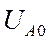 ,
, 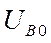 ,
, 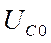 включить напряжения
включить напряжения 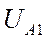 ,
, 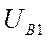 ,
,  или
или 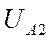 ,
, 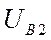 ,
, 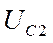 , представляющие собой симметричные звезды векторов.
, представляющие собой симметричные звезды векторов.
3. В симметричных электрических системах токи и напряжения схем отдельных последовательностей могут рассматриваться независимо друг от друга и быть связаны между собой законами Ома и Кирхгофа.
Если какой-либо элемент цепи симметричен и при протекании по нему токов I1, I2, I0 обладает некоторыми сопротивлениями Z1, Z2, Z0, то симметричные составляющие падения напряжения в этом элементе будут равны
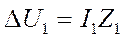 ,
, 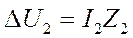 ,
, 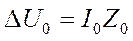 . (5)
. (5)
Комплексная форма уравнений (5) справедлива не только для стационарного режима, но и для переходного, так как токи и напряжения при переходном процессе можно представить проекция ми вращающихся векторов на соответствующую ось. При этом дифференциальным уравнениям, связывающим комплексные значения, отвечают операторные уравнения, которые при нулевых начальных условиях по своей структуре аналогичны уравнениям стационарного режима, записанным в комплексной форме.
Уравнения второго закона Кирхгофа для любого КЗ каждой последовательности могут быть записаны в виде
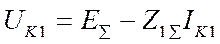 (6)
(6)
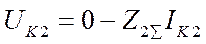 (7)
(7)
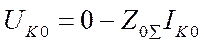 (8)
(8)
где UK1, UK2, UK0, IK1, IK2, IK0 - симметричные составляющие напряжения и тока в месте КЗ; 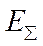 - результирующая ЭДС относительно точки КЗ;
- результирующая ЭДС относительно точки КЗ; 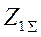 ,
, 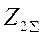 ,
, 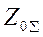 - результирующие сопротивления схем соответствующих последовательностей относительна точки КЗ.
- результирующие сопротивления схем соответствующих последовательностей относительна точки КЗ.
Запись уравнений второго закона Кирхгофа вызывает необходимость сформулировать следующее положение метода симметричных составляющих.
4. Элементы трехфазной сети для токов прямой, обратной и нулевой последовательностей имеют неодинаковые сопротивления. ЭДС генераторов симметричны, т.е. не содержат обратной и нулевой составляющих. Отсюда следует, что: а) в электрически системах существуют только ЭДС прямой последовательное б) токи обратной и пулевой последовательностей определяют» только напряжениями в точке КЗ.
5. Между системами трех симметричных составляющих всегда существует связь, задаваемая условиями короткого замыкания. Эта связь легко устанавливается путем перевода граничных условий короткого замыкания, заданных через действительные токи и напряжения, в условия, заданные через симметричные составляющие.
3.5. При расчетах токов КЗ допускается:
1) максимально упрощать и эквивалентировать всю внешнюю сеть по отношению к месту КЗ и индивидуально учитывать только автономные источники электроэнергии и электродвигатели, непосредственно примыкающие к месту КЗ;
2) не учитывать ток намагничивания трансформаторов;
3) не учитывать насыщение магнитных систем электрических машин;
4) принимать коэффициенты трансформации трансформаторов равными отношению средних номинальных напряжений тех ступеней напряжения сетей, которые связывают трансформаторы. При этом следует использовать следующую шкалу средних номинальных напряжений: 515,340,230,154,115,37; 24; 20; 15,75; 13,8; 10,5; 6,3; 3,15; 0,69; 0,525; 0,4; 0,23 кВ;
5) не учитывать влияния асинхронных электродвигателей, если их суммарный номинальный ток не превышает 1,0 % начального значения периодической составляющей тока в месте КЗ, рассчитанного без учета электродвигателей.
6) не учитывать ток ХХ линий или емкостную проводимость линий считать равной нулю- это допущение действует ля ВЛ до 220 кВ, для КЛ- до 35 кВ.
7) В сетях до 1 кВ не учит. акт. сопр.
8) не учит. сдвиг фаз м/у векторами ЭДС источников, т.е. все ЭДС совпадают по фазе.
9 ) не учитывать межсистемные связи, выполненные с помощью электропередачи (вставки) постоянного тока;
Помимо этих допущений неявно подразумевается:
1. Сохранение симметрии в 3-фазной системе
2. Отсутствие насыщения – линейность - можно применять принцип суперпозиции
3. Отсут. качаний СМ (скорость СМ=const)
Дата добавления: 2015-05-21; просмотров: 1078;
