Построение аксонометрических проекций

5.5.1. Общие положения. Ортогональные проекции объекта дают полное представление о его форме и размерах. Однако очевидным недостатком таких изображений является их малая наглядность – образная форма слагается из нескольких изображений, выполненных на разных плоскостях проекций. Только в результате опыта развивается умение представлять себе форму объекта – «читать чертежи».

Затруднения при чтении изображений в ортогональных проекциях обусловили возникновение ещё одного метода, который должен был объединить простоту и точность ортогональных проекций с наглядностью изображения,– метода аксонометрических проекций.

Аксонометрической проекциейназывают наглядное изображение, получаемое в результате параллельного проецирования предмета вместе с осями прямоугольных координат, к которым он отнесен в пространстве, на какую-либо плоскость.

Правила выполнения аксонометрических проекций устанавливаются ГОСТ 2.317-69.

Аксонометрия (от греческого axon – ось, metreo – мерю) – процесс построения, основанный на воспроизведении размеров предмета по направлениям трёх его осей – длины, ширины, высоты. В результате получается объёмное изображение, воспринимаемое как осязаемая вещь (рис. 56б), в отличие от нескольких плоских изображений, не дающих образной формы предмета (рис. 56а).

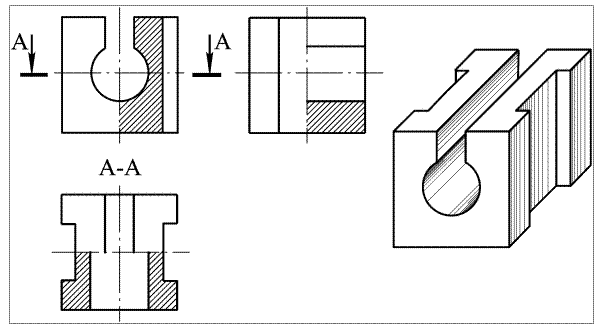
а б

Рис. 56. Наглядное изображение аксонометрии

В практической работе аксонометрические изображения применяются для различных целей, поэтому были созданы различные их виды. Общим для всех видов аксонометрии является то, что за основу изображения любого предмета принимается то или иное расположение осей OX, OY, OZ, по направлению которых определяют размеры предмета – длину, ширину, высоту.

В зависимости от направления проецирующих лучей по отношению к картинной плоскости, аксонометрические проекции подразделяются на:

а) прямоугольные– проецирующие лучи перпендикулярны картинной плоскости (рис. 57а);

б) косоугольные– проецирующие лучи наклонены к картинной пло­скости (рис. 57б).

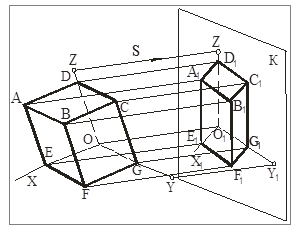
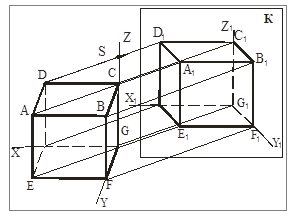
а б

Рис. 57. Прямоугольная и косоугольная аксонометрия

В зависимости от положения предмета и осей координат относительно плоскостей проекций, а также в зависимости от направления проециро­вания единицы измерения проецируются в общем случае с искажением. Искажаются и размеры проецируемых предметов.

Отношение длины аксонометрической единицы к ее истинной вели­чине называют коэффициентом искажения для данной оси.

Аксонометрические проекции называют: изометрическими, если коэф­фициенты искажения по всем осям равны (х= у= z); диметрическими, если коэффициенты искажения равны по двум осям(x=z);триметрическими, если коэффициенты искажения различны.

Для аксонометрических изображений предметов применяют пять видов аксонометрических проекций, установленных ГОСТ 2.317 – 69:

прямоугольные – изометрические и диметрические;

косоугольные– фронтальные диметрические, фронтальныеизомет­рические, горизонтальные изометрические.

Имея ортогональные проекции любого предмета, можно построить его аксонометрическое изображение.

Всегда необходимо выбирать из всех видов лучший вид данного изо­бражения – тот, который обеспечивает хорошую наглядность и простоту построения аксонометрии.

5.5.2. Общий порядок построения. Общий порядок построения любого вида аксонометрии сводится к следующему:

а) выбирают оси координат на ортогональной проекции детали;

б) строят эти оси в аксонометрической проекции;

в) строят аксонометрию полного изображения предмета, а затем и его элементов;

г) наносят контуры сечения детали и убирают изображение отсечённой части;

д) обводят оставшуюся часть и проставляют размеры.

5.5.3. Прямоугольная изометрическая проекция. Этот вид аксонометрической проекции широко распространён благо­даря хорошей наглядности изображений и простоте построений. В пря­моугольной изометрии аксонометрические оси OX, OY, OZ расположены под углами 120⁰ одна к другой. Ось OZ вертикальна. Оси OX и OY удобно строить, откладывая с помощью угольника от горизонтали углы 30⁰. Поло­жение осей можно также определить, отложив от начала координат в обе стороны по пять произвольных равных единиц. Через пятые деления про­водят вниз вертикальные линии и откладывают на них по 3 такие же еди­ницы. Действительные коэффициенты искажения по осям равны 0,82. Что­бы упростить построение, применяют приведённый коэффициент, равный 1. В этом случае при построении аксонометрических изображений измере­ния предметов, параллельные направлениям аксонометрических осей, от­кладывают без сокращений. Расположение аксонометрических осей и по­строение прямоугольной изометрии куба, в видимые грани которого впи­саны окружности, показаны на рис. 58, а, б.

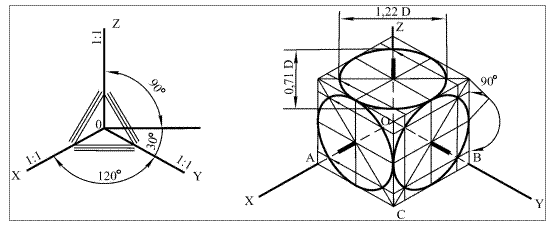
а б

Рис. 58. Расположение осей прямоугольной изометрии

Окружности, вписанные в прямоугольную изометрию квадратов – трех видимых граней куба, – представляют собой эллипсы. Большая ось эллип­са равна 1,22 D, а малая – 0,71 D, где D– диаметр изображаемой окруж­ности. Большие оси эллипсов перпендикулярны соответствующим аксоно­метрическим осям, а малые оси совпадают с этими осями и с направле­нием, перпендикулярным плоскости грани куба (на рис. 58б – утолщенные штрихи).

При построении прямоугольной аксонометрии окружностей, лежащих в координатных или им параллельных плоскостях, руководствуются пра­вилом: большая ось эллипса перпендикулярна той координатной оси, ко­торая отсутствует в плоскости окружности.

Зная размеры осей эллипса и проекции диаметров, параллельных координатным осям, можно построить эллипс по всем точкам, соединяя их с помощью лекала.

Чтобы упростить построения, рекомендуется заменять эллипсы овалами, оси которых равны осям эллипса.

Построение овала по четырём точкам – концам сопряжённых диамет­ров эллипса, расположенных на аксонометрических осях, показано на рис. 59.

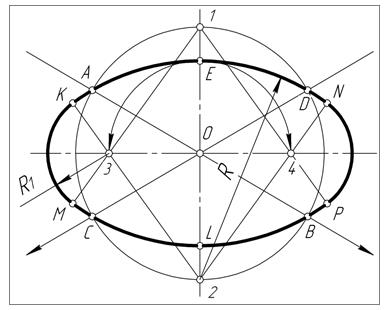
Рис. 59. Построение овала

Через точкуО пересечения сопряжённых диаметров эллипса проводят горизонтальную и вертикальную прямые и из неё описывают окружность радиусом, равным половине сопряжённых диаметров АВ=СД. Эта окружность пересечёт вертикальную линию в точках 1 и 2 (центры двух дуг). Из точек 1, 2 проводят дуги окружностей радиусом R=2-А (2-D) или R=1-C (1-B). Радиусом ОЕ делают засечки на горизонтальной прямой и получают еще два центра сопрягаемых дуг 3 и 4. Далее соединяют центры 1 и 2 с центрами 3 и 4 линиями, которые в пересечении с дугами радиусомR дают точки сопряжений K, N, P, M. Крайние дуги проводят из центров 3 и 4 радиусом R₁=3-М (4-N).

Построение прямоугольной изометрии детали, заданной её проекция­ми, производят в следующем порядке (рис. 60, 61).

1. Выбирают оси координат X, Y, Z на ортогональных проекциях.

2. Строят аксонометрические оси в изометрии.

3. Строят основание детали – параллелепипед. Для этого от начала координат по оси Х откладывают отрезки ОА и ОВ, соответственно равные отрезкам О₁А₁ и О₁В₁, взятым с горизонтальной проекции детали, и получают точкиА и В, через которые проводят прямые, параллельные оси Y, и откладывают отрезки, равные половине ширины параллелепипеда.

Получают точки C, D, J, V, которые являются изометрическими проек­циями вершин нижнего прямоугольника, и соединяют их прямыми, па­раллельными оси Х. От начала координат О по оси Z откладывают отрезок ОО₁, равный высоте параллелепипеда О₂О₂´; через точку О₁ проводят оси Х₁, Y₁ и строят изометрию верхнего прямоугольника. Вершины прямо­угольников соединяют прямыми, параллельными оси Z.

4. Строят аксонометрию цилиндра. По оси Z от О₁ откладывают отре­зок О₁О₂, равный отрезку О₂´О₂´´, т.е. высоте цилиндра, и через точку О₂ проводят оси X₂,Y₂. Верхнее и нижнее основания цилиндра являются окружностями, расположенными в горизонтальных плоскостях X₁O₁Y₁ и X₂O₂Y₂; строят их аксонометрические изображения – эллипсы. Очерковые образующие цилиндра проводят касательно к обоим эллипсам (парал­лельно оси Z). Построение эллипсов для цилиндрического отверстия вы­полняют аналогично.

5. Строят изометрическое изображение ребра жёсткости. От точки О₁ по оси Х₁ откладывают отрезок О₁Е=О₁Е₁. Через точку Е проводят прямую, параллельную оси Y, и откладывают в обе стороны отрезки, равные половине ширины ребра Е₁К₁ и Е₁F₁. Из полученных точек К, Е, F параллельно оси Х₁ проводят прямые до встречи с эллипсом (точки Р, N, М). Далее проводят прямые, параллельные оси Z (линии пересечения плоскостей ребра с поверхностью цилиндра), и на них откладывают отрезки РТ, MQ и NS, равные отрезкам Р₂Т₂, M₂Q₂, и N₂S₂. Точки Q, S, T соединяют и обводят по лекалу, а точки К, Т и F, Q соединяют прямыми.

6. Строят вырез части заданной детали, для чего проводят две секущие плоскости: одну через оси Z и Х, а другую – через оси Z и Y.

Первая секущая плоскость разрежет нижний прямоугольник паралле­лепипеда по оси Х (отрезок ОА), верхний – по оси Х₁, а ребро – по линиям EN и ES, цилиндры – по образующим, верхнее основание цилиндра – по оси Х₂.

Аналогично вторая секущая плоскость разрежет верхний и нижний прямоугольники по осям Y и Y₁, а цилиндры – по образующим, верхнее основание цилиндра – по оси Y₂.

Плоские фигуры, полученные от сечения, заштриховываются. Для определения направления штриховки необходимо на аксонометрических осях отложить от начала координат равные отрезки, а затем концы их со­единить.

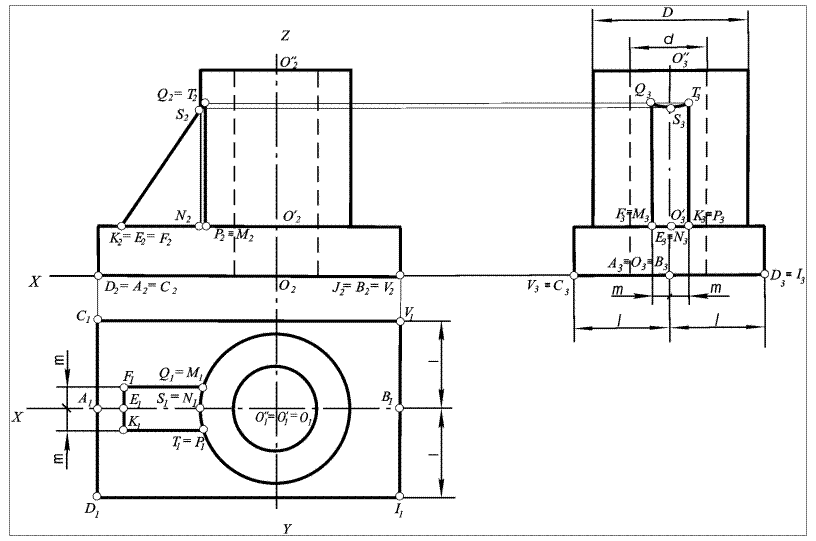
Рис. 60. Построение трех проекций детали

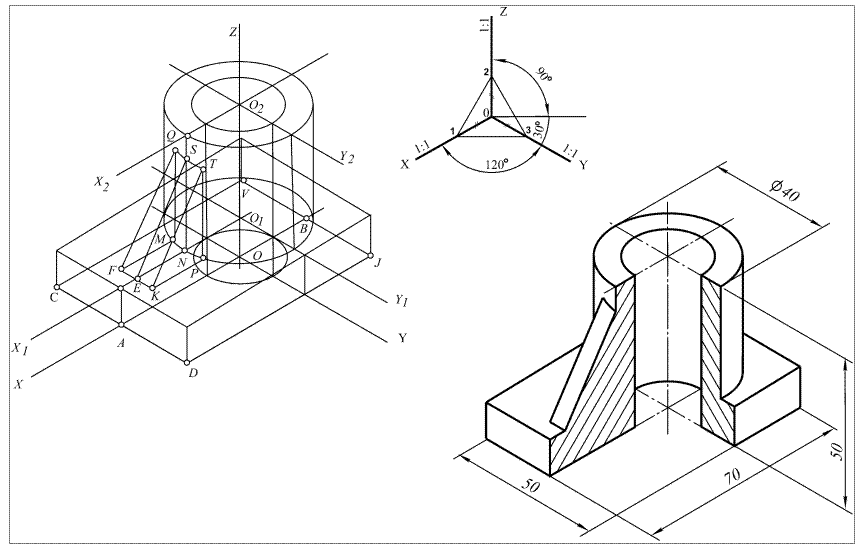
Рис. 61. Выполнение прямоугольной изометрии детали

Линии штриховки для сечения, расположенного в плоскости XOZ, будут параллельны отрезку 1-2, а для сечения, лежащего в плоскости ZOY, – параллельны отрезку 2-3. Удаляют все невидимые линии и обводят контурные линии. Изометрическую проекцию применяют в тех случаях, когда необходимо построить окружности в двух или трёх плоскостях, параллельных координатным осям.

5.5.4. Прямоугольная диметрическая проекция. Аксонометрические изображения, построенные прямоугольной димет­рии, обладают наилучшей наглядностью, однако построение изображений сложнее, чем в изометрии. Расположение аксонометрических осей в диметрии следующее: ось OZ направлена вертикально, а оси OХ и OY составляют с горизонтальной линией, проведённой через начало координат (точка О), углы, соответственно, 7º10´ и 41º25´. Положение осей можно также определить, отложив от начала координат в обе стороны по восемь равных отрезков; через восьмые деления проводят вниз линии и на левой вертикали откладывают один отрезок, а на правой – по семь отрезков. Соединив полученные точки с началом координат, определяют направление осей ОХ и ОУ (рис. 62).

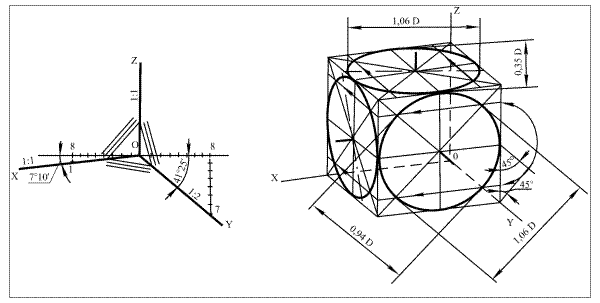
а б

Рис. 62. Расположение осей в прямоугольной диметрии

Коэффициенты искажения по осям ОХ, OZ равны 0,94, а по оси ОY– 0,47. Для упрощения в практике пользуются приведёнными коэффициентами искажения: по осям OX и OZ коэффициент равен 1, по оси ОY– 0,5.

Построение прямоугольной диметрии куба с окружностями, вписанными в три видимые его грани показано на рис. 62б. Окружности, вписанные в грани, представляют собой эллипсы двух видов. Оси эллипса, расположенного в грани, которая параллельна координатной плоскости XOZ, равны: большая ось – 1,06 D; малая – 0,94 D, где D– диаметр окружности, вписанной в грань куба. В двух других эллипсах большие оси равны 1,06 D, а малые – 0,35 D.

Для упрощения построений можно заменить эллипсы овалами. На рис. 63 даны приёмы построения четырех центровых овалов, заменяющих эллипсы. Овал в передней грани куба (ромба) строится следующим образом. Из середины каждой стороны ромба (рис. 63а) проводят перпендикуляры до пересечения с диагоналями. Полученные точки 1-2-3-4 будут являться центрами сопрягающих дуг. Точки сопряжений дуг находятся посредине сторон ромба. Построение можно выполнить и другим способом. Из середин вертикальных сторон (точки N и M) проводят горизонтальные прямые линии до пересечения с диагоналями ромба. Точки пересечения будут искомыми центрами. Из центров 4 и 2 проводят дуги радиусом R, а из центров 3 и 1– радиусом R₁.

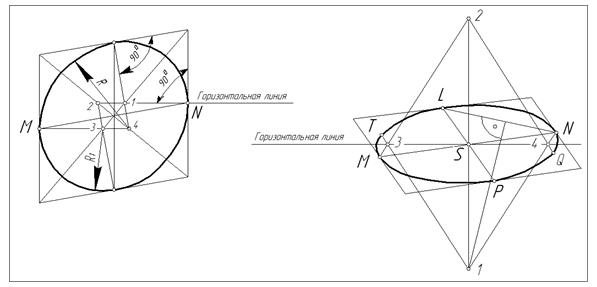
а б

Рис. 63. Построение окружности в прямоугольной диметрии

Овал, заменяющий два других эллипса, выполняют следующим образом (рис. 63б). Прямые LP и MN, проведенные через середины противоположных сторон параллелограмма, пересекаются в точке S. Через точку S проводят горизонтальную и вертикальную линии. Прямую LN, соединяющую середины смежных сторон параллелограмма, делят пополам, и через ее середину проводят перпендикуляр до пересечения его с вертикальной линией в точке 1.

на вертикальной прямой откладывают отрезок S-2 = S-1.Прямые2-М и 1-N пересекают горизонтальную прямую в точках 3 и 4. Полученные точки 1, 2, 3 и 4 будут центрами овала. Прямые 1-3 и 2-4 определяют точки сопряжения T и Q.

из центров 1 и 2 описывают дуги окружностей TLN и QPM, а из центров 3 и 4– дуги MT и NQ. Принцип построения прямоугольной диметрии детали (рис. 64) аналогичен принципу построения прямоугольной изометрии, приведённой на рис. 61.

Выбирая тот или иной вид прямоугольной аксонометрической проекции, следует иметь в виду, что в прямоугольной изометрии поворот боковых сторон предмета получается одинаковым и поэтому изображение иногда оказывается не наглядным. Кроме того, часто диагональные в плане ребра предмета на изображении сливаются в одну линию (рис. 65б). Эти недостатки отсутствуют на изображениях, выполненных в прямоугольной диметрии (рис. 65в).

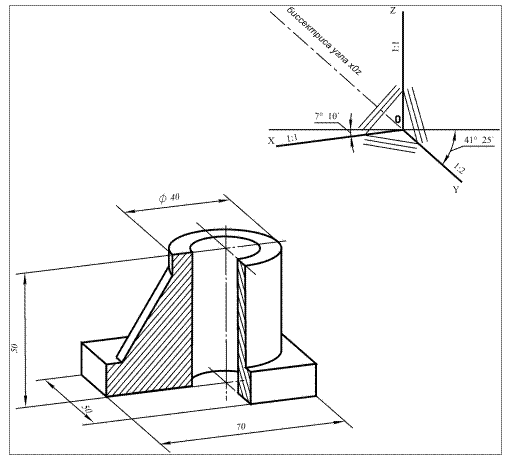
Рис. 64. Построение детали в прямоугольной диметрии

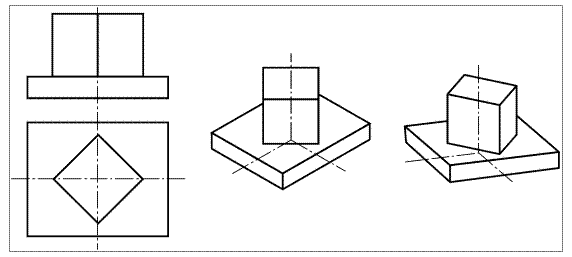
а б в

Рис. 65. Сравнение различных видов аксонометрии

5.5.5. Косоугольная фронтальная изометрическая проекция.

Аксонометрические оси располагаются следующим образом. Ось OZ - вертикальная, ось ОХ– горизонтальная, ось ОУ относительно горизон­тальной прямой расположена над углом 45⁰ (30⁰, 60⁰) (рис. 66а). По всем осям размеры откладывают без сокращений, в истинную величину. На рис. 66б показана фронтальная изометрия куба.

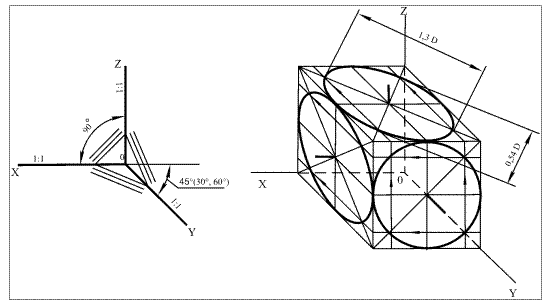
а б

Рис. 66. Построение косоугольной фронтальной изометрии

Окружности, расположенные в плоскостях, параллельных фронтальной плоскости, изображаются в натуральную величину. Окружности, расположенные в плоскостях, параллельных горизонтальной и профильной плоскостям, изображаются в виде эллипсов.

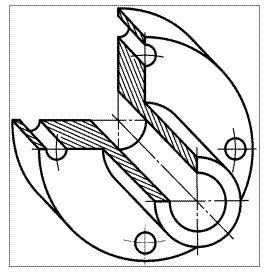
Рис. 67. Деталь в косоугольной фронтальной изометрии

Направление осей эллипсов совпадает с диагоналями граней куба. Для плоскостей ХОY и ZОY величина большой оси равна 1,3 D, а малой – 0,54 D (D– диаметр окружности).

Пример фронтальной изометрии детали приведён на рис. 67.