Уравнение изотермы химической реакции.

Предположим, в смеси идеальных газов протекает химическая реакция по уравнению

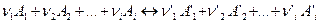
Допустим, что в момент приготовления реакционной смеси в ней присутствуют все реагирующие вещества. Обозначим исходные (неравновесные) относительные парциальные давления реагентов в системе через для того, чтобы отличать их от равновесных относительных парциальных давлений тех же реагентов.

В очередной раз воспользуемся уравнением (IV, 11):

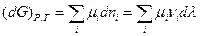
Разделив обе части уравнения на , получим:

(V,6)

Если смесь компонентов с неравновесными парциальными давлениями всех участников реакции имеет настолько большую массу, что изменение количества компонентов в результате одного пробега реакции практически не изменит их парциальных давлений, то в уравнении (V,6) можно заменить величину 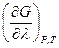равной ей величиной .

Положив (реакция совершила один пробег), с учетом (III, 46) получим:

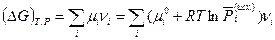(V,7)

Уравнение (V,7) преобразуем к виду

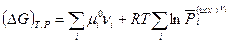
Так как (смотри (V,4)), то

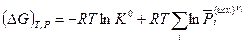(V,8)

В этом уравнении 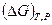- изменение энергии Гиббса системы при химическом превращении такого числа молей реагирующих веществ, которое соответствует стехиометрическому уравнению реакции. Величина 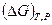называется изменением энергии Гиббса химической реакции. Уравнение (V,8) впервые было выведено Вант-Гоффом и называется уравнением изотермы реакции.

Ниже приводится развернутая форма уравнения (V,8):

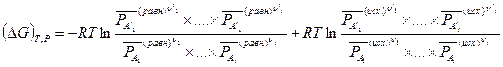
Следующая тождественная форма записи уравнения (V,8) является наиболее распространенной:

(V,9)

Уравнение (V,9) позволяет вычислить изменение энергии Гиббса, а также предсказать направление протекания реакции при заданных условиях, если известны относительные парциальные давления реагирующих веществ в момент их смешения и стандартная константа равновесия. Константа равновесия 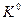может быть вычислена на основании равновесного состава реакционной смеси или по третьему закону термодинамики.

Итак, чтобы ответить на вопрос о возможности самопроизвольного протекания химической реакции в закрытой системе слева направо или справа налево, необходимо знать состав реакционной смеси в момент ее приготовления и стандартную константу равновесия при данной температуре.

Если в момент смешения относительные парциальные давления каждого реагента равны единице (все вещества вступают в реакцию в своих стандартных состояниях), то уравнение (V,9) запишется в виде:

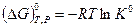(V,10)

Величина 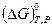- стандартное изменение энергии Гиббса химической реакции.

Смысл величин 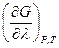и 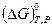можно уяснить с помощью следующей схемы. На рис.8 изображена в общей форме зависимость величины 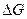от 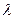при изотермическом переходе от исходных веществ (их суммарную энергию Гиббса обозначим 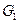) к продуктам реакции ( ). Величина может быть меньше величины , когда продукты реакции более устойчивы, чем смесь исходных веществ. Возможен и обратный случай.

Рис.8. Зависимость величины G от химической постоянной λ

В начальном состоянии парциальные давления продуктов реакции равны нулю, в конечном состоянии парциальные давления исходных веществ равны нулю. В равновесной смеси при условии

0 < λ < 1 производная 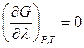и касательная к кривой параллельна оси абсцисс. Величина 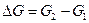и 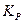, связанная со значением 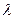, определяющим состояние равновесия, взаимно и однозначно определяют друг друга.

Чем больше величина отличается от величины , тем ближе положение равновесия к одной из границ диаграммы. Чем больше сближаются величины и , тем ближе положение равновесия к середине диаграммы. Конкретный вид кривой зависит от стехиометрического типа реакции и разности 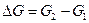, т.е., от индивидуальных свойств участников реакции.

В каждой точке кривой наклон касательной определяет значение 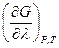в смеси данного состава. Стандартное изменение энергии Гиббса химической реакции равно .

Реальный химический процесс всегда протекает так, что энергия Гиббса изменяется по кривой в направлении к ее минимуму. При этом в зависимости от исходного состава смеси это изменение идет по правой или левой (по отношению к экстремуму) части кривой.